Домино

[wpoms.]

Домино представляет собой прямоугольник `1 times 2` или `2 times 1`. Диего хочет полностью покрыть доску `6 times 6` с помощью 18 домино. Определить наименьшее целое положительное число `k`, для которого Диего может разместить `k` домино на доске (без перекрытия) так, что остальная часть доски может быть покрыта оставшимися домино единственным способом.

@темы: Комбинаторика

---

вот такое вот задание...

[Nicas]

Найти уравнение кривой,проходящей через точку (2;3) и обладающую тем свойством,что отрезок любой её касательной,заключенный между координатными осями делится пополам в точке касания



Как эту задачку вобще делать?подскажите что нужно делать

@темы: Дифференциальные уравнения

---

Вычислить площадь части поверхности

[Brigantinna]

Прошу помощи.
Решила задачу, но сомневаюсь правильно ли.
Вычислить площадь части поверхности, уравнение которой задано в условии задач первым, вырезанной другими заданными поверхностями из нее.
`x^2+y^2+z^2=25` и `z=4`
Моё решение:

@темы: Кратные и криволинейные интегралы, Математический анализ

---

[Amicus Plato]

Каждый знает, что такое кривая, пока не изучит математику настолько, чтобы запутаться в бесчисленном количество всевозможных исключений. Феликс Клейн

Сегодня исполняется 164 года со дня рождения выдающегося немецкого математика и педагога Феликса Клейна.

Википедия.
Феликс Христиан Клейн (нем. Felix Christian Klein; 1849—1925) — немецкий математик и педагог. Член Берлинской академии наук (1913), иностранный член-корреспондент Петербургской академии наук (1895).

Биография
Феликс Клейн родился в Дюссельдорфе, в семье чиновника. Закончил гимназию в Дюссельдорфе, потом учился математике и физике в Боннском университете. Вначале планировал стать физиком. В это время Юлиус Плюккер заведовал отделением математики и экспериментальной физики в Бонне, и Клейн стал его ассистентом. Однако главным интересом Плюккера была геометрия. Под его руководством Клейн стал доктором в 1868 году.
1868: Плюккер умер. Клейн совершает поездку по Германии, знакомится с Клебшем и другими крупными математиками. Особенное влияние на него оказал Софус Ли.
1870: в самое неудачное время (назревает франко-прусская война) вместе с Ли приезжает в Париж, где знакомится с Дарбу и Жорданом. После начала войны возвращается в Германию, где чуть не становится жертвой спутника войны — эпидемии тифа.
1872: профессор Эрлангенского университета, по рекомендации Клебша. Публикует знаменитую «Эрлангенскую программу» и сразу приобретает общеевропейскую известность.
1875: профессор Высшей технической школы в Мюнхене. Женится на Анне Гегель, внучке знаменитого философа.
1876: совместно с Адольфом Майером становится главным редактором журнала «Mathematische Annalen».
1880: переходит в Лейпцигский университет.
1882—1884: серьёзная болезнь по причине переутомления. Клейн переориентирует свою гигантскую энергию на педагогическую и общественную работу.
1888: профессор Гёттингенского университета. Ведёт яркие, глубокие и содержательные факультативные курсы по самым разнообразным предметам, от теории чисел до технической механики. Слушатели его курсов приезжали со всех концов мира.
В начале XX века Клейн принял активное участие в реформе школьного образования, автор и инициатор ряда исследований состояния дел с преподаванием математики в разных странах.
Клейн способствовал созданию при Гёттингенском университете системы научно-исследовательских институтов для прикладных исследований в самых разных технических областях. Участвовал в издании полного собрания сочинений Гаусса и первой Математической энциклопедии. Представлял Гёттингенский университет в парламенте. Надо отметить, что с началом Первой мировой войны Клейн не участвовал в многочисленных тогда шовинистических акциях.
1924: широко отмечается 75-летие Клейна. В следующем году те же газеты опубликовали его некролог.

Раздел про его научную деятельность публиковать не буду. Вместо этого чуть-чуть расскажу про бутылку Клейна и приведу список литературы.

Бутылка Клейна
Бутылка Клейна — это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка); затем это название вернулось в таком виде в немецкий.
Чтобы построить модель бутылки Клейна, понадобится бутылка с двумя дополнительными отверстиями: в донышке и в стенке. Горлышко бутылки нужно вытянуть, изогнуть вниз, и продев его через отверстие в стенке, присоединить к отверстию на дне бутылки. Для настоящей бутылки Клейна в четырёхмерном пространстве отверстие в стенке не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве.

В отличие от обыкновенного стакана у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).
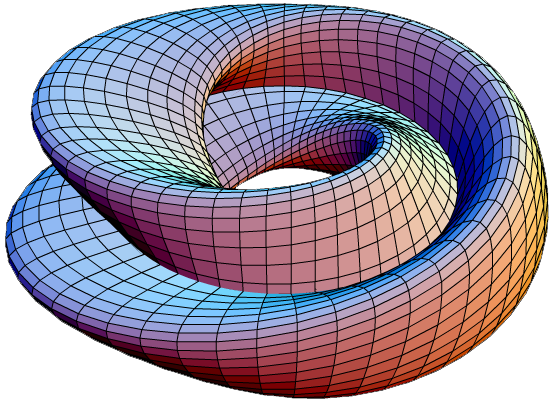
Бутылка Клейна, погруженная в трехмерное пространство:

Свойства

• Подобно ленте Мёбиуса, бутылка Клейна является двумерным дифференцируемым неориентируемым многообразием. В отличие от ленты Мёбиуса, бутылка Клейна является замкнутым многообразием, то есть компактным многообразием без края.
• Бутылка Клейна не может быть вложена (только погружена) в трёхмерное евклидово пространство `RR^3`, но вкладывается в `RR^4`.
• Бутылка Клейна может быть получена склеиванием двух лент Мёбиуса по краю. Однако в обычном трехмерном евклидовом пространстве `RR^3` сделать это, не создав самопересечения, невозможно.
• Хроматическое число поверхности равно 6.

Рассечения
При рассечении бутылки Клейна получается лента Мёбиуса.
Если разрезать бутылку Клейна пополам вдоль её оси симметрии, то результатом будет лента Мёбиуса, изображенная внизу (необходимо помнить, что изображенного пересечения на самом деле нет).

Реализация бутылки Клейна в виде восьмерки:

Стеклянная бутылка Клейна:

Больше картинок (и все очень хороши!) в английской Википедии: en.wikipedia.org/wiki/Klein_bottle

Ссылки на литературу.
1. Яглом И.М. Феликс Клейн и Софус Ли. 1977 libgen.info
2. Книги Ф. Клейна libgen.info:
Клейн Ф. Элементарная математика с точки зрения высшей том 1 1987
Клейн Ф. Элементарная математика с точки зрения высшей том 2 1987
Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени 1989
Клейн Ф. Высшая геометрия 2004
Клейн Ф. Неевклидова геометрия 1936
Клейн Ф. Лекции о развитии математики в XIX столетии часть 1 1937
Клейн Ф. Вопросы элементарной и высшей математики. Арифметика, алгебра и анализ Часть 1 1912

@темы: История математики, Люди

---

[Хероджин]

найти постоянные уравнения:
у'' + y' - 2y = cos x - 3 sin x
при
x=0 y=1
y'=2 x=0

Принцип решения более-менее ясен, но вот что-то никак не могу понять каким будет у-частичный-неоднородный.

@темы: Дифференциальные уравнения

---

[Amicus Plato]

Я принадлежу к тем крайне отчаянным кибернетикам, которые не видят никаких принципиальных ограничений в кибернетическом подходе к проблеме жизни и полагают, что можно анализировать жизнь во всей её полноте, в том числе и человеческое сознание, методами кибернетики. Продвижение в понимании механизма высшей нервной деятельности, включая и высшие проявления человеческого творчества, по-моему, ничего не убавляет в ценности и красоте творческих достижений человека. А. Н. Колмогоров

Сегодня исполняется 110 лет со дня рождения Андрея Николаевича Колмогорова.
Если честно, я даже в некоторой растерянности, потому что писать о нем очень непросто... Уж больно много всего нужно сказать... Поэтому, пожалуй, я ограничусь минимальными сведениями. И многими ссылками на всякие источники.

Википедия.
Андрей Николаевич Колмогоров (урождённый Катаев, 12 (25) апреля 1903, Тамбов — 20 октября 1987, Москва) — советский математик, один из крупнейших математиков ХХ века.
Колмогоров — один из основоположников современной теории вероятностей, им получены основополагающие результаты в топологии, геометрии, математической логике, классической механике, теории турбулентности, теории сложности алгоритмов, теории информации, теории функций, теории тригонометрических рядов, теории меры, теории приближения функций, теории множеств, теории дифференциальных уравнений, теории динамических систем, функциональном анализе и в ряде других областей математики и её приложений. Колмогоров также автор новаторских работ по философии, истории, методологии и преподаванию математики, известны его работы в статистической физике (в частности, уравнение Джонсона — Меля — Аврами — Колмогорова).

Профессор Московского государственного университета (с 1931), доктор физико-математических наук, академик Академии наук СССР (1939). Президент Московского математического общества (ММО) в 1964—1966 и 1974—1985.
Иностранный член Национальной академии наук США (1967), Лондонского королевского общества (1964), член Германской академии естествоиспытателей «Леопольдина» (1959), Французской (Парижской) академии наук (1968), почётный член Американской академии искусств и наук (1959), иностранный член Венгерской академии наук (1965), Польской академии наук (1956), Нидерландской королевской академии наук (1963), АН ГДР (1977), Академии наук Финляндии (1985), почетный член Румынской академии. Член Лондонского математического общества (1962), Индийского математического общества (1962), иностранный член Американского философского общества (1961). Колмогоров — почётный доктор Парижского университета (1955), Стокгольмского университета (1960), Индийского статистического института (англ.)русск. в Калькутте (1962).

А. Н. Колмогоров — основатель большой научной школы, среди его учеников: В. И. Арнольд, И. М. Гельфанд, В. М. Алексеев, Г. И. Баренблатт, А. А. Боровков, А. Г. Витушкин, Б. В. Гнеденко, Р. Л. Добрушин, Е. Б. Дынкин, А. И. Мальцев, М. Д. Миллионщиков, В. С. Михалевич, А. С. Монин, С. М. Никольский, А. М. Обухов, Ю. В. Прохоров, Я. Г. Синай, В. М. Тихомиров, Ю. Н. Тюрин, А. Н. Ширяев, В. А. Успенский, C. В. Фомин, А. М. Яглом и многие другие.

---

1. Статья в Википедии. (Статья очень большая и подробная. Там же в конце очень много ссылок на другие ресурсы)
2. Портал, посвященный А.Н. Колмогорову
3. В.И. Арнольд. Об А.Н. Колмогорове

---

4. А.Н. Колмогоров, Curriculum Vitae
5. А.Н. Колмогоров. О профеcсии математика
6. А.Н. Колмогоров. Математика – наука и профессия
7. Статьи А.Н. Колмогорова в журнале "Квант"

---

8. Колмогоров. Юбилейное издание в 3-х книгах Автор: Ширяев А.Н. (ред.-сост.) (eek.diary.ru)

@темы: История математики, Люди

---

Здравствуйте.Помогите с системой уравнений

[Nicas]

`{((dx)/(dt) = 4x + 6y),((dy)/(dt) = 4x + 2y):}`

1) `((d^2)x)/(d(t^2)) = (4xdx)/(dt) + (6ydy)/(dt) `
`x'' = 4x' - 6y'`

2) `6y = 4x- x'`
` y = (4x-x')/6`
`y'= 4x + 2((4x-x')/6) = (32x - 2x')/6 `

3) `x'' = 4x' - 6((32x - 2x')/6) = 6x' - 32x`

`x'' - 6x' + 32x = 0`
`k^2-6k+32=0`
`D = -92`
`k_1` и `k_2` вот с ними тогда что?

@темы: Дифференциальные уравнения

---

[dunakov]

Закрытая запись, не предназначенная для публичного просмотра

---

Найти функцию распределения F(x).

[JrClap]

Имеется n заготовок для одной и той же детали. Вероятность изготовления годной детали из каждой заготовки равна p. Найти ряд распределения для случайного числа использованных заготовок. Найти функцию распределения F(x).

Тут надо использовать формулу Бернулли, но не знаю какие значения подставлять.

@темы: Теория вероятностей

---

Найти предел функции

[loz09]

Помогите найти предел `lim_{x->0} (x^5)/(tg(x)-2arcsin(x)+x)`
Подскажите, пожалуйста, с чего начать? Это вроде неопределенность вида 0/0 получается? Как ее решать дальше? Лучше сначала избавится от тангенса и свести все к синусам и косинусам или не надо этого делать? ПОМОГИТЕ

@темы: Пределы

---

Возможные значения

[wpoms.]

Пусть `x, y` - ненулевые действительные числа, которые удовлетворяют равенству `x^3 + y^3 + 3*x^2*y^2 = x^3*y^3`. Определите все значения, которые может принимать выражение `1/x + 1/y`.

@темы: Рациональные уравнения (неравенства)

---

[MisteryS]

1. Сколькими способами можно сделать флаг из трёх полос, если есть материал 5 разных цветов? Эта же задача, но если одна из полос должна быть красной?
2. Автомобильные номера состоят из одной, двух или трёх букв и четырёх цифр. Найти число таких номеров, если используются 32 буквы.
3. На полку нужно поставить 17 разных книг, из которых 10 синих и 7 красных. Сколькими способами это можно сделать так, чтоб все синии книги стояли рядом, если
а)порядок размещения всех книг имеет значение
б)учитывается только цвет книг
4. Сколькими способами из слова "логарифм" можно выбрать 2 согласные и 1 гласную букву? Таже задача, но среди выбранных должна быть буква "ф".
5.Сколькими способами можно выбрать одну согласную и одну гласную из слова "патрубок"? Рассмотреть два случая: порядок важен и не важен.
6. У одного человека есть 7 книг, у второго 9. Сколькими способами они могут обменять книгу одного на книгу второго?
7. Сколькими способами можно выбрать из колоды карт четыре карты так, тоб среди них были : а) карты всех мастей, б) карты разных названий, в) все катринки?
8. В комитет выбрано 9 человек. Сколькими способами из них можно выбрать главу, его заместителя, секретаря и казначея?
9. Сколькими способами можно выбрать 4 карты из полной колоды так, чтоб были три масти? Были 2 масти?
10. Сколько трёхзначных чисел можно составить из цифр 1, 2, 3, 4, 5? А если каждую цифру можно использовать не меньше одного раза?
11. Сколькими способами можно рассадить 9 человек в 3 вагона? А так, чтоб в каждом было по 3 еловека? А так, чтоб в один из вагонов не сел ни один человек.?
12. Сколько есть пятизначных чисел , которые одинаково итаются справа налево и слева направа?
13. Сколькими способами можно расставить 12 белых и 12 черных чашек на черных квадратах шахматной доски?

Сейчас буду скидывать своё решение...

@темы: Комбинаторика

---

[Tabry]

Извините за такой вопрос. Но просто очень нужно.
как посчитать?
`1/(7.24*10^-5)`

@темы: Школьный курс алгебры и матанализа

---

Прототипы B14 с W|A

[webmath]

Интерактивное решение "всех" прототипов B14 с Wolfram|Alpha
webmath.exponenta.ru/ege.html
webmath.exponenta.ru/edem/wa_b14_1.html
webmath.exponenta.ru/edem/wa_b14_2.html
webmath.exponenta.ru/edem/wa_b14_3.html
webmath.exponenta.ru/edem/wa_b14_4.html
Если беспонужно - скажете.

@темы: Полезные и интересные ресурсы, Производная, ЕГЭ

---

абсолютная погрешность разности и верные цифры

[tvims]

Здравствуйте. Прошу помочь разобраться с приближенными вычислениями.
Задача такая:
Найти разность `x – y` с тремя верными знаками, если `x = 12,1254 ± 0,0001`, `y = 12,128 ± 0,001`.
Решение.
`12,1254 – 12,128 = – 0,0026`
`Delta_u = 0,0001 + 0,001 = 0,0011`; `delta_u = 0,0011/|–0,0026| = 0,42`.
По-моему в числе -0,0026 вообще нет верных цифр. Но в методичке написано: "Согласно этим результатам разность `x – y` имеет не более одной верной цифры."
Вопрос:
Как записать этот результат с ТРЕМЯ верными знаками?

P.S. Не нашел среди предложенных темы "Вычислительная математика" или "Численные методы"

@темы: Приближенные методы вычисления корней уравнений

---

[Шиколада]

Прошу помощь в решении задачи.
Верно ли, что cos2000 меньше cos2001?

@темы: Тригонометрия

---

[Шиколада]

Помогите, пожалуйста, решить задачу. Дано уравнение касательной f(x)=2x+3. Требуется записать уравнение функции F(x), к которой эта касательная проведена.

@темы: Касательная

---

Теория множеств

[sorata]

Здравствуйте! Помогите, пожалуйста, понять, как решать, или оправдайте опасения об ошибке в задании =)

Задано множество U={1,2,3,4,5,6,7,8,9}.
Также даны множества:
A={1,3,5,7,9};
B={2,4,6,8};
C={3,6,9};
D={4,7,9};
E={2,5,8}.
Через них нужно выразить множество F={2,3}.
Элемент {3} я нашел так: `(A nn C) setminus D = {3}`
А выразить {2} никак не получается, так как во всех множествах, где этот элемент есть, он входит вместе с {8}.
Подскажите пожалуйста, что с этим можно сделать.

@темы: Дискретная математика

---

ТФКП

[Laila_Alex]

Здравствуйте.
Никак не могу понять, как вычислить (i)^(1/i).
Ничего похожего не нашла нигде(
Помогите пожалуйста.

@темы: ТФКП

---

"Особенные" числа

[wpoms.]

Для каждого натурального числа, имеющего каноническое разложение на множители `n = p_1^{a_1} * p_2^{a_2} * \ldots * p_k^{a_k}`, определим `t(n) = (p_1 + 1)*(p_2 + 1)*ldots*(p_k + 1)`. Например, `t(20) = t(2^2 * 5^1) = (2 + 1)(5 + 1) = 18`, `t(30) = t(2^1 * 3^1 * 5^1) = (2 + 1)(3 + 1)(5 + 1) = 72` и `t(125) = t(5^3) = (5 + 1) = 6`. Назовем натуральное число `n` особенным, если `t(n)` является делителем `n`. Сколько среди положительных делителей числа `546^10` особенных чисел?

@темы: Теория чисел