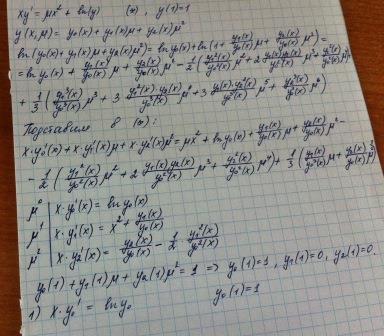Ракладываю в ряд `y=x, x in [0;2]`. Получаю, что коэффициент при косинусе обнуляется. Как такое может быть если исходная функция не обладает свойством четности?
понедельник, 04 апреля 2016
привет! помогите плиз решить задачу, надо до четверга. Десятичная запись натурального числа n содержит 61 цифру. Среди этих цифр есть тройки, четверки и пятерки. Других цифр нет. Число троек больше чем пятерок. Найти остаток от деления на 9.
Всe куда-то падают и куда-то попадают. (c)
Есть таблица. Нужно найти значение от отрицательного аргумента, например, от -0.5. Интуитивно понятно, что нужно из 100% вычесть значение для 0.5, но не совсем понятно почему?
суббота, 02 апреля 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Докажите, что для действительных чисел `a`, `b` (`a*b > 0`) выполняется неравенство `root(3){(a^2b^2(a + b)^2)/4} <= (a^2 + 10ab + b^2)/12`. Определите, при каких условиях достигается равенство. Докажите, как следствие или иным образом, что для всех действительных чисел `a`, `b` верно неравенство `root(3){(a^2b^2(a + b)^2)/4} <= (a^2 + ab + b^2)/3` Определите, при каких условиях достигается равенство. |  |
пятница, 01 апреля 2016
Эллипс - это круг, который можно вписать в квадрат 25х40
Уважаемые сообщники!
Поздравляю Вас с Днём Математика!
Желаю всем всяческих свершений в профессиональной сфере и просто по жизни!...
Поздравляю Вас с Днём Математика!
Желаю всем всяческих свершений в профессиональной сфере и просто по жизни!...
по традиции немного баянов...
четверг, 31 марта 2016
Step by step ...
ЕГЭ, 28 марта 2016 г.1
13. а) Решите уравнение `8^x -7*4^x - 2^(x+4) + 112 = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку `[log_2 5; log_2 11]`.
14. В правильной четырехугольной призме `ABCDA_1B_1C_1D_1` сторона основания `AB` равна 6, а боковое ребро `A A_1` равно `4sqrt3`. На ребрах `AB`, `A_1D_1` и `C_1D_1` отмечены точки `M `, `N` и `K` соответственно, причем `AM = A_1N = C_1K = 1`.
а) Пусть `L` – точка пересечения плоскости `MNK` с ребром `BC .` Докажите, что `MNKL` – квадрат .
б) Найдите площадь сечения призмы плоскостью `MNK`.
15. Решите неравенство: `(5x-13)*log_(2x-5) (x^2-6x+10) >= 0`.
16. Точка `O` – центр окружности, описанной около остроугольного треугольника `ABC`, `I` – центр вписанной в него окружности, `H` – точка пересечения высот. Известно, что `/_BAC = /_OBC + /_OCB`.
а) Докажите, что точка `I` лежит на окружности, описанной около треугольника `BOC`.
б) Найдите угол `OIH`, если `/_ABC = 55^@`.
17. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме того, в начале третьего и четвертого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 25 млн рублей.
18. Найдите все значения параметра `a`, при каждом из которых система уравнений
`(xy^2-3xy-3y+9)/sqrt(x+3) =0`,
`y = ax`
имеет ровно два различных решения .
19. Множество чисел назовем хорошим, если его можно разбить на два
подмножества с одинаковой суммой чисел.
а) Является ли множества {200;201;202;…;299} хорошим?
б) Является ли множество {2;4;8;…;2^100} хорошим?
в) Сколько хороших четырехэлементных подмножеств у множества {1;2;4;5;7;9;11}?
----------------------------------------------
1 alexlarin.net/ege/2016/280316.html
13. а) Решите уравнение `8^x -7*4^x - 2^(x+4) + 112 = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку `[log_2 5; log_2 11]`.
14. В правильной четырехугольной призме `ABCDA_1B_1C_1D_1` сторона основания `AB` равна 6, а боковое ребро `A A_1` равно `4sqrt3`. На ребрах `AB`, `A_1D_1` и `C_1D_1` отмечены точки `M `, `N` и `K` соответственно, причем `AM = A_1N = C_1K = 1`.
а) Пусть `L` – точка пересечения плоскости `MNK` с ребром `BC .` Докажите, что `MNKL` – квадрат .
б) Найдите площадь сечения призмы плоскостью `MNK`.
15. Решите неравенство: `(5x-13)*log_(2x-5) (x^2-6x+10) >= 0`.
16. Точка `O` – центр окружности, описанной около остроугольного треугольника `ABC`, `I` – центр вписанной в него окружности, `H` – точка пересечения высот. Известно, что `/_BAC = /_OBC + /_OCB`.
а) Докажите, что точка `I` лежит на окружности, описанной около треугольника `BOC`.
б) Найдите угол `OIH`, если `/_ABC = 55^@`.
17. Вклад планируется открыть на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а, кроме того, в начале третьего и четвертого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наибольший размер первоначального вклада, при котором через четыре года вклад будет меньше 25 млн рублей.
18. Найдите все значения параметра `a`, при каждом из которых система уравнений
`(xy^2-3xy-3y+9)/sqrt(x+3) =0`,
`y = ax`
имеет ровно два различных решения .
19. Множество чисел назовем хорошим, если его можно разбить на два
подмножества с одинаковой суммой чисел.
а) Является ли множества {200;201;202;…;299} хорошим?
б) Является ли множество {2;4;8;…;2^100} хорошим?
в) Сколько хороших четырехэлементных подмножеств у множества {1;2;4;5;7;9;11}?
----------------------------------------------
1 alexlarin.net/ege/2016/280316.html
1)На множестве N найти область значений и область определения бинарных отношений и указать, какими свойствами они обладают. p={(3;5);(5;3);(3;3)}
2)На множестве R найти область значений и область определения бинарных отношений и указать, какими свойствами они обладают. p=[0;2]x[1;4]
3)На множестве M={1,2,...,10} найти область значений и область определения бинарных отношений и указать, какими свойствами они обладают. xpx<=>(x*y=10)
2)На множестве R найти область значений и область определения бинарных отношений и указать, какими свойствами они обладают. p=[0;2]x[1;4]
3)На множестве M={1,2,...,10} найти область значений и область определения бинарных отношений и указать, какими свойствами они обладают. xpx<=>(x*y=10)
среда, 30 марта 2016
Здравствуйте. Помогите, пожалуйста, разобраться с двумя задачами.
в лотерею типа лото, если в лотерейный билет вносятся 12 чисел от 1 до 99 ("джек-пот" выигрывает билет, в котором оказались все двенадцать первых чисел, выданных машиной"
понедельник, 28 марта 2016
Не могли бы Вы проверить:
Дан круг радиусом `R`. Найти найти вписанный в него треугольник, площадь которого наибольшая.
Нужно составить задачу оптимизации и решить её.
Как мне уже посоветовали в предыдущем топике вполне логично составить задачу оптимизации:
`{(R^2/2(sin alpha + sin beta + sin (2pi-alpha-beta))->max ), (0<=alpha < pi), (0<=beta < pi):}`
Дальше можно было бы просто максимизировать сумму трех синусов, взяв производную по двум аргументам, получается:
`{(cos alpha - cos (alpha+beta) = 0),(cos beta -cos (alpha+beta) = 0):}`, вычитая поулчаем `cos alpha = cos beta`. Альфа и бета - углы от нуля до `2pi`, значит `alpha=beta` (или же `beta = 2pi-alpha`) и значит `cos alpha - cos (2alpha) = 0`, отсюда `[(alpha=0), (alpha=2pi/3), (alpha=4pi/3):}`. `alpha=0` очевидно неверно. Если `alpha=2pi/3`, то все центральные углы по 120, значит треугольник равносторонний (нужный ответ). Ну и, наконец, если `alpha = 4pi/3`, то `beta = alpha = 4pi/3`, что невозможно. Если же `beta = 2pi-alpha`, то `cos alpha = 1`, значит `alpha=0` (посторонний корень) или `alpha = pi`
Итого один ответ: все углы по 60 градусов.
Дан круг радиусом `R`. Найти найти вписанный в него треугольник, площадь которого наибольшая.
Нужно составить задачу оптимизации и решить её.
Как мне уже посоветовали в предыдущем топике вполне логично составить задачу оптимизации:
`{(R^2/2(sin alpha + sin beta + sin (2pi-alpha-beta))->max ), (0<=alpha < pi), (0<=beta < pi):}`
Дальше можно было бы просто максимизировать сумму трех синусов, взяв производную по двум аргументам, получается:
`{(cos alpha - cos (alpha+beta) = 0),(cos beta -cos (alpha+beta) = 0):}`, вычитая поулчаем `cos alpha = cos beta`. Альфа и бета - углы от нуля до `2pi`, значит `alpha=beta` (или же `beta = 2pi-alpha`) и значит `cos alpha - cos (2alpha) = 0`, отсюда `[(alpha=0), (alpha=2pi/3), (alpha=4pi/3):}`. `alpha=0` очевидно неверно. Если `alpha=2pi/3`, то все центральные углы по 120, значит треугольник равносторонний (нужный ответ). Ну и, наконец, если `alpha = 4pi/3`, то `beta = alpha = 4pi/3`, что невозможно. Если же `beta = 2pi-alpha`, то `cos alpha = 1`, значит `alpha=0` (посторонний корень) или `alpha = pi`
Итого один ответ: все углы по 60 градусов.
воскресенье, 27 марта 2016
Добрый вечер! Не могли бы Вы помочь с линейным программирвоанием?
Дана задача:
`{(x_1+2x_2+3x_3 -> max), (x_1+x_2<=2), (x_1+x_3<=3), (x_2>=x_3), (x_1<=1), (x_i>=0):}`
Нужно записать двойственную задачу и решить её. Предварительно нам дано решение исходной задачи: `(0,2,2)`
Прежде чем приступать к решению двойственной задачи я хотел спросить: а как вообще решать линейные задачи? Предположим, нам не было бы дано решение исходной системы, как её решать?
Дана задача:
`{(x_1+2x_2+3x_3 -> max), (x_1+x_2<=2), (x_1+x_3<=3), (x_2>=x_3), (x_1<=1), (x_i>=0):}`
Нужно записать двойственную задачу и решить её. Предварительно нам дано решение исходной задачи: `(0,2,2)`
Прежде чем приступать к решению двойственной задачи я хотел спросить: а как вообще решать линейные задачи? Предположим, нам не было бы дано решение исходной системы, как её решать?
Есть несколько точек в n-мерном пространстве, надо построить базис.
Берем среднюю точку, находим максимально удаленную точку и строим первый базисный вектор (u1 -вектор единичной длины, из точки X* в первую максимально удаленную точку ).
Затем строим второй, но вот с построением второго возникли проблемы. Нужно найти максимально удаленную точку от средней точки или от нового вектора?
Есть формула
в ней мы считаем скалярное произведение и умножаем на вектор((Xj-X*,u1)*u1),пусть будет Z , то есть изменяем длину вектора.
Расстояние находим || Xj - X*-Z||, считаем: из X* по координатно вычитаем Z (получим Y), а затем берем sqrt((Y1-Xj1)^2)+(Y2-Xj2)^2+...+(Yn-Xjn)^2).
Правильно ли я понял формулу? Или нужно: из Xj вычесть по координатно X*(получим A) и затем находить расстояние как sqrt((Z1-A1)^2)+...(Zn-An)^2).
Поясните пожалуйста как считать выражение || Xj - X*-Z||.
Скалярное произведение если =0, то векторы будут перпендикулярны, то есть то что нужно, но а если не равно нуля то как понимать это в n-мерном пространстве?
Берем среднюю точку, находим максимально удаленную точку и строим первый базисный вектор (u1 -вектор единичной длины, из точки X* в первую максимально удаленную точку ).
Затем строим второй, но вот с построением второго возникли проблемы. Нужно найти максимально удаленную точку от средней точки или от нового вектора?
Есть формула
в ней мы считаем скалярное произведение и умножаем на вектор((Xj-X*,u1)*u1),пусть будет Z , то есть изменяем длину вектора.
Расстояние находим || Xj - X*-Z||, считаем: из X* по координатно вычитаем Z (получим Y), а затем берем sqrt((Y1-Xj1)^2)+(Y2-Xj2)^2+...+(Yn-Xjn)^2).
Правильно ли я понял формулу? Или нужно: из Xj вычесть по координатно X*(получим A) и затем находить расстояние как sqrt((Z1-A1)^2)+...(Zn-An)^2).
Поясните пожалуйста как считать выражение || Xj - X*-Z||.
Скалярное произведение если =0, то векторы будут перпендикулярны, то есть то что нужно, но а если не равно нуля то как понимать это в n-мерном пространстве?
Найти 3 члена разложения решения по степеням малого параметра 𝝁 : 𝒙𝒚′=𝝁𝒙𝟐+𝒍𝒏𝒚,𝒚( 𝟏 ) =𝟏.
решила до первого дифф. уравнения. не могу его решить ((
Помогите, пожалуйста, решить..
решила до первого дифф. уравнения. не могу его решить ((
Помогите, пожалуйста, решить..
суббота, 26 марта 2016
Помогите пожалуйста разобраться с выводом, не понимаю с самого начала.
Пусть `f(x,y,z)` - некоторая функция, а `S` - замкнутая поверхность, ограничивающая объём `V` (рис. 26).
На отрезке `12`, параллельном оси `x`, `f` является функцией одного аргумента `x`. Интегрируя вдоль этого отрезка, получим `int_(12) (partial f)/(partial x)dx=f_2-f_1`,
где `f_1` и `f_2` - значения функции `f` на концах рассматриваемого отрезка.
Построим теперь бесконечно узкий цилиндр, одной из образующих которого является отрезок `12`. Пусть `dsigma` - площадь его поперечного сечения (величина существенно положительная). Умножим предыдущее соотношение на `dsigma`. Так как `dsigmadx` есть элементарный объём `dV`, заштрихованный на рисунке, то в результате получится
`int_(DeltaV) (partial f)/(partial x)dV=(f_2-f_1)dsigma`, где `Delta V` - часть объема `V`, вырезаемого из него поверхностью цилиндра.
Как понимаю `f(x,y,z)` - некоторая функция трёх переменных, областью определения которой являются некоторые точки пространства `RR^3`.
1) Не понимаю предложения На отрезке `12`, параллельной оси `x`, `f` является функцией одного аргумента `x` - это как представить? Как проекцию `f(x,y,z)` на ось `x`?
2) Если рассматривать функцию двух переменных `f(x,y)`, то тут даже не понятно, что будет её проекцией на ось, ведь она (функция) будет некоторой поверхностью в пространстве. Если геометрический смысл частной производной это тангенс угла `(partial z)/(partial x)=tg(alpha)`, то тогда подынтегральное выражение вроде как будет `dz=(partial z)/(partial x)dx`, то есть приращение `dz`, а не `dx`. Как получают кусок `dx`?
3) Как понимать интеграл по отрезку? Как определенный интеграл от `x_1` до `x_2`? А по объёмной области?
Пусть `f(x,y,z)` - некоторая функция, а `S` - замкнутая поверхность, ограничивающая объём `V` (рис. 26).
На отрезке `12`, параллельном оси `x`, `f` является функцией одного аргумента `x`. Интегрируя вдоль этого отрезка, получим `int_(12) (partial f)/(partial x)dx=f_2-f_1`,
где `f_1` и `f_2` - значения функции `f` на концах рассматриваемого отрезка.
Построим теперь бесконечно узкий цилиндр, одной из образующих которого является отрезок `12`. Пусть `dsigma` - площадь его поперечного сечения (величина существенно положительная). Умножим предыдущее соотношение на `dsigma`. Так как `dsigmadx` есть элементарный объём `dV`, заштрихованный на рисунке, то в результате получится
`int_(DeltaV) (partial f)/(partial x)dV=(f_2-f_1)dsigma`, где `Delta V` - часть объема `V`, вырезаемого из него поверхностью цилиндра.
Как понимаю `f(x,y,z)` - некоторая функция трёх переменных, областью определения которой являются некоторые точки пространства `RR^3`.
1) Не понимаю предложения На отрезке `12`, параллельной оси `x`, `f` является функцией одного аргумента `x` - это как представить? Как проекцию `f(x,y,z)` на ось `x`?
2) Если рассматривать функцию двух переменных `f(x,y)`, то тут даже не понятно, что будет её проекцией на ось, ведь она (функция) будет некоторой поверхностью в пространстве. Если геометрический смысл частной производной это тангенс угла `(partial z)/(partial x)=tg(alpha)`, то тогда подынтегральное выражение вроде как будет `dz=(partial z)/(partial x)dx`, то есть приращение `dz`, а не `dx`. Как получают кусок `dx`?
3) Как понимать интеграл по отрезку? Как определенный интеграл от `x_1` до `x_2`? А по объёмной области?
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Докажите, что (a) `(2*n)/(3*n + 1) <= sum_{k = n + 1}^{2*n} 1/k`, (b) `sum_{k = n + 1}^{2*n} 1/k <= (3*n + 1)/(4*(n + 1))`, для всех натуральных чисел `n`. | |
четверг, 24 марта 2016
Дана правильная пирамида SABC, у которой сторона основания АВ=6, а боковое ребро SА=9. Сечение пирамиды, параллельное ребрам AC и SB , является квадратом. Найдите угол между диагональю этого квадрата и плоскостью основания пирамиды
Что дальше делать? Или у меня ошибка в рассуждениях?
Что дальше делать? Или у меня ошибка в рассуждениях?
понедельник, 21 марта 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Докажите, что если нечетное простое число `p` можно представить в виде `x^5 - y^5`, где `x`, `y` целые числа, то `sqrt((4*p + 1)/5) = (v^2 + 1)/2`, для некоторого нечетного числа `v`. | |
Здравствуйте, столкнулся с проблемой понятия материала:
Находим вектор u1
u1=(x^(S1) -x*)|| x^( S1)- x*||^(-1)
что означают эти скобки и как найти этот вектор если x^(S1) -это точка и x* это тоже точка.
Что означают ||...||, если это норма то что и как делать?
Находим вектор u1
u1=(x^(S1) -x*)|| x^( S1)- x*||^(-1)
что означают эти скобки и как найти этот вектор если x^(S1) -это точка и x* это тоже точка.
Что означают ||...||, если это норма то что и как делать?
воскресенье, 20 марта 2016
Простыми словами
His wife would bemoan the fact that weekends had to be spent on research, because Bill feared that mathematical inspiration would dry up before he was 40 (at least, that's what he told her). Его жена сокрушалась, что все выходные он посвящал исследованиям, потому что Билл боялся, что математическое вдохновение иссякнет к сорока годам (по крайней мере, так он ей говорил) Норман Биггс об Уильяме Татте |
Это топик не приурочен ко дню рождения. Он инспирирован интересом VEk к научной деятельности и биографии Уильяма Татта.
Это замечательное фото сделано Полом Халмошем.
Википедия
Уильям Томас Тат (англ. William Thomas Tutte; 14 мая 1917 — 2 мая 2002) — британский, позднее канадский криптограф и математик. Во время Второй Мировой Войны внес значительный вклад в расшифровку шифра Лоренца, главной немецкой шифровальной системы, использовавшейся для секретных коммуникаций главнокомандующими Вермахта. Кроме того, известен своими достижениями в математике.
Начало жизни и образование
Уильям Тат родился 14 мая 1917 года в городе Ньюмаркет в Саффолке, в семье садовника. Получил степень бакалавра по специальности химия в Тринити-колледж (Кембридж). В аспирантуре продолжил изучать физическую химию, но перевелся на математику в конце 1940. В 1941 получил степень Магистра Наук.
Вторая Мировая Война
Вскоре после начала Второй Мировой Войны учитель Тата, Партик Дафф, посоветовал его для работы в Центре правительственной связи в Блетчли Парк. После интервью Уильям был послан на учебные курсы в Лондон, а после присоединился к научно-исследовательской части в Блетчли Парке. Сначала он работал над шифровальной машиной Хагелина, использовавшейся Итальянским военно-морским флотом. Это была роторная шифровальная машина, доступная в промышленных масштабах, так что механизмы кодирования были известны, и дешифрование сообщений требовало только определения настроек машины.
Анализ шифра Лоренца
31 августа 1941 года германским оператором было послано сообщение в 4500 знаков. Сообщение было получено с ошибками, после чего было передано повторно с небольшими изменениями, но тем же самым ключом. Это позволило Джону Тильтману, ветерану Блетчли-парка, сделать вывод о том, что это был шифр Вернама, и получить текст двух сообщений и ключ. После безрезультатных попыток криптоаналитиков взломать код машины Танни, имеющаяся информация была передана Тату для дальнейшей работы. Тат начал расшифровку с использования метода Касиски, заключающегося в поиске групп символов, которые повторяются в зашифрованном тексте. С помощью него он установил, что длина ключевого слова равна сорока одному символу. Эту компоненту ключа Тат назвал `chi_1` (хи1). Однако, было ясно, что устройство ключа сложнее, то есть существовала и другая компонента, которую он назвал `psi_1` (пси1). Таким образом, машина состояла из `psi` и `chi` дисков, генерирующих каждые пять бит символа. Тат выяснил, что `psi` и `chi` компоненты ключа объединялись функцией XOR. То есть для каждого символа ключ K можно было представить следующим образом:
`K = chi oplus psi`
После того, как Тат сделал вывод о `psi`-компоненте, другие исследователи присоединились к изучению структуры машины. В течение следующих двух месяцев Татт и другие члены исследовательской группы Блетчли-парка восстанавливали логическую структуры шифровальной машины.
читать дальше
От себя хочу сказать вот что. Русскоязычная статья в Википедии появилась не так давно. Когда этот топик только задумывался, ее еще не было. И поскольку мне приходилось читать всякие источники, я вижу, насколько она сухая и мало информативная. Поэтому попытаюсь восполнить эту сухость разными сведениями и ссылками.
Вот, например, та самая машина Лоренца, которую дешифровали в Блетчли-парке.
Фото из английской Википедии.
The Lorenz SZ machines had 12 wheels each with a different number of cams (or "pins").
Фото из немецкой Википедии
Lorenz SZ42
Ссылки.
1. Прекрасная статья Забытый творец технологий: Билл Татт или Алан Тьюринг?
Вот цитата из нее:
Последний оставшийся в живых шифровальщик, капитан Джерри Робертс, который умер в марте 2014 года, описал в своем интервью 2009 г. о том, что Татту потребовалось два с половиной месяца настойчивой напряженной работы, чтобы выяснить структуру машины Лоренца.
“Татт был замкнутым, круглолицым человек, который работал со мной в одной комнате,’’ — сказал он. — “и когда он сидел, положив карандаш и уставившись вдаль, я думал, что он не отрабатывает свой хлеб, но я был неправ. Тьюринг, по крайней мере, видел и рассматривал Энигму до войны, но Татт ни разу до окончания войны не видел машину Лоренца. Это было блестящее достижение, названное одним из комментаторов “выдающимся интеллектуальным подвигом прошлого века’’’’.
2. Вот математическая статья Матрица Татта
3. Вот на сайте МЦМНО среди прочих математический сюжет: Ю.М. Бурман. Многочлен Татта и модель случайных кластеров
Англоязычные ссылки:
1. Forgotten tech father: Bill Tutte vs. Alan Turing? (Это источник первой русскоязычной ссылки.
2. Просто несколько фото ) Билл Татт
3. Codebreakers: Bletchley Park’s Lost Heroes
4. Bill Tutte: The unsung codebreaking hero of World War Two ВВС news. Очень интересная статья! Даже если просто полистать и посмотреть на картинки — рекомендую!
5. Professor Bill Tutte The Telegraph
Помогите, пожалуйста, с решением следующей задачи: Дан квадрат со стороной 10. Разрежьте его на 100 равных четырехугольника, каждый из которых вписан в окружность радиуса корень из 3. Задача с турнира городов. Думаю конкурс уже прошел во всех городах.
суббота, 19 марта 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Дан треугольник `ABC`. Длины сторон `BC`, `CA`, `AB` равны `a`, `b`, `c`, соответственно. Точки `D`, `E` являются серединами сторон `AC`, `AB`, соответственно. Докажите, что `BD` перпендикулярен `CE` тогда и только тогда, когда `b^2 + c^2 = 5*a^2`. | |