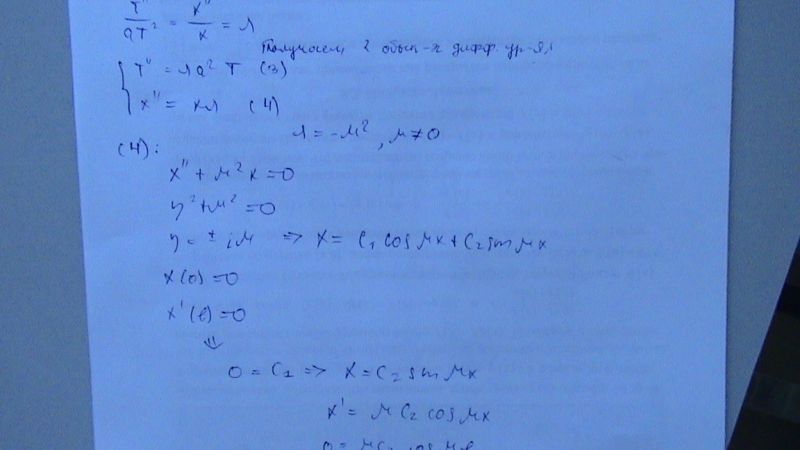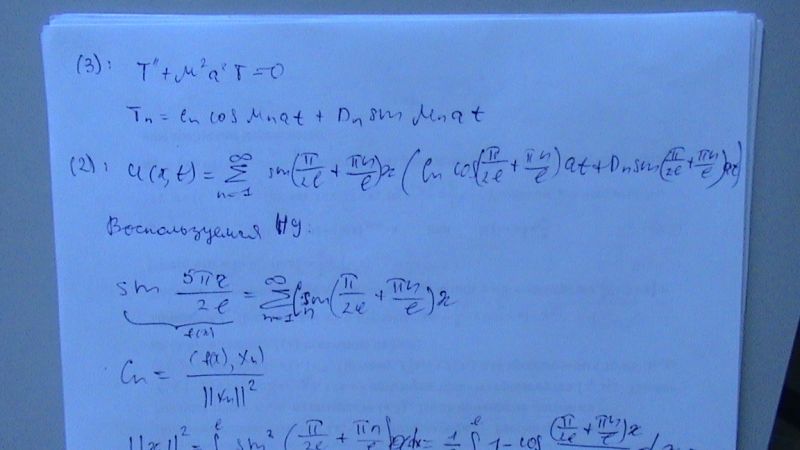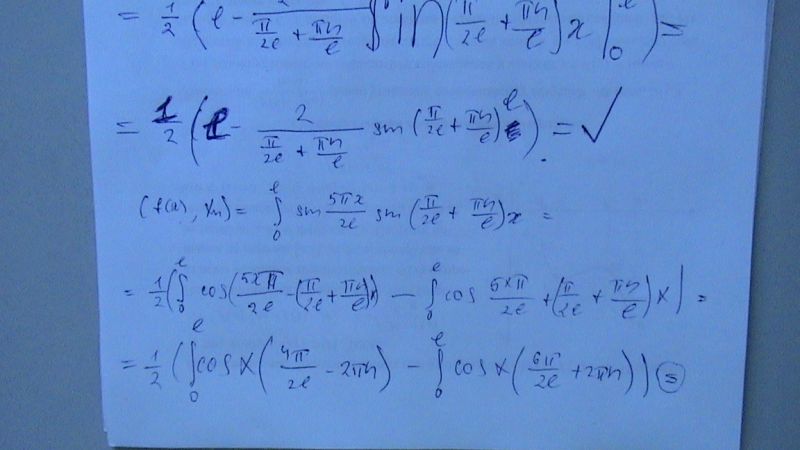Интеграл от дроби

[Marina Petrelli]

Здравствуйте. Задание таково. `int (3x-2)/(x^3-1) dx`Этот интеграл = I.Я нашла, что `A=1/3`, `B=-(1/3)`, `C=7/3`
Далее, `I=int((1/3)/(x-1)+(-(1/3)x+(7/3))/(x^2+x+1))dx = 1/3ln(x-1)-1/3int ((xdx)/(x^2+x+1)+7/3int(dx/(x^2+x+1)` Я думаю, что я неправильно раскладываю `int(-(1/3)x+(7/3))/(x^2+x+1)dx` Помогите пожалуйста! Заранее благодарна.

@темы: Интегралы

---

помогите пожалуйста найти объем

[sasha-s]

(x^2+y^2+z^2)^2=a^3*x

@темы: Математический анализ

---

Тригонометрия 2 уравнения

[Cat_CooLeR]

Здравствуйте! Пожалуйста натолкните на мысль, как решать данные уравнения:
1. `(12*sin(x)-5*cos(x))*(13*cos(2*x)-20*cos(x)-11)=362`
Здесь у меня полный завал, т.к. приведение левой скобки к одной функции с помощью введения дополнительного аргумента и разложения в правой никак не помогло.
2. `ctg(x)+ctg(3*x)-tg(2*x)=0`
В этом уравнении я делал так: представил tg2x=1/ctg2x, раскрыл по формулам ctg3x и ctg2x, и сделать замену t=ctgx, но получилось уравнение шестой степени... так же была идея представить ctgx и tgx через sin и cos, но так же результата не дало.
Буду благодарен за подсказку!

@темы: Тригонометрия

---

Теория сравнений.

[Леди Катрина]

Помогите, пожалуйста, найти литературу по теории сравнений на вопрос "Обращение обыкновенной дроби в десятичную дробь и определение длины периода систематической дроби".

@темы: Литература

---

[wpoms.]

Математическая олимпиада в Ирландии Первый раунд олимпиады проводился в этом учебном году во второй раз. Количество заданий, по сравнению с прошлым учебным годом, уменьшено с 10 до 6. `26^{th}` Irish Mathematical Olympiad / 12-16 November 2012, Round 1 `26^{th}` Irish Mathematical Olympiad / 12-16 November 2012, Round 1 1. Площадь вписанного в окружность квадрата равна `8`. Найдите площадь круга. 2. На планете Галл неделя состоит из `8` дней, в каждом месяце `34` дня и год состоит из `14` месяцев. Если первый день года приходится на Понедельник, то жители планеты празднуют день Закрытых Банков. Если сегодня на Галл отмечают день Закрытых Банков, то через сколько дней состоится следующий день Закрытых Банков? 3. В бальном зале танцует некоторое количество пар, состоящих из одного мужчины и одной женщины. Всего танцуют `2//3` от общего количества мужчин и `3//4` от общего количества женщин. Какая часть людей в бальном зале танцует? 4. В треугольнике `ABC` прямой угол `B`, `AB = 2` и `BC + AC = 4`. Найдите длину `BC`. 5. `12` ноября `2012` года Марии исполнилось `7` лет. Она заметила, что ее возраст равен сумме цифр года, в котором она родилась. Когда Мария рассказала об этом своей тете Уне, то тетя ответила, что то же самое случилось с ней в ее день рождения ранее в этом году. Сколько лет было Уне, когда родилась Мария? 6. Числа `0,1,2,3,4,5,6,7,8` напечатаны на девяти карточках, по одному числу на каждой карточке. Некоторые карточки зеленого цвета, а остальные - оранжевые. Число `1` напечатано на зеленой карточке. Известно, что если числа `a` и `b` на зеленых карточках, то числа `a - b` и `a + b` напечатаны на карточках другого цвета. Сколько всего зеленых карточек? No calculators allowed / Time allowed: 30 minutes

@темы: Олимпиадные задачи

---

Взаимное расположение двух плоскостей

[Marylinek]

Как найти взаимное расположение 2-ух плоскостей, если даны их уравнения?

@темы: Аналитическая геометрия

---

Группировка статистических данных

[Сильвана Ветрокрылая~]

А как насчет статистики?

Здравствуйте. Задали задачку.
Провести группировку исследуемой совокупности

условия

Номер предпри­ятия - Стоимость ос­новных фондов, млн руб
1 - 119,0
2 - 28,1
3 - 15,9
4 - 36,8
5 - 17,5
6 - 50,3
7 - 55,9
8- 26,1
9 - 21,6
10 - 25,4
11 - 17,2
12 - 119,6
13 - 124,2
14 - 114,8
15 - 166,5
16 - 103,5
17 - 141,1
18 - 154,2
19 - 24,4
20 - 196,5

Собственно, подобные задачки мной решались, и вызывает проблему лишь одно: когда строю график Огивы, он получается не плавный (как обычно решали), а скачкообразный. А в этом случае остальное решение идет не по формуле, а по графику.
Так ли это, если так, подскажите, как в итоге решить это?
p.s. у меня по графику выходит всего 2 интервала.

@темы: Математика в экономике, Математическая статистика

---

[Marylinek]

Как найти расстояние от точки до прямой заданной в пространстве своим каноническим уравнением? Например от точки Р(-1,1,2) до прямой L: x-1/-1=y-2/2=z-3/4

@темы: Аналитическая геометрия, Прямая и плоскость в пространстве

---

[polinapolin]

Добрый вечер! Помогите, пожалуйста.
Задание из Проскурякова. (1449)
Показать, что умножение квадратных матриц второго порядка а) слева б) справа
на матрицу `((a,b),(c,d))` является линейным преобразованием пространства всех матриц второго порядка, и найти матрицы этих преобразований в стандартном базисе матриц.

1) а) Пусть `A,B\ \in\ \X`, `C=((a,b),(c,d))`
`varphi*(A+B)=C*(A+B)=C*A+C*B=varphi*A+varphi*B`
`varphi*(alpha*A)=C*(alpha*A)=alpha*C*A=alpha*varphi*A`
Вроде так можно доказать, верно? (Пункт б) аналогичен)

2) А вот, что делать с нахождением матрицы преобразований не понимаю. Почему матрица С не является матрицей оператора? Вроде как каждой квадратной матрице второго порядка ставится в соответствие при помощи умножении на матрицу С другая матрица.
Заранее спасибо!

@темы: Линейная алгебра, Матрицы

---

Помогите, пожалуйста, решить неопределённые интегралы!

[konaa]

интеграл( (ln(x)dx)/x^4)
интеграл( (2*x+5)/(x^3-4*x) )dx
интеграл( (7*x+8)/(4*x+6)^(1/3) )dx

@темы: Интегралы

---

Рекуррентные события, производящие функции

[~Шелли~]

Помогите, пожалуйста, разобраться... Есть задача:
Пусть `varepsilon` - возвратное непериодическое рекуррентное событие. Допустим, что время возвращений имеет конечное среднее `mu` и дисперсию `sigma^2`. Положим `q_n=f_(n+1)+f_(n+2)+...` и `r_n=q_(n+1)+q_(n+2)+...`. Показать, что производящие фукнкции `Q(s)` и `R(s)` сходятся при `s=1`. Доказать, что
`u_0+sum_(n=1)^inf (u_n-1/mu)*s^n = (R(s))/(mu*Q(s))`
и что поэтому
`u_0+sum_(n=1)^inf (u_n-1/mu) =(sigma^2-mu+mu^2)/(2*mu^2)`

Сходимость доказать получилось, а вот что делать с первым и вторым равенством, не понимаю, из-за этого застряла вся курсовая. Кто-нибудь может натолкнуть на мысль, как здесь действовать?

@темы: Теория вероятностей

---

Найти площадь фигуры ограниченной графиками функций

[Godness17]

Прошу помощи в решении.
Если правильно понимаю нужно брать два интеграла? один по y с 0 до 4, второй тоже по y с 1 до 4.
xy=-1, x=-y^(1/2), y=4
http://static.diary.ru/userdir/2/4/1/0/2410078/78235413.jpg
Что делаю:
1) Сначала беру интеграл с 0 по 4 integral -y^(1/2)dy=-16/3
2) Далее с 1 до 3 integral -1/y*dy=-1.4
Но как видите значение далеко от истины

@темы: Приложения определенного интеграла, Аналитическая геометрия

---

Мат. физика

[Afu-Ra]

Здравствуйте, проверьте пожалуйста задачку. Она на первый взгляд кажется большой, а проверить недолго можно, я думаю.

Найти колебания струны, если один конец `x=0` закреплен жестко, а второй `x=l` свободен. Начальное отклонение `u(x,0)=sin(5*pi*x)/(2l)` , начальные скорости `u_t=sin(pi*x)/(2l)`

Решение

Я не стал пока что искать коэффицент `D_n` . Надо сначала разобраться правильно ли я решаю . Подскажите.

@темы: Уравнения мат. физики

---

УМФ Гармоническая ли функция?

[...Полярная Звезда...]

(dx/dx_1)^2 - (du/dx_2)^2
Дана такая функция. Является ли она гармоничной? d не интеграл и как производная.
Вот что у меня получилось, в ответе написано да.
Я вот пришла к такому ответу,что с чем сократить? Или я неправильно производные нашла?

@темы: Уравнения мат. физики

---

Теория Вероятностей

[nastik009]

вероятность изготовления консервной банки с недостаточной герметизацией равна 0,02, Среди скольких банок, отобранных случайным образом, можно с вероятностью 0,9 , ожидать отсутствие бракованных.

Есть решение по формуле Бернулли

конкретно здесь непонятно, почему m=0, также ответ не совпадает с ответом в задачнике (n=50), какую еще формулу применить не знаю, помогите пожалуйста.

@темы: Теория вероятностей, Математическая статистика

---

Теория графов на английском.

[choucroute]

Прошу помощи у специалистов в области теории графов , знающих английский язык, подскажите, пожалуйста, где в этой задаче сказано , чему равна стоимость дугового потока?

@темы: Теория графов

---

Планиметрия

[wpoms.]

Дана окружность `S` и ее хорда `AB`, `M` - середина дуги `AB`. Пусть `P` - точка отрезка `AB` отличная от его середины. Продолжение отрезка `MP` пересекает `S` в точке `Q`. Пусть `S_1` - окружность, которая касается отрезков `AP` и `MP`, а также окружности `S`, и пусть `S_2` - окружность, которая касается отрезков `BP` и `MP`, а также окружности `S`. Общие внешние касательные к окружностям `S_1` и `S_2` пересекаются в точке `C`. Докажите, что `/_MQC = 90^o`.

@темы: Планиметрия

---

[bibliotekar.3]

Пара книг с alleng.ru

• Балаян Э.Н. Геометрия. 7-9 классы. Задачи на готовых чертежах для подготовки к ГИА и ЕГЭ 5-е изд., испр. и доп. - Р. на/Д.: 2013. - 223 с.
  
• Балаян Э.Н. Геометрия. 10-11 классы. Задачи на готовых чертежах для подготовки к ЕГЭ - Р. на/Д.: 2013. - 217 с.

Аннотации и ссылки для ознакомления

P.S. Ранее в топике Литература по геометрии для школьников выкладывалась книга Э. Н. Балаян Геометрия. Задачи на готовых чертежах. 7-9 классы - Феникс, 2009, 192 с.

@темы: Литература

---

Пожалуйста, посмотрите.

[Miriada11]

Посмотрите, пожалуйста, правильно ли я начала решения?

1. Найти массу окружности x^2+y^2=R^2, если линейная плотность в каждой точке равна |y|.

`m=int_a^b p*sqrt(1+(y')^2dx`, p- плотность.

`|y|=sqrt(R^2-x^2)`

m=`int_0^(2Pi) sqrt(R^2-x^2) *sqrt(1-R^2-x^2)dx`.......

2. Найти массу неоднородной фигуры (Ф), ограниченной линиями или поверхностями.

Фигура- `x^2+y^2=4`, `z=0`, `z=4-x-y`

Плотность `p= sqrt( x^2+y^2)`



`m=iiint_V dxdydz=iint_(VOxy) dxdy int`.......( не могу понять, как расставлять пределы внутренние. Вообще, сам принцип не могу понять. Сначала двигаемся вдоль оси Oz снизу вверх?Записываем функции, которые ограничивают фигуру снизу и сверху соответствено?) ` sqrt( x^2+y^2)=` затем перехожу в цилиндрическую систему координат=`iint_(VOxy) dxdy int`p dp dф`=....

3. Вычислить двойным или тройным интегрированием объём тела, ограниченного данными поверхностями:
`z=x^2+y^2`, `z=2x^2+2y^2`, `x^2+y^2=2x`.

Получается, что ` z=x^2+y^2, z=2x^2+2y^2`- параболоиды, `а x^2+y^2=2x`- цилиндр.

Для цилиндра:` (x-1)^2+y^2=1`

@темы: Кратные и криволинейные интегралы, Интегралы

---

Здравствуйте, подскажите решение задачи.

[АлександрКВ]

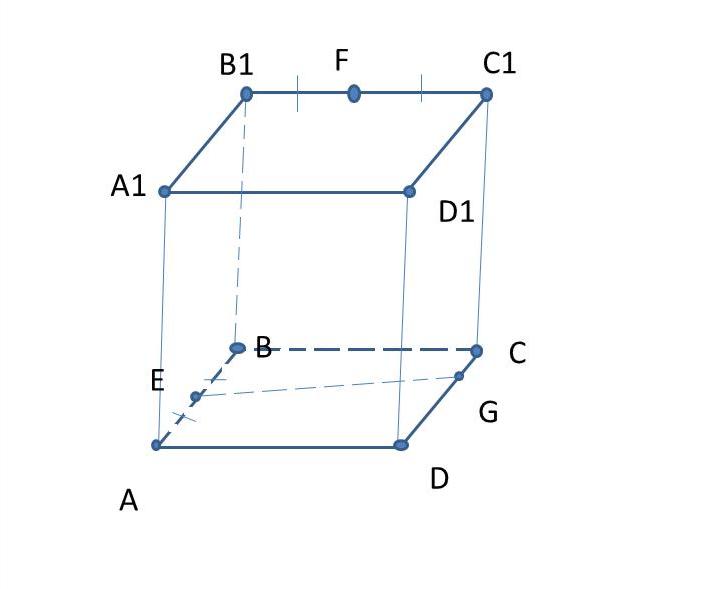
В основании прямой призмы ABCDA1B1C1D1 лежит ромб ABCD со стороной корень из 21 и углом A, равным 60 градусов. На рёбрах AB, B1C1 и DC взяты соответственно точки E, F и G так, что AE=EB, B1F=FC1 и DG=3GC. Найдите косинус угла между плоскостями EFG и ABC, если высота призмы равна 4,5 .

Одна проблема : не могу правильно построить соответствующий линейный угол.
Рисунок

@темы: ЕГЭ