Здравствуйте, проверьте пожалуйста задачку. Она на первый взгляд кажется большой, а проверить недолго можно, я думаю.
Найти колебания струны, если один конец `x=0` закреплен жестко, а второй `x=l` свободен. Начальное отклонение `u(x,0)=sin(5*pi*x)/(2l)` , начальные скорости `u_t=sin(pi*x)/(2l)`
Решение
Я не стал пока что искать коэффицент `D_n` . Надо сначала разобраться правильно ли я решаю . Подскажите.
Найти колебания струны, если один конец `x=0` закреплен жестко, а второй `x=l` свободен. Начальное отклонение `u(x,0)=sin(5*pi*x)/(2l)` , начальные скорости `u_t=sin(pi*x)/(2l)`
Решение
Я не стал пока что искать коэффицент `D_n` . Надо сначала разобраться правильно ли я решаю . Подскажите.

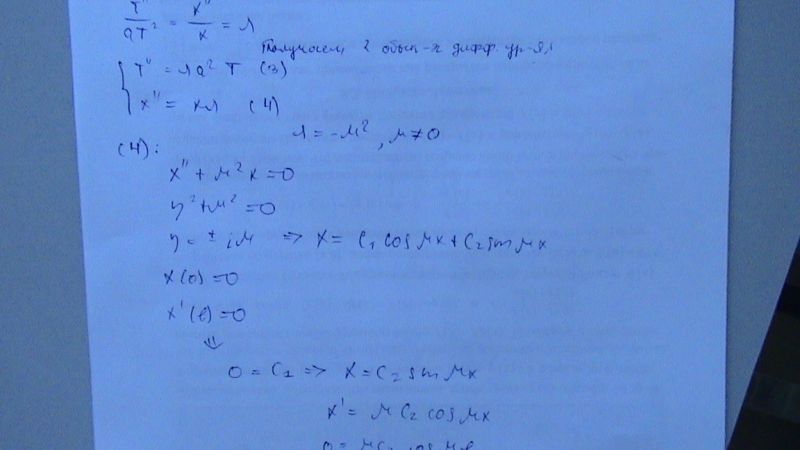

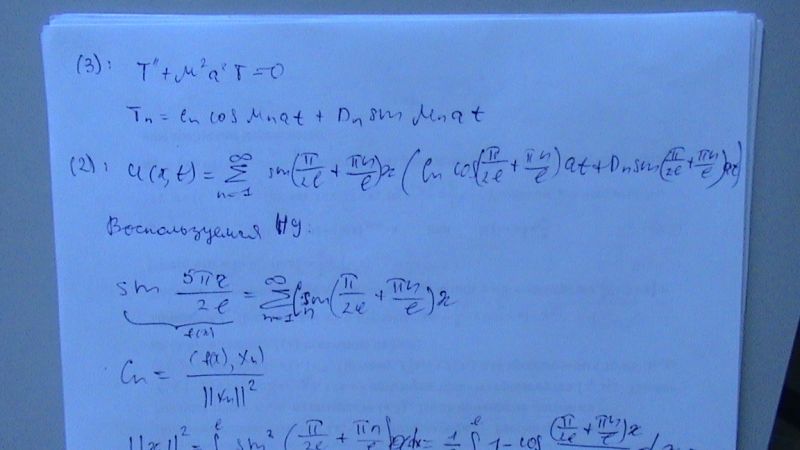

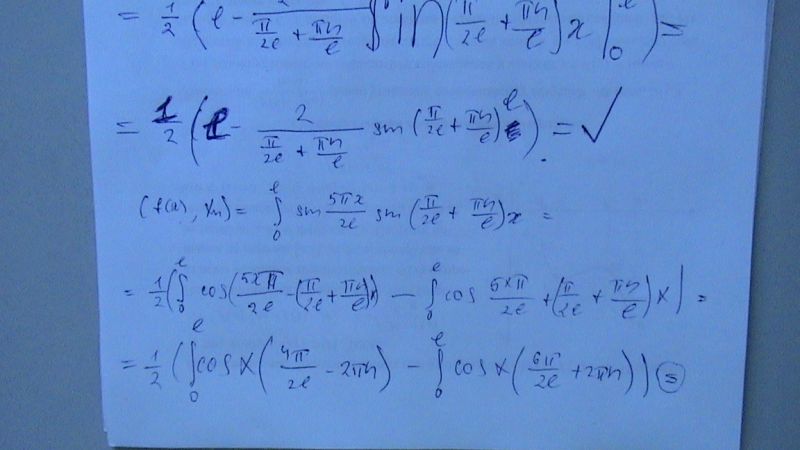


-
-
21.04.2013 в 18:12Просто для гиперболического уравнения более традиционный подход - формула Даламбера и метод продолжения...
-
-
21.04.2013 в 22:06-
-
21.04.2013 в 22:31Смысл верный... но беглый осмотр решения привёл к такому вопросу...
Вроде, `sin({5*pi*x}/{l})` является найденной собственной функцией при `n = 2`... Разве из единственности решения не должно вытекать, что все коэффициенты `C_n = 0`, кроме `C_2 = 1`?...
И ещё, вроде, `n` должно быть от нуля...
-
-
21.04.2013 в 23:23Тогда так получается
Да?
Почему `n` от нуля?
-
-
21.04.2013 в 23:33Ну, коэффициенты такие... но тогда ответ уже не будет бесконечной суммой... там только два слагаемых останутся...
-
-
21.04.2013 в 23:55Так да?
-
-
21.04.2013 в 23:58-
-
22.04.2013 в 00:13`u(x,t)=sin((pi*x)/(2l))*(2l)/(pia)*sin((pi*a*t)/(2l))+sin((5pi*x)/(2l))*cos((5pi*a*t)/(2l))`
-
-
22.04.2013 в 00:17-
-
22.04.2013 в 00:18-
-
23.04.2013 в 18:42-
-
23.04.2013 в 19:27