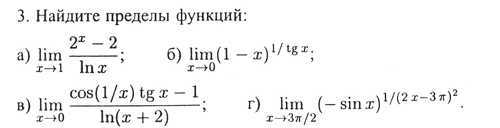понедельник, 14 марта 2011
1. В наклонной треугольной призме расстояния между боковыми ребрами равны 5 см, 12 см 13 см. Площадь меньшей боковой грани равна 22 см2. Найдите объем призмы.
2. Две боковые грани наклонной треугольной призмы образуют угол 60°; расстояние от их общего ребра до двух других ребер равно 5 см; боковое ребро призмы равно 8 см. Найдите боковую поверхность призмы.
3. Две боковые грани наклонной треугольной призмы перпендикулярны. Сумма их площадей равна 70 см2. Длина бокового ребра равна 5 см. Объем призмы равен 120 см3. Найдите расстояния между боковыми ребрами призмы.
Заранее спасибо.
2. Две боковые грани наклонной треугольной призмы образуют угол 60°; расстояние от их общего ребра до двух других ребер равно 5 см; боковое ребро призмы равно 8 см. Найдите боковую поверхность призмы.
3. Две боковые грани наклонной треугольной призмы перпендикулярны. Сумма их площадей равна 70 см2. Длина бокового ребра равна 5 см. Объем призмы равен 120 см3. Найдите расстояния между боковыми ребрами призмы.
Заранее спасибо.
Подскажите пожалуйста исчерпывающую литературу(книги,задачники,методички) по различным методам интегрирования с примерами.Изучил Фихтенгольца(курс диффер.и интегр. исчисления-2 том),но там не все рассмотрено,что нужно...
Заранее спасибо.
Заранее спасибо.
Что нужно сделать для того чтобы доказать что множество матриц M является подпространством в пространстве всех матриц данного размера?
Какие действия?
M-множество матриц (симметричные матрицы)
Какие действия?
M-множество матриц (симметричные матрицы)
С трудом,но доходит.
Доброе время суток!
Задание: В цилиндре проведено сечение под углом 60 градусов так,что оно полностью проектируется на основание цилиндра имеющего радиус равный 10 см.Определите площадь сечения.
Мне главное с чертежом определиться...
читать дальше
Задание: В цилиндре проведено сечение под углом 60 градусов так,что оно полностью проектируется на основание цилиндра имеющего радиус равный 10 см.Определите площадь сечения.
Мне главное с чертежом определиться...
читать дальше
Составить уравнение касательной к кривой `y = ln x` в точке, где она перпендикулярна к прямой `2x + 3y = 1`
Какой здесь правильный ход решения?
Уравнение касательной если не изменяет память : `y = f(a) + f '(a) (x - a)`
Какие у меня есть предположения... для начала можно выразить уравнение прямой, к которой касательная должна быть перпендикулярна:
` y = 1/3 - 2/3x `
Производная функции ` 1 / x` и тут вроде бы надо подставить `a` как `-1/k` где к коэффициент при Х в той прямой.
Если так то получается ` 1 / (2/3) = 3/2` `f '(3/2) = 2/3 ` в итоге получим уравнение касательной вида:
`y = ln(3/2) + 2/3x - 1`
но наверное всё не правильно)
Какой здесь правильный ход решения?
Уравнение касательной если не изменяет память : `y = f(a) + f '(a) (x - a)`
Какие у меня есть предположения... для начала можно выразить уравнение прямой, к которой касательная должна быть перпендикулярна:
` y = 1/3 - 2/3x `
Производная функции ` 1 / x` и тут вроде бы надо подставить `a` как `-1/k` где к коэффициент при Х в той прямой.
Если так то получается ` 1 / (2/3) = 3/2` `f '(3/2) = 2/3 ` в итоге получим уравнение касательной вида:
`y = ln(3/2) + 2/3x - 1`
но наверное всё не правильно)
точка s равноудалена от каждой из сторон правильного треугольника ABC на `sqrt(39)` см. Найдите угол между прямой SA и плоскостью `(ABC)`, если `AB=6` см
С трудом,но доходит.
Доброе время суток!
Я решить решила,а чем доказать не знаю...
Условие:
В окружности проведены пересекающиеся хорды `AK` и `BC`. Угол BAK=47 градусов.,а угол `BKC`=112 градусов.Определить угол `CBK`
Какое свойство применить?
Я решить решила,а чем доказать не знаю...
Условие:
В окружности проведены пересекающиеся хорды `AK` и `BC`. Угол BAK=47 градусов.,а угол `BKC`=112 градусов.Определить угол `CBK`
Какое свойство применить?
Всей душой хочу теперь я вперёд стремиться, счастье строить своею рукой. Пускай идти по этой дороге сложно, но знаю я: солнце всегда светит мне так ярко. Я не сдамся ни за что и никогда!
В правильной шестиугольной призме `A...F_1`, все ребра которой равны 1 найдите синус угла между:
1) прямой `BD_1` и плоскостью `BCE_1`
2) прямой `B_1E` и плоскостью `BCE_1`
Решение:
Первая задача:
1) Находим точку пересечения `N` прямой `BD_1` и `(E_1C_1C)`. Линия пересечения находится из прямоугольного треугольника `DBD_1`
2) Из точки `N` опускаем пер-ляр `NO` на `(BCE_1)` (`NO=sqrt(3)/4`)
3) `sin<NBO=sqrt(3)/8`
Вторая задача:
1) Треугольник `BB_1F_1` прямоугольный. Опускаю высоту `B_1T=sqrt(3)/2`
2)Прямые `B_1E`и `BE_1` являются диагоналями прямоугольника BB1EE1 и делятся в точке О пополам. `B_1O=sqrt(5)/2`
3) `sin<B_1OT=sqrt(15)/5`
В ответе `sin=sqrt(15)/10`
1) прямой `BD_1` и плоскостью `BCE_1`
2) прямой `B_1E` и плоскостью `BCE_1`
Решение:
Первая задача:
1) Находим точку пересечения `N` прямой `BD_1` и `(E_1C_1C)`. Линия пересечения находится из прямоугольного треугольника `DBD_1`
2) Из точки `N` опускаем пер-ляр `NO` на `(BCE_1)` (`NO=sqrt(3)/4`)
3) `sin<NBO=sqrt(3)/8`
Вторая задача:
1) Треугольник `BB_1F_1` прямоугольный. Опускаю высоту `B_1T=sqrt(3)/2`
2)Прямые `B_1E`и `BE_1` являются диагоналями прямоугольника BB1EE1 и делятся в точке О пополам. `B_1O=sqrt(5)/2`
3) `sin<B_1OT=sqrt(15)/5`
В ответе `sin=sqrt(15)/10`
Здравствуйте, помогите, пожалуйста, решить задачу по геометрии. Сколько думаю над ней, ничего не могу придумать. Вот задача:
В тэтраэдре DABC угол DAC = углу DAB и угол ADC = углу ADB.
Докажите, что BC перпендикулярно AD
Домашняя работа, ответ дайте, пожалуйста, до 24.00 по МСК. Заранее благодарю за помощь!
В тэтраэдре DABC угол DAC = углу DAB и угол ADC = углу ADB.
Докажите, что BC перпендикулярно AD
Домашняя работа, ответ дайте, пожалуйста, до 24.00 по МСК. Заранее благодарю за помощь!
Найти объем тела, ограничен поверхностью `(x^2+y^2+z^2)^3 = z^2/(x^2+y^2)`
Можно решать с помощью цилиндрической или сферической системы координат
цилиндрической или сферической если решать,то получим :
читать дальше
а как дальше делать не знаю.Помоги пожалуйста
Можно решать с помощью цилиндрической или сферической системы координат
цилиндрической или сферической если решать,то получим :
читать дальше
а как дальше делать не знаю.Помоги пожалуйста
Помогите, пожалуйста, решите эти задачи. Хотя бы напишите план действий и на какую теорию опираться. До среды, пожалуйста. Заранее благодарю:
1. Один конец данного отрезка лежит в плоскости альфа, а другой находитсяна расстоянии f см от неё. Найти расстояние от середины этого отрезка до плоскости альфа.
2. Из вершины прямоугольного равнобедренного треугольника АВС восставлен перпендикуляр АM к плоскости треугольника. Чему равно расстояние от точки M до гипотенузы этого треугольника, если АM= a, АВ=АС=n дм.
1. Один конец данного отрезка лежит в плоскости альфа, а другой находитсяна расстоянии f см от неё. Найти расстояние от середины этого отрезка до плоскости альфа.
2. Из вершины прямоугольного равнобедренного треугольника АВС восставлен перпендикуляр АM к плоскости треугольника. Чему равно расстояние от точки M до гипотенузы этого треугольника, если АM= a, АВ=АС=n дм.
Всё должно быть сделано настолько простым, насколько это возможно, но не проще. А. Энштейн
Что-то у меня не сходится, не понимаю, где косячу?
Задание: вычислить циркуляцию `vec a = (y - z, z - x, x - y)` по кривой:
`x = cos(t)`, `y = sin(t)`, `z = 2*(1 - cos(t))`
Понятно, что `0 <= t <= 2pi`
Вычислим через крив. инт. 1ого рода:
`C = int (vec a, vec t_0) dl`
`t = (-sin(t), cos(t), 2sin(t))`
`|t| = sqrt(1 + 4sin^2(t))`
`dl = sqrt(1 + 4sin^2(t))`
`=> C = int_(0)^(2pi) (-3 + 2sin(t) +2cos(t))dt = -6pi`
Но по Стоксу:
`C = intint (rot a, vec n_0) dS`
`rot a = (-2, -2, -2)`
Кривая - наклонённый эллипс, нормаль к нему: `vecn = (4, 0, 2)`
`vec n_0 = (2/sqrt(5), 0, 1/sqrt(5))`
Отсюда: `C = -6/sqrt(5) int int dS`
`S` - площадь эллипса. `S = pi*a*b = pi*sqrt(20)*2 = 4sqrt(5)*pi`
`=> C = -24*pi`
Вот в этом и печаль.
Задание: вычислить циркуляцию `vec a = (y - z, z - x, x - y)` по кривой:
`x = cos(t)`, `y = sin(t)`, `z = 2*(1 - cos(t))`
Понятно, что `0 <= t <= 2pi`
Вычислим через крив. инт. 1ого рода:
`C = int (vec a, vec t_0) dl`
`t = (-sin(t), cos(t), 2sin(t))`
`|t| = sqrt(1 + 4sin^2(t))`
`dl = sqrt(1 + 4sin^2(t))`
`=> C = int_(0)^(2pi) (-3 + 2sin(t) +2cos(t))dt = -6pi`
Но по Стоксу:
`C = intint (rot a, vec n_0) dS`
`rot a = (-2, -2, -2)`
Кривая - наклонённый эллипс, нормаль к нему: `vecn = (4, 0, 2)`
`vec n_0 = (2/sqrt(5), 0, 1/sqrt(5))`
Отсюда: `C = -6/sqrt(5) int int dS`
`S` - площадь эллипса. `S = pi*a*b = pi*sqrt(20)*2 = 4sqrt(5)*pi`
`=> C = -24*pi`
Вот в этом и печаль.
Межрегиональная олимпиада школьников «САММАТ» — ежегодная олимпиада по математике для всех желающих школьников 7–11-х классов. Историю «САММАТ» начали писать в 1993 году преподаватели Самарских ВУЗов, профессор Андреев А.А., профессор Соболев В.А. (Самарский государственный университет), профессор Радченко В.П. (Самарский государственный технический университет) при поддержке Самарского регионального отделения РАЕН (председатель – академик Астафьев В.И.). В организации и проведении последних олимпиад активное участие принимают призеры прошлых лет и выпускники ведущих Самарских вузов – Савин А.Н., д.т.н. Минаков И.В., к.ф.-м.н. Саушкин М.Н., к.ф.-м.н. Саушкин И.Н., к.ф.-м.н. Лыков К.В. к.ф.-м.н. Попов С.Ю., к.ф.-м.н. Лексина С.В., а также аспиранты и студенты старших курсов Самарских вузов.Первоначально в олимпиаде принимали участие школьники 8-11-х классов, с 1998 года добавился 7-й класс, а с 2010-2011 учебного года и учащиеся 6-х классов.
Ежегодно в «САММАТ» принимает участие более 1000 человек, из школ Самарской, Ульяновской, Оренбургской, Пензенской областей, республик Башкортостан, Мордовия, Татарстан.
Олимпиада «САММАТ», стала традиционной олимпиадой по математике при СамГУ и проводится в первое (второе) воскресенье марта (в 2011 году - 13 марта). В последние три года олимпиада «САММАТ» вошла в Перечень олимпиад школьников.
Олимпиада проводится в два этапа:
- первый этап — отборочный тур;
- второй этап — заключительный тур.
В заключительном туре олимпиады принимают участие победители и призеры отборочного тура.
Время на выполнение заданий первого этапа составляет 3 астрономических часа (180 минут), второго — 4 астрономических часа (240 минут).
Страница Олимпиады
Условия задач заключительного тура "САММАТ-2011"
На этой странице можно скачать:
Условия задач отборочного тура "САММАТ-2011" (с ответами)
Условия и решения задач "САММАТ-2010"(которые выдавались на олимпиаде)
Условия задач "САММАТ-2009" и "САММАТ-2008"
Условия и решения задач "САММАТ-2007"
Перечень рекомендуемой литературы для подготовки к олимпиаде «САММАТ»
2011 -11 класс Заключительный тур
► 1. Саушкин И.Н. Купил Роман раков, вчера - мелких, по цене 510 крон за штуку, а сегодня - по 990 крон, но очень крупных. Всего на раков он истратил 25200 крон, из них переплаты из-за отсутствия сдачи составили от 160 до 200 крон. Сколько Роман купил раков вчера и сколько сегодня, если крона - самая мелкая денежная единица?
► 2.Кузьмин Ю.Н. Решить систему уравнений
`6x+6y+6z=2xy+2yz+2zx+14=3xyz+18`
► 3. Лексина С.В. Докажите, что квадрат можно разрезать на 60 равных треугольников, из которых можно сложить 10 квадратов.
► 4. Гусев А.А. Пусть `a` действительная постоянная. Найдите все решения уравнения. При каких значениях параметра `a` уравнение четвертой степени `a^3x^4+2a^2x^2+x+a+1=0` имеет нечетное число действительных решений.
► 5. Лексина С.В. В единичном кубе `ABCDA_1B_1C_1D_1`, стоящем на грани `ABCD`, даны две точки `М` на ребре `AB`, `M_1` на ребре `A_1B_1`, такие, что `AM:MB=3:2`, a `A_1M_1:M_1B_1=2:3`. Муравей прополз по кратчайшем пути с постоянной скоростью из точки `M` в точку `M_1` так, что побывал во всех доступных гранях. Найти отношение скоростей муравья на горизонтальном участке и не на горизонтальных, если известно, что время, проведенное им на горизонтальных участках равно времени проведенному им на не горизонтальных участках.
► 6. Козлова Е. Найти функции `f(x)`,`g(x)`, `h(x)`, удовлетворяющие уравнению
`f(x+y)=g(x)+h(y)+xy(x+y+2011)`
и дифференцируемые в точке ноль.
► 7. Андреева Л. В. Брус размером 8 х 27 х 27 распилить на 4 части, из которых можно сложить куб.
► 8. Андреев А.А. Докажите, что число 9000001999 является составным.
► 9. Дворянинов С.В. Дан прямоугольник со сторонами 28 см и 12 см. Существует ли треугольная пирамида, у которой все грани равные треугольники и длина каждого ребра выражается целым числом сантиметров и развертка которой совпадает с этим прямоугольником? Если да, то нарисуйте эту развертку и укажите длины всех ребер пирамиды.
► 10. Андреев А.А. Пусть `[x]` - целая часть числа `x` - наибольшее целое число, не превосходящее `x`. Найдите наименьшее натуральное `m`, при котором найдется натуральное `n`, такое, что будет выполняться равенство
`[sqrt(m)]+[sqrt(m+1)]+...+[sqrt(n)]=2011`
UPD решения задач sammat.ru/files/sammat2011.pdf
Знаешь,когда цветочек стоит к тебе передом, не поворачивайся к нему задом. Потому что, когда повернешься - его может не оказаться!
читать дальше
При l=2, 2x1+x2=0
3x1+4x2-x3=0
приl=3, х1=0,
3х1+4х2-2х3=0
при l=1 х1=0
2х1 + 2х2=0
зх1+4х2=0
как далее?
При l=2, 2x1+x2=0
3x1+4x2-x3=0
приl=3, х1=0,
3х1+4х2-2х3=0
при l=1 х1=0
2х1 + 2х2=0
зх1+4х2=0
как далее?
Помогите решить пример: Найти целую часть числа 100^1/7
воскресенье, 13 марта 2011
`z=((2-2*i*sqrt(3))/(-4+4i))^8=((-1-sqrt(3))/4-i(1-sqrt(3))/4)^8`
`|z|=sqrt(x^2+y^2)=sqrt(2)/2`
`cos(a)=((-1-sqrt(3))sqrt(2))/8`
`sin(a)=((sqrt(3)-1)sqrt(2))/8`
Как будто получается не табличный угол... или я ошибся в расчётах?
`|z|=sqrt(x^2+y^2)=sqrt(2)/2`
`cos(a)=((-1-sqrt(3))sqrt(2))/8`
`sin(a)=((sqrt(3)-1)sqrt(2))/8`
Как будто получается не табличный угол... или я ошибся в расчётах?
Я одна, но всё же я есть. Я не могу сделать всё, но всё же могу сделать что-то. И я не откажусь сделать то немногое, что могу (c)
Данный топик продолжает раздел Электронные версии школьных учебников/задачников/дидактических материалов (часть 1)
Появление нового раздела связано с ограничением объема записей и комментариев на diary.
Топик создан для сбора ссылок на электронные версии материалов в помощь учителю.
Огромная благодарность всем, кто принимает в этом участие.
Внимание! Объем записи закончился. Продолжение здесь Электронные версии школьных учебников/задачников/дидактических материалов (часть 3) и здесь Электронные версии школьных учебников/задачников/дидактических материалов (часть 4)
Несколько книг из этого топика перенесены в тематические топики
См.:
В помощь учителю, учебники
Учебная и занимательная литература для студентов и школьников
Электронные версии школьных учебников/задачников/дидактических материалов (часть 1)
Электронные версии школьных учебников/задачников/дидактических материалов (часть 2)
Электронные версии школьных учебников/задачников/дидактических материалов (часть 3)
Электронные версии школьных учебников/задачников/дидактических материалов (часть 4)
См. также:
В помощь учителю, учебники
Учебная и занимательная литература для студентов и школьников
Появление нового раздела связано с ограничением объема записей и комментариев на diary.
Топик создан для сбора ссылок на электронные версии материалов в помощь учителю.
Огромная благодарность всем, кто принимает в этом участие.
Внимание! Объем записи закончился. Продолжение здесь Электронные версии школьных учебников/задачников/дидактических материалов (часть 3) и здесь Электронные версии школьных учебников/задачников/дидактических материалов (часть 4)
Несколько книг из этого топика перенесены в тематические топики
См.:
В помощь учителю, учебники
Учебная и занимательная литература для студентов и школьников
Газета "Математика (1 сентября)
| Номера газеты | Размер, характер файла | Ссылка для скачивания | Зеркало |
| Математика за 2007 (№1-24) Спасибо Ak-sakal |
djvu/rar, 45,56 mb | rghost | ifolder.ru |
| Математика за 2008 (№1-24) Cпасибо fihtengolts |
djvu/rar, 21 mb | rghost | ifolder.ru |
| Математика за 2009 (№1-24) Cпасибо Ak-sakal |
djvu/rar, 34 Мб | rghost | ifolder.ru |
| Математика за 2010 (№1-11) Cпасибо Ak-sakal |
djvu/rar, 28.89 Мб | rghost | ifolder.ru | Математика № 12 2010 Cпасибо Гостю |
djvu, 1,4 Мб | ifolder | rghost |
| Математика за 2010 (№13-24) Cпасибо fihtengolts |
djvu/rar, 19.19 Мб | rghost | ifolder.ru |
| Математика №№ 1-4 2011 Источник rutracker.org |
pdf/rar, 36 Мб | narod.ru | rghost |
| Отдельно Математика №№ 1-3 2011 Источник rutracker.org |
pdf /rar, 30.94 Мб | ifolder.ru | mediafire.com |
| Математика № 4 2011 Источник rutracker.org |
pdf /rar, 5,74 Мб | ifolder.ru | mediafire.com |
| Математика №№ 5-8 2011 rutracker.org |
pdf/rar, 30 Мб | rghost.ru |
ifolder.ru |
| Математика № 9 2011 | pdf/rar (4.57 Мб - с текстовым слоем) | rghost.ru |
ifolder.ru |
| djvu/rar (2,33 Мб - без оcr, поиск и копирование невозможны) | rghost.ru |
ifolder.ru | |
| Математика № 10 2011 | pdf/rar (3.56 Мб - с текстовым слоем) | rghost.ru |
ifolder.ru |
| djvu/rar (2,33 Мб - без оcr, поиск и копирование невозможны) | rghost.ru |
ifolder.ru | |
| Математика № 11 2011 | pdf/rar (4.79 Мб - с текстовым слоем) | rghost.ru |
ifolder.ru |
| djvu/rar (2.44 Мб - без оcr, поиск и копирование невозможны) | rghost.ru |
ifolder.ru | |
| Математика № 12 2011 | pdf/rar (7 Мб - с текстовым слоем) | rghost.ru |
ifolder.ru |
| djvu/rar (3 Мб - без оcr, поиск и копирование невозможны) | rghost.ru |
ifolder.ru |
Электронные версии школьных учебников/задачников/дидактических материалов (часть 1)
Электронные версии школьных учебников/задачников/дидактических материалов (часть 2)
Электронные версии школьных учебников/задачников/дидактических материалов (часть 3)
Электронные версии школьных учебников/задачников/дидактических материалов (часть 4)
См. также:
В помощь учителю, учебники
Учебная и занимательная литература для студентов и школьников
`lim_(x->+oo) (x^(lnx)) /(lnx) `
Числитель - бесконечность в степени бесконечности = бесконечность?
Знаменатель - бесконечность?
Т.е. можно сразу применить правило Лопиталя? Или тут надо преобразовать как то сначала
Числитель - бесконечность в степени бесконечности = бесконечность?
Знаменатель - бесконечность?
Т.е. можно сразу применить правило Лопиталя? Или тут надо преобразовать как то сначала
You trust me... I'm a devil.
Вот несколько примеров, которые не могу решить (интересуют под буквами а, в, г, особенно в и г)
Под а) я там подставила просто 1, и получилось что ноль делится на ноль, можно ли так?
Под в) произвела некоторые действия и пришла к такому: lim (xcos (1/x) - 1)/x
Под г) вообще ничего не получается
Нужно до завтрашнего утра, прошу помощи)
вот сами примеры:
помогитеее)
Под а) я там подставила просто 1, и получилось что ноль делится на ноль, можно ли так?
Под в) произвела некоторые действия и пришла к такому: lim (xcos (1/x) - 1)/x
Под г) вообще ничего не получается
Нужно до завтрашнего утра, прошу помощи)
вот сами примеры:
помогитеее)
