Докажите,что уравнение n!-n=k^2 неразрешимо в натуральных числах n и k.
(Пробовала методом индукции не получилось )
(Пробовала методом индукции не получилось )
суббота, 07 апреля 2012
Everything is gonna be alright! Everything is gonna be alright! Everything is gonna be alright! Be strong believe!
Здравствуйте, вот такая вот проблема по ТФКП.
Задача: a) Найти образ области Z={-3 < Im(z) < 1} под действием функции w=2i*z+1-i
б) Найти функцию w=f(z), осуществляющую отобржение Z->W, если Z={Re(z)<1}, W={|w|>2}
Задачи по идее не очень сложные, но я совершенно не понимаю все, что связано с образами и отображением, так что не могли бы вы помочь или посоветовать учебник, где это все хорошо и понятно расписано?
Пример из учебника Мордковича за 11 класс
sin x*sin y=-1/2
tg x*ctg y=1
из второго уравнения пришла к уравнению sin(x-y)=0
отсюда следует что x-y=Pi n?
просто в решении из методички это уравнение имеет два решения x-y=2pi n и x-y=pi+2pi n, почему такие решения?) из них ответ выходит правильный
вот из самой методички скрин читать дальше
пятница, 06 апреля 2012
Приведу способ решения log неравенства с помощью тождества, которое давали нам в классе log_a (g)-log_a (f) V 0 => g-f V 0
Может, тут какой-то особый случай, что можно эту формулу применять? Помогите разобраться
`log_(1-(x^2)/26) (x^2+10x+26) >= log_(1+(x^2)/26) (x^2+10x+26)`
Может, тут какой-то особый случай, что можно эту формулу применять? Помогите разобраться
`log_(1-(x^2)/26) (x^2+10x+26) >= log_(1+(x^2)/26) (x^2+10x+26)`
Добрый день! Посоветуйте пожалуйста литературу где хорошо расписана теория на тему неявных функций, условный экстремум, метод лагранжа, метод Гисеянна ( фамилию только на слух запомнил), при этом обязательно были разобраны ( хотя бы несколько) задачи на эти темы?
Скорость моторной лодки по течению реки больше 21 км/ч и меньше 23 км/ч, а скорость против течения больше 19 км/ч и меньше 21 км/ч. В каком промежутке будет собственная скорость( в стоячей воде) лодки?
найти в точке А полный дифференциал функции заданной неявно sin(xy)=x*tg(z-p/4) A(1,0,p/4)
Я примерно представляю как решать: наити прозводные z по x, z по y потом подставить значения из точки А в полученное.
Тут то и начинается загвоздка я не могу продифференцировать z по x, а z по y =-x*cos(xy)?
Я примерно представляю как решать: наити прозводные z по x, z по y потом подставить значения из точки А в полученное.
Тут то и начинается загвоздка я не могу продифференцировать z по x, а z по y =-x*cos(xy)?
Как доказать, что выражение `x^2*z+y^2*x=z^2*y` не имеет решения в натуральных числах???
Задача (из книги Практикум по элементарной математике Литвиненко, Мордкович. Геометрия)
Площадь боковой поверхности правильной 4-х угольной пирамиры равна Q, а двухгранный угол при ребре основания равен "альфа". Найти расстояние между центроидом основания и плоскостью боковой грани пирамиды.
Площадь боковой поверхности правильной 4-х угольной пирамиры равна Q, а двухгранный угол при ребре основания равен "альфа". Найти расстояние между центроидом основания и плоскостью боковой грани пирамиды.
Товаровед плодоовощной базы определяет сорт поступившей от постоянного поставщика партии яблок. Известно, что в среднем 40% выращенного поставщиком урожая составляют яблоки первого сорта. Вероятность того, что товаровед признает первосортную партию первым сортом, равна 0,85. Кроме того, он может допустить ошибку, сочтя непервосортную партию первосортной, с вероятностью 0,2. Какова вероятность того, что он неверно установит сорт партии яблок?
Решая неравенство, сократил его до (начальное ОДЗ x != (-3; -2; -1; 0))
`log_(x^2+6x+10) (log_(2x^2+2x+3) (x^2-2x)) >= 0`
Перейдем к десятичному основанию
( lg ((lg (x^2-2x)) / (lg (2x^2+2x+3)) ) / (lg (x^2+6x+10)) >= 0
Разложим дробь из числителя по тождеству
( lg ((lg (x^2-2x)) - (lg (2x^2+2x+3)) ) / (lg (x^2+6x+10)) >= 0
По свойству log_a (b) - log_c (d) = b-d разложим
( ( lg (x^2-2x) - lg (2x^2+2x+3) ) / (lg (x^2+6x+10)) ) >= 0
Повторно применим свойство
( ( (x^2-2x)-(2x^2+2x+3) ) / ((x^2+6x+10) - 1) ) >= 0
( (-x^2-4x-3)/(x^2-6x+9) ) >= 0
(-(x+3)(x+1))/(x-4)*(x-2)) >=0
Таким образом, ответ x in (-inf ;-3) U (-2;-1) U (2;4)
Где наврал?
`log_(x^2+6x+10) (log_(2x^2+2x+3) (x^2-2x)) >= 0`
Перейдем к десятичному основанию
( lg ((lg (x^2-2x)) / (lg (2x^2+2x+3)) ) / (lg (x^2+6x+10)) >= 0
Разложим дробь из числителя по тождеству
( lg ((lg (x^2-2x)) - (lg (2x^2+2x+3)) ) / (lg (x^2+6x+10)) >= 0
По свойству log_a (b) - log_c (d) = b-d разложим
( ( lg (x^2-2x) - lg (2x^2+2x+3) ) / (lg (x^2+6x+10)) ) >= 0
Повторно применим свойство
( ( (x^2-2x)-(2x^2+2x+3) ) / ((x^2+6x+10) - 1) ) >= 0
( (-x^2-4x-3)/(x^2-6x+9) ) >= 0
(-(x+3)(x+1))/(x-4)*(x-2)) >=0
Таким образом, ответ x in (-inf ;-3) U (-2;-1) U (2;4)
Где наврал?
(1+x)*(1+3x)^(1/5)
Пробовал разложить правый множитель, а затем домножить получившийся ряд на первый. Получился ряд, но он не степенной ((
Пробовал разложить правый множитель, а затем домножить получившийся ряд на первый. Получился ряд, но он не степенной ((
`log_(3x-3) 3+log_(x-1)^2 27 >= 27`
<=>
`( (log_3 3)/(log_3 3+log_3 (x-1)) + (log_3 27)/(2*log_3 (x-1)) ) >=2
<=>
`( 1/ (1+log_3 (x-1)) + 3/(2*log_3 (x-1) ) >=2`
` ( 1/log3 (x-1)+ 3/(2log_3 (x-1) )>=1`
log_3 (x-1) = t
Ограничения?
t<>0
(1/t)+(3/2t)-1>=0
(2+3-2t)/2t>=0
t in (0;5/2)
До этого момента правильно?
<=>
`( (log_3 3)/(log_3 3+log_3 (x-1)) + (log_3 27)/(2*log_3 (x-1)) ) >=2
<=>
`( 1/ (1+log_3 (x-1)) + 3/(2*log_3 (x-1) ) >=2`
` ( 1/log3 (x-1)+ 3/(2log_3 (x-1) )>=1`
log_3 (x-1) = t
Ограничения?
t<>0
(1/t)+(3/2t)-1>=0
(2+3-2t)/2t>=0
t in (0;5/2)
До этого момента правильно?
1. В ящике 10 мячей, 6 из них новых. Для первой игры из коробки берут 2 мяча. После игры их кладут назад. Для второй игры также берут 2 мяча. Какова вероятность что для второй игры взяты новые мячи?
`(6/10*2)*2`
2. Получая товар на склад проверяются случаайео выбраных 4 предмета. Составьте закон разложения если вероятность нахождения нестандартного премета 10%. Найдите среднее значение, депрессию и стандартное отклонение.
3. Дано закон разложения сулчайного дискретного значения `x`:
`X` 1 2 4 5
`P` 0.31 0.1 0.29 0.3
(не знаю как тут рисуются таблицы)
Найти среднее значение, дипрессисю и стандартное отклонение.
ЗЫ Не решите, а укажите где и как об этом написано, как решать...
`(6/10*2)*2`
2. Получая товар на склад проверяются случаайео выбраных 4 предмета. Составьте закон разложения если вероятность нахождения нестандартного премета 10%. Найдите среднее значение, депрессию и стандартное отклонение.
3. Дано закон разложения сулчайного дискретного значения `x`:
`X` 1 2 4 5
`P` 0.31 0.1 0.29 0.3
(не знаю как тут рисуются таблицы)
Найти среднее значение, дипрессисю и стандартное отклонение.
ЗЫ Не решите, а укажите где и как об этом написано, как решать...
Здравствуйте!Я не могу решить эту задачу,помогите пожалуйста.
Две стороны треугольника равны 2 и 10,а угол между ними равен 45 градусов.Нужно найти его площадь.
Две стороны треугольника равны 2 и 10,а угол между ними равен 45 градусов.Нужно найти его площадь.
Здравствуйте!
Подскажите пожалуйста каким методом решать задачу:
Найти вероятность того, что для данных 30 человек 6 из 12 месяцев года содержат по два дня рождения и 6 - по три.
Подскажите пожалуйста каким методом решать задачу:
Найти вероятность того, что для данных 30 человек 6 из 12 месяцев года содержат по два дня рождения и 6 - по три.
Всем привет.
Требуется немного вашей помощи, товарищи Большую часть я решил, но есть и вопросы... Ах да, проверьте решенное, если не сложно.
1) Дан закон распределения случайной величины х
х -1 0 1 2
p 0.1 0.4 0.2 k
Найти к, функцию распределения случайной величины `x^2, M (x^2), D (x^2), p(х<=3)`
Решение:
`1) к= 1-(0.1+0.4+0.2) = 0.3
2) х^2 0 1 4
p 0.4 0.3 0.3
`а) x<= 0 p=0`
`б) 0<= x <= 1 p(0) = 0.4`
`в) 1<= x <= 4 p(0)+p(1) = 0.7`
`г) x>= 4 p(0)+p(1)+p(4)= 1`
`F(x^2) =`
`0, x<= 0`
`0.4, 0<= x <= 1`
`0.7, 1<= x <= 4`
`1, x>= 4`
`3) M (x^2) = 0+0.3+4*0.3 = 1.5`
`M (x) = 0.7`
`M (x^4) = 16.3`
`4) D (x^2) = M(x^4) - M(x^2) ^2 = 14.05`
`5) p(х<=3) = F(b) = F(3) = 0.7`
Задание 2:
<читать дальше
Случайная величина х имеет плотность распределения:
`f(x) = { ( a/(pi*sqrt(c^2 - x^2) ) \ \ ; \ \ -c < x < c), ( 0 \ \ \ ; \ \ |x| >= c) :}`
Найти a, М, Д, ФР, P(-c/2<x<0)
Требуется немного вашей помощи, товарищи Большую часть я решил, но есть и вопросы... Ах да, проверьте решенное, если не сложно.
1) Дан закон распределения случайной величины х
х -1 0 1 2
p 0.1 0.4 0.2 k
Найти к, функцию распределения случайной величины `x^2, M (x^2), D (x^2), p(х<=3)`
Решение:
`1) к= 1-(0.1+0.4+0.2) = 0.3
2) х^2 0 1 4
p 0.4 0.3 0.3
`а) x<= 0 p=0`
`б) 0<= x <= 1 p(0) = 0.4`
`в) 1<= x <= 4 p(0)+p(1) = 0.7`
`г) x>= 4 p(0)+p(1)+p(4)= 1`
`F(x^2) =`
`0, x<= 0`
`0.4, 0<= x <= 1`
`0.7, 1<= x <= 4`
`1, x>= 4`
`3) M (x^2) = 0+0.3+4*0.3 = 1.5`
`M (x) = 0.7`
`M (x^4) = 16.3`
`4) D (x^2) = M(x^4) - M(x^2) ^2 = 14.05`
`5) p(х<=3) = F(b) = F(3) = 0.7`
Задание 2:
<читать дальше
Случайная величина х имеет плотность распределения:
`f(x) = { ( a/(pi*sqrt(c^2 - x^2) ) \ \ ; \ \ -c < x < c), ( 0 \ \ \ ; \ \ |x| >= c) :}`
Найти a, М, Д, ФР, P(-c/2<x<0)
При каких положительных значениях параметра a выполняется неравенство `int_0^a (3x^2 - 4x + 2)dx <= a`?
Я одна, но всё же я есть. Я не могу сделать всё, но всё же могу сделать что-то. И я не откажусь сделать то немногое, что могу (c)
Небольшой отчет за март 2012.
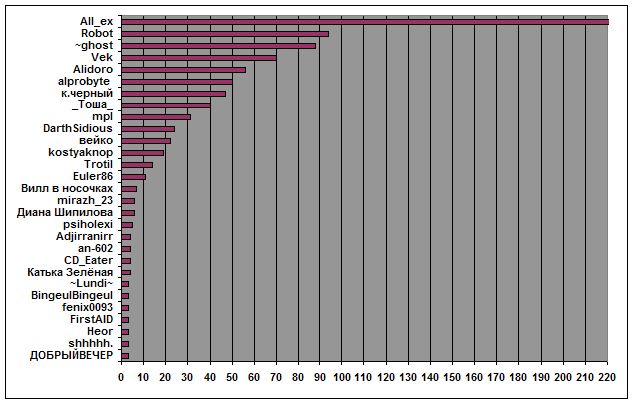
В марте нас посетило 274010 человек. Появилось 676 новых записей.
Наиболее активно помогали All_ex Robot ~ghost VEk Alidoro alprobyte к.черный _ТошА_ mpl DarthSidious вейко kostyaknop Trotil Euler86 Вилл в носочках mirazh_23 Диана Шипилова psiholexi Adjirranirr an-602 CD_Eater Катька Зелёная ~Lundi~ BingeulBingeul fenix0093 FirstAID Heor shhhhh. ДОБРЫЙВЕЧЕР
Традиционная диаграмма
С резким отрывом от остальных лидирует All_ex ! Поздравляем!!!!
Второе место поделили ~ghost и Robot
На третьем месте VEk
Спасибо за помощь в марте и Ak-sakal atlant-e Prepod UnionJack Кицуне Alerr anuuta cherepasha forgotten thing LaBalance. mad-math PMtime webmath yonkis Груша Вильямс Омон Ра
Гости помогли в решении 29 задач.
Спасибо членам сообщества, которые делились информацией, ссылками на статьи и ресурсы.
Спасибо тем, кто выкладывал книги: Ak-sakal pemac Yri kostyaknop Alidoro Гости Robot и др.
Спасибо вейко Alidoro DarthSidious All_ex за выкладываемые интересные задачи.
Может быть вы пропустили:
1)в связи с ограничением объема предыдущего раздела появился новый раздел: Электронные версии школьных учебников/задачников/дидактических материалов (часть 5)
2) создан новый тег Тренировочные/диагностические работы
3) в запись Пробный (репетиционный) экзамен по математике 17 марта 2012 г. добавлены четыре полных варианта пробника (Москва) с ответами. (Онлайн тестирование можно пройти на сайтах test.mioo.ru и mioo.cde.ru)
Для любителей головоломок книга известных авторов:
В марте нас посетило 274010 человек. Появилось 676 новых записей.
Наиболее активно помогали All_ex Robot ~ghost VEk Alidoro alprobyte к.черный _ТошА_ mpl DarthSidious вейко kostyaknop Trotil Euler86 Вилл в носочках mirazh_23 Диана Шипилова psiholexi Adjirranirr an-602 CD_Eater Катька Зелёная ~Lundi~ BingeulBingeul fenix0093 FirstAID Heor shhhhh. ДОБРЫЙВЕЧЕР
Традиционная диаграмма
С резким отрывом от остальных лидирует All_ex ! Поздравляем!!!! Второе место поделили ~ghost и Robot На третьем месте VEk Спасибо за помощь в марте и Ak-sakal atlant-e Prepod UnionJack Кицуне Alerr anuuta cherepasha forgotten thing LaBalance. mad-math PMtime webmath yonkis Груша Вильямс Омон Ра
Гости помогли в решении 29 задач.
Спасибо членам сообщества, которые делились информацией, ссылками на статьи и ресурсы.
Спасибо тем, кто выкладывал книги: Ak-sakal pemac Yri kostyaknop Alidoro Гости Robot и др.
Спасибо вейко Alidoro DarthSidious All_ex за выкладываемые интересные задачи.
Огромная благодарность от лица сообщества всем помогающим!!!
Может быть вы пропустили:
1)в связи с ограничением объема предыдущего раздела появился новый раздел: Электронные версии школьных учебников/задачников/дидактических материалов (часть 5)
2) создан новый тег Тренировочные/диагностические работы
3) в запись Пробный (репетиционный) экзамен по математике 17 марта 2012 г. добавлены четыре полных варианта пробника (Москва) с ответами. (Онлайн тестирование можно пройти на сайтах test.mioo.ru и mioo.cde.ru)
Для любителей головоломок книга известных авторов:
 |
Нестеренко, Ю. В., С. Н. Олехник, М. К. Потапов Задачи на смекалку 2-е изд. - М. : Дрофа, 2005. — 233, [7] с.: ил. — (Познавательно! Занимательно!). ISBN 5-7107-9270-5 В книге собраны задачи занимательного характера, популярные в России в начале XX века. Авторы переработали условия многих задач, придав им современный вид или стилизуя под старинные истории и сказки. Занимательные сюжеты будут интересны как детям, так и взрослым. Переформатировано из исходника (221 мб) Скачать (djvu/rar+ocr, 3.45 Мб) ifolder.ru|| mediafire |
Успеха всем в апреле! Надеюсь, что весна наконец-то вступит в свои права!