2x(tgx)^x^2(ln(tgx)+(x/sin2x))
среда, 27 января 2016
вторник, 26 января 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Дана плоская фигура с площадью равной `A > n`, где `n` - положительное целое число. Докажите, что фигуру можно поместить на координатной плоскости так, чтобы она накрывала по крайней мере `(n + 1)` точку с целыми координатами. |  |
понедельник, 25 января 2016
Простыми словами
В день Татьяны все студенты пьяны!
Дорогие студенты и не менее дорогие бывшие студенты и преподаватели! От всей души поздравляю вас с практически профессиональным праздником
Вставлю из прошлогодних поздравлений.
Почему студенты отмечают Татьянин день?
читать дальше
Простыми словами
Если бы я был богат, возможно, я не посвятил бы себя математике.
Жозеф Луи Лагранж
Сегодня исполнилось 280 лет со дня рождения Жозефа Луи Лагранжа.
Это картинка из Яндекса:
Она изображает точки Лагранжа:
Точки Лагранжа и эквипотенциальные поверхности системы двух тел (с учётом центробежного потенциала)
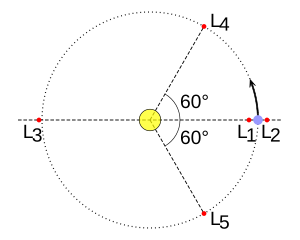
Схема пяти лагранжевых точек в системе двух тел, когда одно тело намного массивнее другого (Солнце и Земля). В такой системе точки L3, L4, L5 показаны на самой орбите, хотя фактически они будут находиться немного за ней
Топик в сообществе
Жозеф Луи Лагранж
Сегодня исполнилось 280 лет со дня рождения Жозефа Луи Лагранжа.
Это картинка из Яндекса:
Она изображает точки Лагранжа:
Точки Лагранжа и эквипотенциальные поверхности системы двух тел (с учётом центробежного потенциала)
Схема пяти лагранжевых точек в системе двух тел, когда одно тело намного массивнее другого (Солнце и Земля). В такой системе точки L3, L4, L5 показаны на самой орбите, хотя фактически они будут находиться немного за ней
Топик в сообществе
Ищу литературу и интернет ресурсы с заданиями различных вузовских студенческих олимпиад по математике.
P.S. С заданиями олимпиады МФТИ знаком.
P.S. С заданиями олимпиады МФТИ знаком.
воскресенье, 24 января 2016
Написать формулу общего члена ряда
`1+(1*3)/(1*4)+(1*3*5)/(1*4*7)+(1*3*5*7)/(1*4*7*10)+...`
С числителем проблем нет. Это факториал всех нечетных чисел, т.е.
`sum_(n=0)^infty (2n-1)!!`
А как записать знаменатель? Это произведение чисел с шагом три. Но если записать факториал, то он будет подразумевать произведение всех чисел.
Как это записать математически? Прошу помощи.
`1+(1*3)/(1*4)+(1*3*5)/(1*4*7)+(1*3*5*7)/(1*4*7*10)+...`
С числителем проблем нет. Это факториал всех нечетных чисел, т.е.
`sum_(n=0)^infty (2n-1)!!`
А как записать знаменатель? Это произведение чисел с шагом три. Но если записать факториал, то он будет подразумевать произведение всех чисел.
Как это записать математически? Прошу помощи.
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Существует ли такая окружность и такое бесконечное множество точек на ней, что расстояние между любыми двумя точками из этого множества является рациональным? | |
пятница, 22 января 2016
Значит дана такая функция
`u = zln(z) - z - z ln(xy) + xy + x^2+ 2y^2 - 4x - 2y`
Знаю, что надо составить систему уравнений из частных производных по всем аргументам и приравнять их к 0. Но тут очень страшные получаются частные производные. Я что-то не могу найти идею, как решить данную систему:
`(\delta u)/(\delta x) = -z/x + y + 2x - 4 = 0`
`(\delta u)/(\delta y) = -z/y + x + 4y - 2 = 0`
`(\delta u)/(\delta z) = ln(z) - ln(xy) = 0`
Может я частные производные неверно нашел. Просто как-то с логарифмами система вообще не идет.
Еще, если можно было бы ее привести сразу к квадратичной форме, то можно было бы сразу пользоваться критерием Сильвестра. Но ее видимо никак сразу так не привести к квадратичной форме. Опять логарифмы мешают. Просто ступор. Есть ли какие-то другие способы исследовать на экстремум эту функцию?
`u = zln(z) - z - z ln(xy) + xy + x^2+ 2y^2 - 4x - 2y`
Знаю, что надо составить систему уравнений из частных производных по всем аргументам и приравнять их к 0. Но тут очень страшные получаются частные производные. Я что-то не могу найти идею, как решить данную систему:
`(\delta u)/(\delta x) = -z/x + y + 2x - 4 = 0`
`(\delta u)/(\delta y) = -z/y + x + 4y - 2 = 0`
`(\delta u)/(\delta z) = ln(z) - ln(xy) = 0`
Может я частные производные неверно нашел. Просто как-то с логарифмами система вообще не идет.
Еще, если можно было бы ее привести сразу к квадратичной форме, то можно было бы сразу пользоваться критерием Сильвестра. Но ее видимо никак сразу так не привести к квадратичной форме. Опять логарифмы мешают. Просто ступор. Есть ли какие-то другие способы исследовать на экстремум эту функцию?
среда, 20 января 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Рассмотрим многочлен с неотрицательными действительными коэффициентами `p(x) = a_0 + a_1*x + ... + a_n*x^n`. Предположим, что `p(4) = 2` и `p(16) = 8`. Докажите, что `p(8) <= 4` и найдите, с доказательством, все такие многочлены, для которых `p(8) = 4`. |  |
вторник, 19 января 2016
Исследовать на сходимость ряд
`sum_(n=1)^(infty) (arctg ((1+(-1)^n)/2)n)/(n^3+2)`
Если `n` - четное, то `(-1)^n=1` и числитель имеет вид `arctg (n)`.
Если `n` - нечетное, то `(-1)^n=-1` и числитель равен нулю.
Получается, что этот ряд не является знакочередующимся. Напрашивается признак сравнения. Но я не понимаю, как к нему подойти.
`sum_(n=1)^(infty) (arctg ((1+(-1)^n)/2)n)/(n^3+2)`
Если `n` - четное, то `(-1)^n=1` и числитель имеет вид `arctg (n)`.
Если `n` - нечетное, то `(-1)^n=-1` и числитель равен нулю.
Получается, что этот ряд не является знакочередующимся. Напрашивается признак сравнения. Но я не понимаю, как к нему подойти.
понедельник, 18 января 2016
Step by step ...
Задания муниципального этапа по математике 2015-2016 учебного года
01 Республика Адыгея
Республиканская естественно-математическая школа
04 Республика Алтай
22 Алтайский край
Видеоразборы заданий муниципального этапа по математике
28 Амурская область
29 Архангельская область
Образование Архангельской области
30 Астраханская область
02 Республика Башкортостан
Отдел образования г. Октябрьский
31 Белгородская область
32 Брянская область
Отдел образования Дубровского района
03 Республика Бурятия
33 Владимирская область
Управление образования администрации муниципального образования Судогодский район
34 Волгоградская область
35 Вологодская область
36 Воронежская область
05 Республика Дагестан
79 Еврейская автономная область
75 Забайкальский край
06 Республика Ингушетия
37 Ивановская область
Региональный портал Ивановской области
38 Иркутская область
Образовательный портал г. Братска
07 Кабардино-Балкарская Республика
39 Калининградская область
08 Республика Калмыкия
40 Калужская область
Отдел образования Малоярославецкой районной администрации
41 Камчатский край
09 Карачаево-Черкесская Республика
10 Республика Карелия
Информационно-методический центр г. Олонец
42 Кемеровская область
Управление образования г. Юрги
43 Кировская область
11 Республика Коми
44 Костромская область
Образовательный портал Костромской области
23 Краснодарский край
Центр дополнительного образования для детей
24 Красноярский край
Информационно-методический центр г. Шарыпово
91 Республика Крым
45 Курганская область
46 Курская область
47 Ленинградская область
48 Липецкая область
49 Магаданская область
12 Республика Марий Эл
13 Республика Мордовия
Республиканский лицей
77 Москва
Московский центр непрерывного математического образования
50 Московская область
Региональный центр поддержки олимпиадного движения
51 Мурманская область
83 Ненецкий автономный округ
52 Нижегородская область
Департамент образования г. Саров
53 Новгородская область
54 Новосибирская область
55 Омская область
Портал региональной системы выявления и развития молодых талантов
56 Оренбургская область
57 Орловская область
58 Пензенская область
59 Пермский край
Региональные олимпиады Пермского края
25 Приморский край
60 Псковская область
61 Ростовская область
62 Рязанская область
Олимпиады школьников г. Рязани
63 Самарская область
78 Санкт-Петербург
64 Саратовская область
14 Республика Саха (Якутия)
65 Сахалинская область
66 Свердловская область
Дворец детского и юношеского творчества г. Нижний Тагил
15 Республика Северная Осетия — Алания
67 Смоленская область
26 Ставропольский край
68 Тамбовская область
16 Республика Татарстан
Электронное образование в Республике Татарстан
69 Тверская область
70 Томская область
71 Тульская область
17 Республика Тыва
72 Тюменская область
18 Удмуртская Республика
Центр столичного образования, г. Ижевск
73 Ульяновская область
27 Хабаровский край
19 Республика Хакасия
86 Ханты-Мансийский автономный округ — Югра
Департамент образования Нефтеюганского района
74 Челябинская область
Олимпийский портал
20 Чеченская Республика
21 Чувашская Республика
87 Чукотский автономный округ
89 Ямало-Ненецкий автономный округ
Департамент образования г. Салехард
76 Ярославская область
Межшкольный методический центр Угличского района
Обновления
2016.02.05 Добавлена информация по Удмуртской Республике.
воскресенье, 17 января 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Докажите, что среди любых десяти последовательных целых чисел найдется одно число, которое будет взаимно простым с остальными числами. Например, рассмотрим числа `114`, `115`, `116`, `117`, `118`, `119`, `120`, `121`, `122`, `123`. Числа `119` и `121` будут взаимно просты с остальными числами. [Два целых числа `a`, `b` называются взаимно простыми если их наибольший общий делитель равен единице.] | |
пятница, 15 января 2016
Как перемещается точка 1/z когда z описывает
окружность с центром в точке a+bi и с радиусом г? Мои рассуждения: z=(a+bi)+r(cos Ф+ isin Ф), где Ф - любое вещ. число, точка же вращается. Тогда точка 1/z вращается по окружности с центром в точке (a-bi)/a^2+b^2+r^2+2r(a cos Ф + b sin Ф) c радиусом r/a^2+b^2+r^2+2r(a cos Ф + b sin Ф). Фигня какая-то получилась. Если принять, что cos Ф=a/sqrt(a^2+b^2) , a sin Ф=b/sqrt(a^2+b^2) , то что-то выходит, но ведь точка же вращается!!!
окружность с центром в точке a+bi и с радиусом г? Мои рассуждения: z=(a+bi)+r(cos Ф+ isin Ф), где Ф - любое вещ. число, точка же вращается. Тогда точка 1/z вращается по окружности с центром в точке (a-bi)/a^2+b^2+r^2+2r(a cos Ф + b sin Ф) c радиусом r/a^2+b^2+r^2+2r(a cos Ф + b sin Ф). Фигня какая-то получилась. Если принять, что cos Ф=a/sqrt(a^2+b^2) , a sin Ф=b/sqrt(a^2+b^2) , то что-то выходит, но ведь точка же вращается!!!
Добрый день!
Помогите, пожалуйста, разобраться с задачей.
36 карт розданы 4 игрокам по 6 карт каждому, а 12 лежат в прикупе. Найти вероятность того, что все тузы окажутся у первого игрока.
Чтобы найти вероятность, нужно использовать классическое определение вероятности P=m/n? Или другие формулы?
Не очень понимаю, что делать с прикупом(
Помогите, пожалуйста, разобраться с задачей.
36 карт розданы 4 игрокам по 6 карт каждому, а 12 лежат в прикупе. Найти вероятность того, что все тузы окажутся у первого игрока.
Чтобы найти вероятность, нужно использовать классическое определение вероятности P=m/n? Или другие формулы?
Не очень понимаю, что делать с прикупом(
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Для всех натуральных чисел `n` найдите (с доказательством) все натуральные числа `m`, для которых существуют натуральные числа `x_1 < x_2 < ... < x_n`, удовлетворяющие равенству `1/(x_1)+2/(x_2)+ ... n/(x_n) = m`. | |
понедельник, 11 января 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Четырехугольник `ABCD` вписан в окружность радиуса `R`. Обозначим длины сторон `ABCD` как `a`, `b`, `c`, `d` и пусть площадь `ABCD` равна `Q`. Докажите, что `R^2 =((a*b + c*d)*(a*c + b*d)*(a*d + b*c))/(16*Q^2)`. Докажите, что `R >= ((a*b*c*d)^(3/4))/(Q*sqrt(2))` и что равенство достигается тогда и только тогда, когда `ABCD` является квадратом. | |
воскресенье, 10 января 2016
Как доказать, что произведение матрицы на обратную к ней матрицу коммутативно? Или данное утверждение вытекает из определения обратной матрицы и не требует доказательства?
суббота, 09 января 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Докажите, что для всех действительных чисел `x >= 0`, `y >= 0`, `x + y = 2` выполняется неравенство `x^2*y^2*(x^2 + y^2) <= 2`. | |
пятница, 08 января 2016
Простыми словами
Главный враг знания — не невежество, а иллюзия знания. Стивен Хокинг |
Сегодня день рождения Стивена Хокинга. Ему исполнилось 74 года! Пожелаем ему крепкого здоровья и всего того, чего он сам себе хочет пожелать. (А это, насколько я понимаю, космическое путешествие))
Википедия
Стивен Уильям Хокинг (англ. Stephen William Hawking, род. 8 января 1942, Оксфорд, Великобритания) — английский физик-теоретик. Учился в Оксфорде, затем в Кембридже, где стал профессором математики. Изучал теорию возникновения мира в результате Большого взрыва, а также теорию чёрных дыр. Высказал гипотезу, что маленькие чёрные дыры теряют энергию, испуская излучение Хокинга, и, в конце концов, «испаряются». Популяризатор науки.
Биография
Стивен Хокинг родился 8 января 1942 года в Оксфорде, куда переехали из Лондона его родители, опасаясь бомбёжек немецкой авиации.
Отец — Фрэнк Хокинг, работавший исследователем в медицинском центре в Хампстеде. Мать, Изабель Хокинг, работала там же секретарём. В семье, кроме Стивена, воспитывались две младшие сестры — Филипа и Мэри, и усыновлённый брат Эдвард.
В 1962 году Стивен окончил Оксфордский университет (степень B.A.), а в 1966 году в колледже Тринити-холл Кембриджского университета получил степень Ph.D. С 1965 Хокинг в Кембриджском университете. Работал исследователем в колледже Гонвил и Киз, в 1968—1972 в Институте теоретической астрономии, в 1972—1973 — в Институте астрономии, в 1973—1975 — на кафедре прикладной математики и теоретической физики, в 1975—1977 преподавал теорию гравитации, в 1977—1979 — профессор гравитационной физики, с 1979 — профессор математики. В 1974—1975 был стипендиатом в Калифорнийском технологическом институте.
В 1974 году Хокинг стал членом Лондонского королевского общества, в 1979 стал Лукасовским профессором Кембриджского университета. Эту должность он занимал до 2009 года.
В 1973 году посещал СССР, во время пребывания в Москве обсуждал проблемы чёрных дыр с советскими учёными Яковом Зельдовичем и Алексеем Старобинским.
Уже в начале 1960-х у Хокинга стали проявляться признаки бокового амиотрофического склероза, которые впоследствии привели к параличу. После диагностики заболевания в 1963 году врачи считали, что жить ему осталось лишь два с половиной года, однако болезнь прогрессировала не так быстро, и пользоваться коляской он начал только в конце 1960-х годов. В 1985 году Стивен Хокинг тяжело заболел, у него было воспаление лёгких. После серии операций ему была проведена трахеостомия, и Хокинг утратил способность говорить. Друзья подарили ему синтезатор речи, который был установлен на его кресле-коляске. Некоторую подвижность сохранял лишь указательный палец на правой руке Хокинга. Впоследствии подвижность осталась лишь в мимической мышце щеки, напротив которой закреплён датчик. С его помощью физик управляет компьютером, позволяющим ему общаться с окружающими.
Несмотря на тяжёлую болезнь, он ведёт активную жизнь. В 2007 году он совершил полёт в невесомости (на специальном самолёте), а на 2009 год был запланирован полёт в космос, который не состоялся. Сам про себя Хокинг говорит, что, будучи профессором математики, он никогда не получал никакого математического образования со времён средней школы. В первый год своего преподавания в Оксфорде Хокинг читал учебник, опережая собственных студентов на две недели.
Является атеистом.
Я думаю, каждый читающий эти строки знает о Хокинге достаточно, и поэтому не стану цитировать Википедию дальше.
В сообществе есть пост про Хокинга, который делали мы с Robot.
К сожалению, файлы с книгами удалены с обменников, но тем не менее...
Кстати, полезно цитировать Википедию. В топике по ссылке тоже текст из Википедии, и можно убедиться, что он претерпел за эти годы радикальные изменения.
И еще ссылки.
1. 10 интересных фактов из жизни Стивена Хокинга
2. Esquire Правила жизни. Стивен Хокинг
3. Стивен Хокинг hi-news.ru
4. Стивен Хокинг заявил о возможности выбраться из черной дыры Slon
5. Стивен Хокинг на vk.com Здесь есть и подборка его книг. Вот прямая ссылка: vk.com/topic-33047219_30455790
среда, 06 января 2016
что толку горевать?
читать дальше
безбожно долго размышлял над над таблицей истинности импликации
предположим A:= X>0 В:=X-1>0
эта эмпликация верна для х>1 на области действительных чисел, а для всей области верной не является и
выходит любое утвеждение может считаться верным пока не доказано обратное(презумпция невиновности)
также можно выделить утверждения которые являются обсюлютно верными на данной области (алгебраической структуре) A:= X>0 В:=X+1>0 (для действительных чисел)
и абсолютно ложными в том случае если нельзя выделить элемента где они выполняются
A:= X=0 В:=X-1>0
получается что ложные +верные в совокупности содержат в себе законы(аксиомы) алгебры(или даже в более широком смысле)
а безразличные (не абсолютные высказывания) формируют тело все возможных ситуаций ограниченых данными аксиомами
безбожно долго размышлял над над таблицей истинности импликации
предположим A:= X>0 В:=X-1>0
эта эмпликация верна для х>1 на области действительных чисел, а для всей области верной не является и
выходит любое утвеждение может считаться верным пока не доказано обратное(презумпция невиновности)
также можно выделить утверждения которые являются обсюлютно верными на данной области (алгебраической структуре) A:= X>0 В:=X+1>0 (для действительных чисел)
и абсолютно ложными в том случае если нельзя выделить элемента где они выполняются
A:= X=0 В:=X-1>0
получается что ложные +верные в совокупности содержат в себе законы(аксиомы) алгебры(или даже в более широком смысле)
а безразличные (не абсолютные высказывания) формируют тело все возможных ситуаций ограниченых данными аксиомами