Многоугольники

[wpoms.]

Множество n-угольников, лежащих в одной плоскости, назовем подходящим, если выполняются условия - все n-угольники множества - равные правильные многоугольники с числом вершин равным n; - если два n-угольника пересекаются, то они имеют ровно одну общую точку, являющуюся их общей вершиной; - все n-угольники множества пресекаются с одним и тем же количеством других n-угольников этого же множества. Пусть k - количество точек пересечения одного n-угольника из подходящего множества с другими n-угольниками из этого же множества, а m - количество n-угольников в подходящем множестве. 1. Пусть n=4, k=3. Найдите все возможные значения m. 2. Решите задачу в общем случае.

---

Вписанный четырёхугольник

[wpoms.]

Четырёхугольник `ABCD` вписан в окружность `omega_1` и середины всех сторон `ABCD` лежат на окружности `omega_2.` Докажите, что `/_ ABD + /_ BDC = 90^@.`

@темы: Планиметрия

---

Не простое

[wpoms.]

Дано простое число, десятичная запись которого содержит по меньшей мере 4 различные цифры. Докажите, что его цифры можно переставить в другом порядке так, чтобы полученное число не было простым.

@темы: Теория чисел

---

Предел

[AstroBoy96]

Здравствуйте. Как то не выходит предел. lim(x*(pi/4-arctg(x/(x+1)))) при x->inf. И если кто то знает как делать, то не подскажите где можно почитать про методы решения пределов.

@темы: Пределы

---

Натуральные числа. Прошу любить и жаловать

[wpoms.]

Дано, что $b$ и $c$ --- натуральные числа и что квадратное уравнение $x^2 - bx + c = 0$ имеет действительные корни $x_1$ и $x_2.$ Докажите, что a) $x_1^2 + x_2^2 + 2017;$ b) $x_1^3 + x_2^3$ --- натуральные числа.

@темы: Школьный курс алгебры и матанализа

---

Предел

[AstroBoy96]

Здравствуйте. Проблемка с пределом. Через замечательный предел не выходит, а чере просто математические преобразования прихожу к одному и тому же результату: к минус бесконечности. Подскажите, пожалуйста каким методом его брать)
`lim_{x->-oo}(4x-sqrt((16x^3-48x^2)/(x-5)))`

@темы: Пределы

---

Предел

[AstroBoy96]

Здравствуйте. Есть вот такой предел lim(x-ln(ch(x))) при x->+infinity. Не пойму, как тут все раскручивается. Не подскажете?)

@темы: Пределы

---

[MisteryS]

Решить задачу:

`10*u_t = u_{x x} + u_{yy} - 2*y;`
`u|_{x = 0} = 0, \ \ u_x|_{x = pi/2} = pi*y, \ \ u|_{y = 0} = 0, \ \ u|_{y = pi} = pi*x^2;`
`0 < x < pi/2`
`0 < y < pi`


Как я поняла, надо привести уравнение к однородному. Я ввела замену.... Но, наверно, краевые условия не должны получаться вот такими...ненулевыми?
Помогите, пожалуйста, решить это задание.

@темы: Уравнения мат. физики

---

тригонометрическое выражение.

[Alemand]

Можно ли вычислить значение ctg^2(36)*ctg^2(72) , без предварительного вычисления cos 18. (все в градусах)

---

Шарики

[wpoms.]

Каждый из шаров, лежащих в коробке, окрашен в один из $N$ цветов и на каждом шаре написано натуральное число не превосходящее $N.$ Известно, что каждый из $N$ цветов использован не менее одного раза и каждое натуральное число, не превосходящее $N,$ написано не менее одного раза. При каких значениях $N$ в коробке можно будет найти $N$ окрашенных в разные цвета шаров, на которых будут $N$ разных чисел?

@темы: Дискретная математика

---

Собственные числа

[MestnyBomzh]

Могли бы подтвердить/опровергнуть. Если надо найти собственные числа и собственные вектора для матрицы `A^(-2)`, то верно же я понимаю, что это будут `lambda^(-2)`? а собственные вектора останутся теми же? Это следует из разложения матрицы A в собственном базисе?

@темы: Линейная алгебра

---

Неравенство

[wpoms.]

Докажите, что `x^4 - x^2 - 3x + 4 > 0` выполняется для всех действительных `x.`

@темы: Школьный курс алгебры и матанализа, Рациональные уравнения (неравенства)

---

Планиметрия 8 кл ФМШ

[papan]

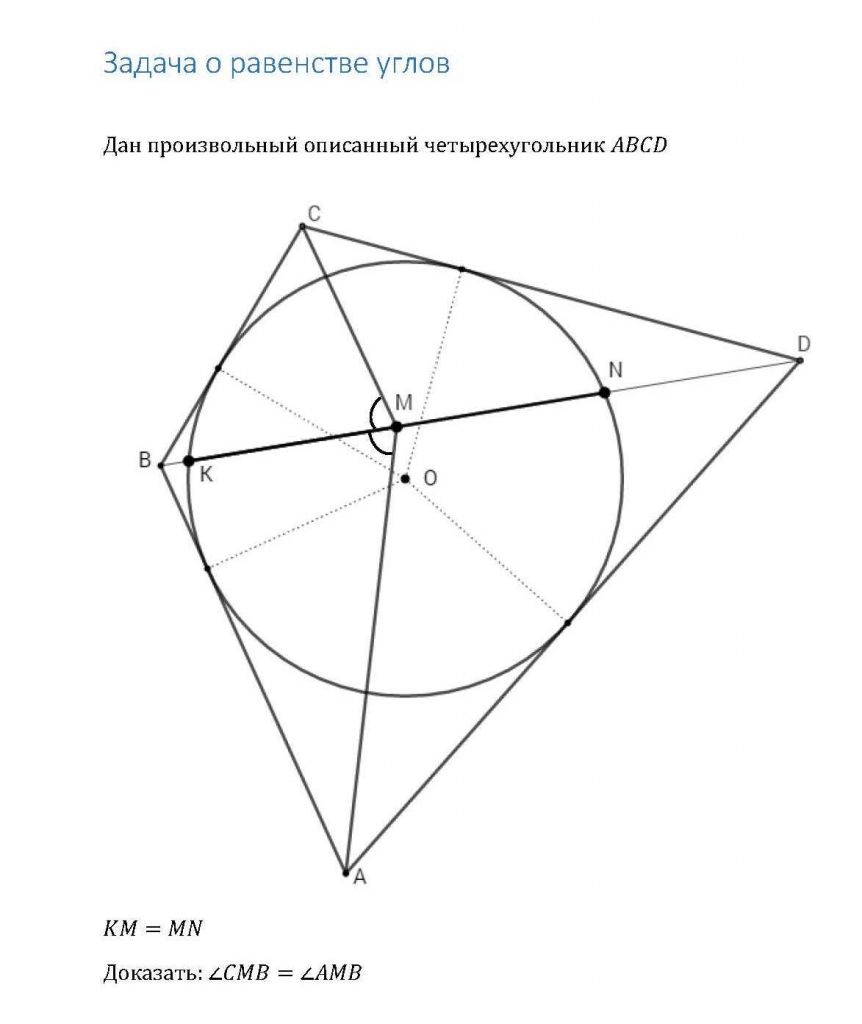
Помогите решить задачу элементарными геометрическими методами (без аналитической геометрии, без тригонометрии).

Условие задачи:
В четырехугольник ABCD вписана окружность. Хорда KN этой окружности лежит на диагонали BD четырехугольника.
Точка M - середина хорды KN. Из этой точки M к вершине A и к вершине C четырехугольника проведены отрезки MA и MC соответственно.
Доказать, что угол CMB равен углу AMB.

Что было сделано (конспективно):
Рассмотрены свойства описанного четырехугольника, вписанных углов,
а также теоремы, связанные с описанными четырехугольниками и вписанными окружностями:
1) Свойства окружности девяти точек (окружность Эйлера); прямая Эйлера.
2) Лемма о трезубце (теорема о трилистнике).
3) Теорема о бабочке.
4) Теорема Ньютона (о прямой, соединяющей середины диагоналей описанного четырехугольника)
и теорема Гаусса (о трех отрезках в произвольном четырехугольнике).

Удалось доказать следующее:
Пусть в рассмотренном выше описанном четырехугольнике сторона BC касается вписанной окружности в точке F, а сторона BA в точке P.
Пусть центр вписанной окружности точка O. Тогда нетрудно показать, что точки O, M, F, B, P лежат на одной окружности с диаметром OB.
Отсюда следует (это тоже несложно показать), что угол FMB равен углу PMB.

Дальше продвинуться не удалось...

@темы: Планиметрия

---

Профильный ЕГЭ по математике

[wpoms.]

Задачи, впечатления ...

Глава Рособрнадзора предложил ввести "месяц тишины" на период сдачи ЕГЭ
Подробнее на ТАСС: tass.ru/obschestvo/5241560

ЕГЭ по математике профильного уровня прошел в штатном режиме
obrnadzor.gov.ru/ru/press_center/news/index.php...

ПОМОЖЕМ РОСОБРНАДЗОРУ?
vk.com/boxdd?w=wall36288_11366

Пятый канал попросил прокомментировать эту утечку директора президентского физико-математического лицея № 239 Максима Пратусевича, который является членом экспертной комиссии ЕГЭ. Педагог назвал задания «неподлинными», отметив, что исходные материалы экзамена выглядят по-другому:
— То, что опубликовано у него (Дмитрия Гущина) на страничке, мало напоминает материалы ЕГЭ. Там оформление не такое. Исходное сырье выглядит не так. Задачи по формулировке тоже не такие, какие должны быть на экзамене. Я думаю, что это неподлинный вариант. Ему, значит, что-то пришло под видом вариантов ЕГЭ. Еще раз говорю, по виду не похожи.
Судя по всему, опубликованные в сети задания оказались фейком.
m.5-tv.ru/news/205678/

@темы: ЕГЭ

---

[Trotil]

Навеяно ночной задачкой:

найти предел последовательности средних арифметических и средних геометрических:

1) a, b, (a+b)/2, 1/2(b+(a+b)/2), ...
2) a, b, ab^(1/2), (b * ab^(1/2))^(0.5), ...
(решение одинаково, получается красивая простая формула)

3) найти предел последовательности смешанного среднеарифметических и геометрических.
a , b
(a+b)/2, (ab)^(1/2)
1/2 ((ab)^(1/2)+(a+b)/2), (1/2 (a+b)(ab)^(1/2))^(1/2)
...
эту я не решил пока.

@темы: Пределы, Головоломки и занимательные задачи

---

700 задач для 5-7 классов

[wpoms.]

Балаян Э.Н. 700 лучших олимпиадных и занимательных задач по математике / Э.Н. Балаян. — Изд. 4-е, испр. — Ростов н/Д: Феникс, 2015. — 217 с. : ил. — (Большая перемена)
В предлагаемом пособии рассмотрены различные методы и приемы решения олимпиадных задач разного уровня трудности для учащихся 5-6 классов.
Задачи, представленные в книге, посвящены таким, уже ставшим классическими, темам, как делимость и остатки, признаки делимости, инварианты, решение уравнений в целых числах, принцип Дирихле, задачи на проценты, числовые ребусы и т. п.
Ко всем задачам даны ответы и указания, а к наиболее трудным — решения. Большинство задач авторские, отмечены значком (А).
В заключительной части книги приводятся занимательные задачи творческого характера, вызывающие повышенный интерес не только у школьников, но и у взрослых читателей.
Ищем на gen.lib.rus.ec


Иванов С.В. (сост.) Математический кружок. Задачник первого-второго года обучения — СПб.: Санкт-Петербургский городской дворец творчества юных, 1993, 68 стр.
Предлагаемая брошюра продолжает серию учебно-методических изданий Аничкова лицея. Она содержит около 700 задач по всем основным разделам «олимпиадной» математики и предназначена для руководителей кружков, преподавателей, учащихся и всех любителей математической литературы. Уровень сложности задач примерно соответствует кружкам математики 6—9 классов, но многие из них будут интересны и старшеклассникам.
Практически каждый преподаватель кружка математики сталкивался с тем, что задачи, необходимые для занятий, разбросаны по многочисленным сборникам. С другой стороны, математические кружки в нашем городе существуют уже длительное время (с 1930-х годов), и с тех пор сложились определенные традиции преподавания и оригинальный математический фольклор, недостаточно отраженный в литературе. В своей работе жюри ленинградских олимпиад по математике также использовало, как правило, только новые, специально придуманные для олимпиады задачи. Поэтому книга, содержащая «историю кружка в задачах», представляется весьма полезной.
Предлагаемый сборник составлен по материалам кружка, занимавшегося в Ленинградском дворце пионеров в 1989—90 годах под руководством С. В. Иванова и С. К. Смирнова, которые, в свою очередь, опирались на своих предшественников и учителей.
Ищем на facebook.com

@темы: Методические материалы, Олимпиадные задачи, Литература

---

Сходимость последовательности

[MestnyBomzh]

Могли бы проверить моё решение. Решение пункта 1 мне кажется довольно громоздким

Последовательность `a_n` такова: что
1) все `a_n in (0;1)`
2) `a_{n+1} < (a_n+a_{n-1})/2`

Вопрос:
1) Сходится ли `a_n`?
2) Найти множество возможных пределов `a_n`

Моё решение:
1) От противного. Во-первых сразу отметим, что `a_n` не может расходиться к бесконечности, так как она ограничена. Тогда нам нужно только доказать то, что последовательность имеет один предел (то есть нельзя выделить подпоследовательность, которая бы сходилась к другому пределу). Предположим, можно выделить две подпоследовательности, сходящиеся к `a` и `b`. Не теряя общности `a<b`.
Тогда рассмотрим такие соседние члены `a_k` и `a_{k+1}`, что `a_k` лежит в бесконечно малой окрестности `b`, а `a_{k+1}` в бесконечно малой окрестности `a`. Тогда `a_{k+2} < (a+b+2 epsilon) / 2 = (a+b)/2 + epsilon`. Поскольку мы можем устремить `epsilon to 0`, то можно сделать вывод, что `a_{k+2}` лежит вне окрестности точки `b`. Тогда получили, что одновременно `a_{k+1}` и `a_{k+2}` лежат вне окрестности точки `b`. Последующие члены последовательности будут обязательно меньше, чем `max(a_{k+2}, a_{k+1})`, а значит никак не смогу попасть в окрестность `b`, значит в её окретсности не может лежать бесконечно много точек, а значит `a_n` не может иметь двух пределов.
2) Множество `(0;1)`. Построим последователньность, которая сходится к фиксированному числу `a`: `a_0 = a, a_1 = a+epsilon_1, a_2 = (a_0 + a_1)/2-epsilon_2 , a_3 = a, a_4 = (a_2 + a_3)/2-epsilon_3, a_5 = a,.`
Здесь все эпсилоны символизируют бесконечно малые величины

@темы: Математический анализ

---

Две случайных величины на отрезке

[MestnyBomzh]

Добрый день! У меня есть задача, могли бы проверить моё решение.
Задача:
На отрезке `[0;1]` в точках `x,y` независимо выбранных из равномерного распределения, находятся два детектора элементарных частиц. Детектор засекает частицу, если она пролетает на расстоянии не более `1/3` от него. Известно, что поля восприятия покрывают весь отрезок. С какой вероятностью `y >= 5/6` ?
Моё решение:
1) Я нарисовал в квадрате 1х1 множество точек, которые удовлетворяют условию "детекторы покрывают весь отрезок"

2) Далее надо найти условную вероятность: Р(y > 5/6 | покрыт весь отрезок). Я буду искать эту вероятность как отношение благоприятных исходов ко всевозможным. Я полагаю, что априори мы попали в закрашенную область, значит в знаменателе стоит площадь двух закрашенных треугольников: `S = 2 * 1/3 * 1/3 * 1/2`. Теперь числитель. Я взял пересечение y >= 5/6 и двух закрашенных треугольников, получается один треугольник, площадь которого равна `1/6*1/6*1/2`
3) Нахожу их отношение, получаю `0.125`

@темы: Теория вероятностей

---

Шифр

[wpoms.]

Все цифры в десятичной записи натурального числа заменили на буквы, одинаковые цифры заменили одинаковыми буквами, разные --- разными и получили `GANGA.` Известно, что при делении `GANGA` на 7 в остатке получается `A,` при делении `GANGA` на 11 в остатке получается `N,` при делении `GANGA` на 13 в остатке получается `G,` кроме того, `G > A > N.` Каким может быть оригинальное число?

@темы: Теория чисел

---

Уравнение с параметром

[asde21as1]

Найдите все значения a, при которых уравнение имеет единственное решение:

sqrt(x^4+(a-2)^4)=abs(x+a-2)+abs(x-a+2)



Заметим, что для f(x)=g(x)
f(x)=f(-x) и g(x)=g(-x)
Тогда единственное решение будет при x=0.

sqrt((a-2)^2)=abs(a-2)+abs(-(a-2))
(a-2)=t
abs(t^2)=abs(t)+abs(-t)
Рассмотрим два промежутка:
1. t>0 знаки ++- t^2+2t=0 t(t+2)=0 t1=0 t2=-2
2. t<0 знаки +-+ t^2-2t=0 t(t-2)=0 t1=0 t2=2

Тогда (a-2)=0
(a-2)=2
(a-2)=-2

a=0, a=2, a=4

Верно?

@темы: Задачи с параметром, ЕГЭ