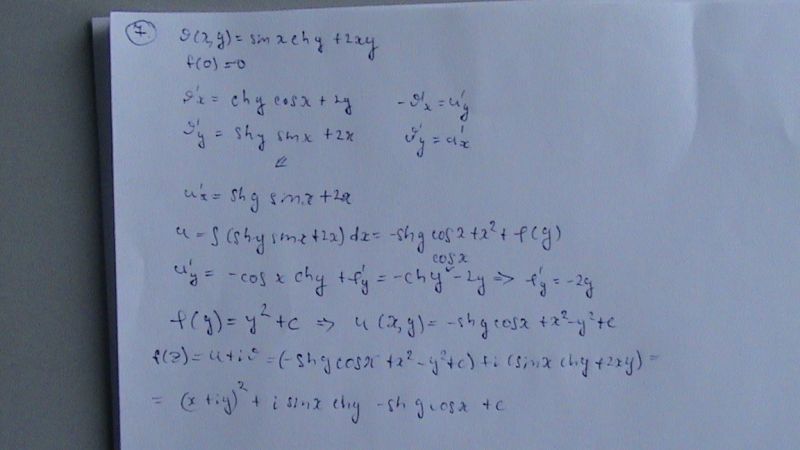1)Точки лежат на прямой AB.Определить координаты точек F,L,T при условии,что координат Х точки F равна 30мм, Y точки L равна 30мм,а Z точки T равна 10 мм.
прямая аб получается не параллельно оси Ох?
2)Определить лежат ли точки P,S,Q на прямой CD. Известно,что их фронтальные проекции принадлежат фронтальной проекции прямой ,а горизонтальные определяются координатами (30;40) , (10;50) , (20;35)
построила горизонтальные проекции точек,а как двигаться дальше?
3)Отрезок прямой AB разделить в соотношении 1:2:3 .Записать координаты точек,делящих отрезок.
как лучше расположить прямую?
темы саме первые: прямая, нахождение длины отрезка, угол наклона прямой к плоскостям проекций, след прямой, параллельные ,скрещивающиеся прямые и т.д.
Может быть, кто-нибудь сталкивался с этим. Лучше,конечно, видео уроки. заранее спасибо.
X = {n/(2*n+3)} , n∈N
Найти sup X, inf X, max X, min X.
Решал так:
n/(2*n+3)<=1( так как числитель меньше знаменателя, то дробь будет меньше единицы)
Разложил в другом варианте дробь:
n/(2*n+3)=1/2 - 3/(4*n+6)
В графическом варианте, 1/2 - горизонтальная ассимптота, -3/2 - вертикальная. max X и min X не существует, а sup X= -3/2, inf X = 1/2 ? Если не правильно, объясните, пожалуйста, как решить.
Для всякого многочлена `f \in P[z]` степени `n >= 1` существует хотя бы одно поле разложения - такое минимальное расширение `F` поля `P`, в котором содержатся все корни многочлена `f`.
-линейная алгебра
-первый курс
-крайний срок -вечер завтра
-4х1+3х2-3х3=3
-х1-5х2+6х3=5
3х1+4х2+х3=m
я так понимаю, что определения несовместности системы, в системе где-то должна получится такая картина 0 0 0=m плюс или минус что-то
у меня такая картина не получается.
может решаю что-то не так.
первым шагом выбирала разрешающий элемент -1.
второй шаг уже не получается(
Проблема в том, что я возможно не смогу описать все возможные комбинации делителей. Вот так я начала записывать:
1.) 5000 = 13 х 3 х 2 х 2 х 2 х 2 х 2 х 2 х 2
Здесь выходит n = 2α1 • 3α2 • 5α3 • 7a4 • 11a5 • 13a7 • 17a8 • 19a9 • 23a10
при этом α1+1=13, α2+1=3, α3+1=2, a4+1=2, a5+1 = 2 и все последующие равны 2.
n = 4096*9*5*7*11*13*17*19*23 = (ну в общем большое)
2.) 5000 = 128 х 13 х 3
Здесь выходит n = 2α1 • 3α2 • 5α3
при этом α1+1=128, α2+1=13, α3+1=3
Это чересчур большое, больше первого, значит не подходит
3.) 5000 = 13 х 12 х 8 х 4
Здесь выходит n = 2α1 • 3α2 • 5α3 • 7a4
при этом α1+1=13, α2+1=12, α3+1=8, a4+1=4
n=4096*177147*78125*343
Это меньше второго, но больше первого, так что не подходит
Ну и тут можно ещё перебирать..
Только вот я могу какой-то вариант перебора не заметить и нет ли ещё какого-то способа найти это число? Чтобы была 100% уверенность, что это число наименьшее из возможных с 5000 делителей?
1) `sqrt(13-12*sinx) + sqrt(7-4*sqrt(3)*sinx)=2*sqrt(3)`
Решить уравнение при `0<x<90` .
Пробывал возводить в степени, делать замены, вплоть до двойных, к рациональному виду уравнения не дошел .
Что можно предпринять, что б решить данное уравнение?
2) Далее есть задание, найти такие числа a и b, что
`sqrt(0,a a a)=0,b b b b`
методом тыка, другого не знаю в данном случае, выяснил что
`sqrt(0,444444...)=0,666666....`
`3*sqrt(3) + x^3 + 3x^2*sqrt(3) + 9x = sqrt(3)*(3+3*x^2)+x^3+9x`. тут все понятно, но дальше происходит что-то странное. появляется система уравнений, состоящая из: `3x^2+3=6` и `x^3+9x=10`. (в скобках у меня помечено, что `x=1` понятия не имею, почему). а дальше самое первое выражение становится равным `10+6*sqrt(3)`.
возможно, я ошиблась при записи, под катам фото решения
раньше этот пример я хоть с натяжкой, но понимала, но теперь совершенно в растерянности, что значат мои же записи. насколько я помню, так как в примере встречалось `x^3`, можно было сделать вывод, что должна будет использоваться формула сокращенного выражения с кубами. скорее всего, куб суммы. а далее мы представляли выражение в виде формулы и получали результат. Но как это произошло, я не понимаю, поэтому, хотела бы попросить объяснить данный метод, желательно простыми словами. так же хотелось бы узнать, как можно распознать выражение, где нужно применить этот метод и в какой книге можно порешать простые примеры на него. Заранее огромное спасибо.
 |
Емельянов В.М., Рыбакина Е.А. Уравнения математической физики. Практикум по решению задач. Лань, 2008. 213 стр. |
 |
Пиаджио Г. Интегрирование дифференциальных уравнений. ГИТТЛ, 1933. 350 стр. |
На компьютере уже это сделал, но как это осуществить в "боевых" условиях? Есть ли какой-нибудь метод?
Заранее спасибо!
 |
Демидович Б.П. Задачи и упражнения по математическому анализу для ВТУЗов. — М.: ООО "Астрель", 2004, 495 с. |
Содержание
Примечание
Книга добавлена на полку Решебники по высшей математике (руководства по решению задач)
Администрация
`|vec(a)|=1`
`|vec(b)|=2`
`vec(a)` и `vec(b)=pi/3`
`(vec(a)+alpha*vec(b))_|_(vec(a)-vec(b))`?
Так как векторы перпендикулярны, то их скалярное произведение равно 0.
`(vec(a)+alpha*vec(b))*(vec(a)-vec(b))=0`
`(vec(a)^2-vec(a)*vec(b)+alpha*vec(b)*vec(a)-alpha*vec(b)^2)=0`
как это посчитать?
подскажите как решать пожалуйста
и не знаете ли вы как в вольфраме составлять уравнение эйлера-пуассона для вариационго исчисления?
7. Найти, если возможно, аналитическую функцию `f(z)=u(x,y)+iv(x,y)`, для которой `v(x,y)=sinx*chy+2xy`
Решение
Я вот не могу сообразить, как преобразовать последнюю строчку. Подскажите пожалуйста.
С чего начать упрощать?
затрудняюсь выбрать @тему
 |
Александрова Л.А. Алгебра. 11 класс. Самостоятельные работы |