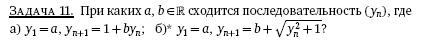Нужна помощь по аналитической геометрии и векторам

[chrom-look]

Доброго времени суток
Имеется 4 задачи на руках, решить никак не удается. Прошу помощи) Надо бы до завтрашнего дня их сделать.

1) Найти при каком t векторы p=a+tb и q=a-tb будут взаимно перпендикулярны, если a=6i+2j-3k, b=3i-4k.
Ответ к ней вроде бы 7/5 и -7/5...

2) Составить уравнение плоскости, проходящей через начало координат и перпендикулярной к двум плоскостям: 2x-y+5z+3=0 и x+3y-z-7=0

3) Найти уравнения прямых, проходящих через точку М(-1;2) под углом 45 гр. к прямой x-2y+3=0.
Эту вроде бы почти решил, но попал в тупик с последним действием, а именно: я нашел b1 и b2 которые равны 5 и 1, но как записать два уравнения с помощью них я не пойму.

4) Даны точки пересечения прямой с двумя координатными плоскостями (x1,y1,0) и (x2,0,z2). Вычислить координаты точки пересечения этой же прямой с третьей координатной плоскостью.

Буду примного благодарен если поможете с решением
P.S. Зарегистрировался только сегодня, так как не нашел для себя ответов на эти задачи в вашем сообществе и интернете.. Раньше активно посещал страничку

@темы: Аналитическая геометрия, Векторная алгебра

---

Помогите пожалуйста решить предел

[Та Самая)]

Не знаю как раскрыть неопределенность

(вопрос решен)

@темы: Пределы

---

Помогите бедной заочнице...

[001katrin001]

Вычислить неопределённый интеграл. Не могу подобрать формулу, или перед этим нужно сделать какие-то преобразования?

@темы: Интегралы

---

[Linker1989]

Помогите пожалуйста найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей А

Не могу найти собственные значения делал как тут , но у меня в первой строчке нули идут так что не знаю как делать! webmath.exponenta.ru/s/pyartli1/node80.htm

@темы: Линейные преобразования

---

решить систему матриц методом Жордана

[муляж сердца.]

х1+2х2+4х3-3х4=0
3х1+5х2+6х3-4х4=0
4х1+5х2-2х3+3х4=0
3х1+8х2+24х3-19х4=0

(икс не в степени.это нижний индекс как бы)
вроде решаю нормально но получается строчка из нулей или в одном столбике остается 2 чила.перерешивала уже много раз но каждый раз что то не так получается
помогите пожалуйста,и если можно поместите конкретное решение.буду очень признательна.

@темы: Системы линейных уравнений

---

Найти предел

[[email protected]]

lim x*x/((1+3*x)^(1/3)-(1+x))
x->0
вообще не знаю что с тим делать.пробовала уже и выносить х,и домножать.помогите,пожалуйста
(разобрано)

@темы: Пределы

---

Помогите пожалуйста решить задачу) Дайте направление, в котором шагать!

[Та Самая)]

Две стороны треугольника заданы уравнениями
5x-2y-8=0
3x-2y-8=0
а середина третьей совпадает с началом координат. Составить уравнение этой стороны.
(сделано)

@темы: Аналитическая геометрия

---

Предел последовательности

[AC99]

Помогите решить.

Доказать, что lim Xn = a при n стремится к бесконечности, определив для каждого E>0 число N=N(E) такое, что
|Xn-a|< E для всех n > N(E). Определить N(E) при E = 0.1 , 0.01 , 0.001


Xn = (n-1)/(1-2n) , a = - 1/2

Как решал: |(n-1)/(1-2n) + 1/2|< E

|(-1)/ (2(1-2n))|< E
1/ (2(1-2n))< E
1/ (2E)< (1-2n)
n < 2 - 1/(4E)
А должно же быть n > N(E) .
Что делать дальше или где ошибка?
(сделано)

@темы: Пределы

---

Сумма цифр квадрата целого числа

[Fidd]

Пожалуйста, помогите. Может ли квадрат целого числа иметь сумму цифр, равную 6030? а 6034?
(дано указание)

@темы: Теория чисел

---

Геометрия. Векторы.

[separatrix*]

Пожалуйста, помогите.

Геометрия за 8-9 класс. Тема: векторы. Контрольные задания. Крайний срок: до сегодняшнего вечера.

Задание.
На стороне CD квадрата ABCD лежит точка P так, что CP=PD, O - точка пересечения диагоналей. Выразите векторы BO, BP, PA через векторы x = BA и y = BC ( над всеми векторами стрелочки)
Рисунка нет, в принципе, он понятен.

Не понимаю, получаются ли векторы AC и AP, BP и BD параллельными? Или вообще надо мыслить в другом направлении?
Кажется, ВО - это 1/2 АВ, т.к. в квадрате все стороны равны.
А вот с двумы остальными векторами запуталась...Помогите, пожалуйста. Думаю, задания достаточно легкие, но с геометрией у меня не очень.

@темы: Планиметрия

---

Помогите плз с оператором

[Linago]

Есть оператор и его матрица. Из заданий расчетки не понимаю как найти базис спектра, базис подпространства оператора и его канонический базис.
И еще нужно сделать какуюто проверку C^-1AC = diag(L1,L2,L3) L-лямбда

@темы: Линейная алгебра, Линейные преобразования

---

Можно ли так решать?

[~Charmander~]

Задание: Найдите сумму корней уравнения cos^2(x)-2cos(x)=3 на промежутке (-5П;8П)

Как я решал: cos(x)=t => t^2-2t-3=0
t(1)=3 t(2)=-1

cos(x)=-1
x=П+2ПK, K Z
-5П < x < 8П
-5П < П+2ПK < 8П
Так вот дальше у меня почему-то не сходится ответ

@темы: Тригонометрия

---

Подскажите и проверьте пожалуйста

[Nurmi]

Исследовать методами дифференциального исчисления функцию f(x) и, построить ее график.
f(x)=x^3-lnx^3
Область определения функции от 0 до бесконечности.
Пересечение с осью oy нет.
Ось oy является вертикальной асимптотой графика.
Наклоных асимптот нет.
Точка возможного экстремума х=1
Промежутки монотонности функции (0;1)U(1; бесконечность)
В точке 0 f'(x)-не существует, на отрезке (0;1) "-", в точке 1=0, на отрезке (1;бесконечность) "+"
В точке 0 f(x)-не существует, на отрезке (0;1) "\", в точке 1=0, на отрезке (1;бесконечность) "/"
Правильно?
И еще вопрос надо ли находить критические точки, потому что при их нахождении получается бессмыслица, они у меня получается меньше 0, хотя график я могу построить и без них. График получается похожий на параболу с вершиной в точке (1,1) где левая часть стремится к оси у, а правая часть подобна параболе.
(разобрано)

@темы: Исследование функций

---

С4 вариант 4 Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010

[Robot]

Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. АЛ. Семенова, И.В. Яшенко. — М.: ACT: Астрель, 2010.—93,131 с. — (Федеральный институт педагогических измерений).
С4 вариант 4
SPI.С4.4. В параллелограмме ABCD известны стороны АВ = а, ВС = b и ∠BAD=α. Найдите расстояние между центрами окружностей, описанных около треугольников BCD и DAB.
В данной задаче нам поможет разобранная ранее задача варианта 2 SPI.С4.2.
По свойству параллелограмма треугольники BCD и DAB равны, а значит, равны и радиусы R окружностей, описанных около них. Обозначим диагональ параллелограмма BD через 2d. Одновременно BD будет являться общей хордой пересекающихся окружностей. По теореме косинусов

По теореме синусов радиус окружностей, описанных около рассматриваемых треугольников

Заметим, что каким бы ни был угол α - тупым или острым - центры этих окружностей О₁ и О₂ либо оба будут лежать вне треугольников, либо оба внутри, а потому они обязательно будут лежать по разные стороны от их общей хорды - диагонали BD
Следовательно, в данном случае мы можем воспользоваться первой из формул, рассмотренных в предыдущей задаче SPI.С4.2.. С учетом того, что радиусы окружностей равны

Подставляя выражение для 2d, имеем

Ой, да, чуть не забыла чертеж. В принципе он нам в данном случае не понадобился, поскольку мы ссылались на рассмотренную выше задачу, тем не менее

Ссылки на разбор и решения остальных задач пособия Самое полное издание типовых вариантов реальных заданий ЕГЭ-2010

@темы: Планиметрия, ЕГЭ

---

С4 вариант 3 Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010

[Robot]

Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. АЛ. Семенова, И.В. Яшенко. — М.: ACT: Астрель, 2010.—93,131 с. — (Федеральный институт педагогических измерений).
С4 вариант 3
Дана окружность и точка М. Точки А и В лежат на окружности, причем А — ближайшая к М точка окружности, а В — наиболее удаленная от М точка окружности. Найдите радиус окружности, если МА = а и MB = b.

Совсем простая задача, если не доказывать тот факт, что наиболее близкая к М и наиболее удаленная от нее точки лежат на прямой, проходящей через М и центр окружности.
Возникает вопрос - требует ли это доказательства и если да, то как оно там в школе доказывается.

В остальном все видно на картинке. В зависимости от положения точки М (вне круга, ограниченного окружностью или внутри него) имеем два случая: диаметр равен b-a или b+a, соответственно радиус равен (b-a)/2 или (b+a)/2

Ссылки на разбор и решения остальных задач пособия Самое полное издание типовых вариантов реальных заданий ЕГЭ-2010

@темы: Планиметрия, ЕГЭ

---

С4 Вариант 2 Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010

[Robot]

Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. АЛ. Семенова, И.В. Яшенко. — М.: ACT: Астрель, 2010.—93,131 с. — (Федеральный институт педагогических измерений).
С4 вариант 2
SPI.С4.2. Окружности радиусов 10 и 17 пересекаются в точках A и В, Найдите расстояние между центрами окружностей, если АВ = 16.
Задача достаточно простая, опирается на известный из школьного курса планиметрии факт: линия центров пересекающихся окружностей перпендикулярна их общей хорде и делит ее пополам (Вопрос: нужно ли это доказывать на ЕГЭ?)
Два случая, возникающих в задаче, связаны с тем, лежат ли центры окружностей по разные стороны от их общей хорды или же по одну.
1 случай

Центры окружностей лежат по разные стороны от хорды АВ, О₁ - центр меньшей, О₂ - центр большей окружности. Обозначим через С точку пересечения О₁О₂ с АВ. Исходя из вышенаписанного АС=СВ=8.
В этом случае О₁О₂=О₁С+СО₂, где каждое из слагаемых находится по теореме Пифагора из соответствующих треугольников. В данном случае О₁С=6, О₂С= 15, откуда расстояние между центрами равно 21.
Второй случай

Центры окружностей лежат по одну сторону от хорды АВ. Длины отрезков О₁С и СО₂ те же, однако О₁О₂=О₂С-О₁С=15-6=9
P.S. Приступила к задаче варианта 4. наверное, понадобится обобщение этой задачи.
Окружности радиусов R₁ и R₂ (R₂ ≥R₁) пересекаются в точках A и В, АВ = 2d, тогда расстояние между центрами окружностей О₁ и О₂

Ссылки на разбор и решения остальных задач пособия Самое полное издание типовых вариантов реальных заданий ЕГЭ-2010

@темы: Планиметрия, ЕГЭ

---

С4 Вариант 6 Самое полное издание типовых вариантов реальных заданий ЕГЭ

[Robot]

Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010 (Федеральный институт педагогических измерений).
С4 Вариант 6

SPI.С4.6. Медиана ВМ треугольника ABC равна его высоте АН. Найдите угол МВС.

Обозначим искомый угол α. Для его нахождения воспользуемся методом площадей. Учтем, что медиана ВМ треугольника АВС разбивает его на два равновеликих треугольника, то есть S_ΔАВС=2S_ΔВМС=ВМ*ВС*sinα. С другой стороны, S_ΔАВС=(1/2)*ВС*АН. Приравнивая площади и учитывая, что АН=ВМ, получаем, что sinα=1/2, откуда α=30° или α=150°. Рисунки , соответствующие этим случаям, выложены ниже.

Вопрос: достаточно ли этого? Может ли такой рисунок считаться доказательством возможности второго случая?

Ссылки на разбор и решения остальных задач пособия Самое полное издание типовых вариантов реальных заданий ЕГЭ-2010

@темы: Планиметрия, ЕГЭ

---

С4 Вариант 5 Самое полное издание типовых вариантов

[Robot]

По просьбе  krasn, высказанной как у нас, так и на форуме альбеги, начинаю выкладывать задачи С4 из сборника «Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010 (Федеральный институт педагогических измерений)».
Просьба внимательно проверять, критиковать и и обогащать другими способами решения.
Вариант 5 С4
SPI.С4.5.
Дан прямоугольный треугольник ABC с прямым углом при вершине В и углом α при вершине А, Точка D — середина гипотенузы. Точка С₁ симметрична точке С относительно прямой BD. Найдите угол АС₁В.
Положение точки С₁ зависит от значения угла А.

Рассмотрим случай, когда α < 45°.

Рисунок ( α < 45)

По свойству медианы, проведенной к гипотенузе прямоугольного треугольника AD=BD=DC, а из симметричноcти точек С и С₁ следует ВС=ВС₁ и DC=DС₁, а отсюда равны равнобедренные треугольники BDC и BDС₁. Так как ∠ACB=90°-α, то ∠ВС₁D=90°-α. Поскольку треугольник BDC - равнобедренный и углы при основании равны 90°-α, то ∠BDC= ∠BDC₁=2α, откуда ∠С₁DB= ∠BDC+ ∠BDC₁=4α. Так как равнобедренным является и треугольник ADС₁, а внешний угол треугольника равен сумме внутренних, не смежных с ним, то ∠DC₁A=2α.
Отсюда искомый угол АС₁В=90°+α
Рассмотрим случай, когда α > 45°.

Рисунок (α > 45°)

Аналогично предыдущему пункту AD=BD=DC, а из симметричноcти точек С и С₁ следует и равенство DC=DС₁, откуда AD=DC₁=BD. Тогда ∠ADB=∠1=180°-2α, равный ему вертикальный угол СDE, а также угол EDC₁равны 180-2α, а тогда ∠СDС₁=360°-4α. Используя дважды теорему о внешнем угле треугольника, получаем, что DC₁A=180°-2α, а ∠BC₁D=90°-α, откуда искомый угол АС₁В=90°-α.
Если α=45°, то точка С1 совпадает с точкой А, откуда АС₁В=?

Примечания: 1) кажется все очень громоздким
2) вроде как прослеживается параллельность, м.б. она позволила бы получить результат легче
Какие у кого способы?

Я думаю, что самый здесь рациональный способ Гостя. И мой способ весь надо зачеркнуть и стыдливо спрятать куда-нибудь в темное место! Гость, спасибо!
Способ Гостя.
Так как DA=DC1=DB=DC, то точки A, B, C и С1 лежат на одной окружности
После доказательства того, что С1 принадлежит описанной окружности, можно было бы перейти к вписанным в нее углам.
В первом случае получаем AC1B + ACB = 180. Во втором, AC1B = ACB.
Чертеж для первого случая.

Ссылки на разбор и решения остальных задач пособия Самое полное издание типовых вариантов реальных заданий ЕГЭ-2010

@темы: Планиметрия, ЕГЭ

---

Помогите решить

[dirkul]

Помогите решить две задачки.
Нужно написать уравнение плоскости Р, проходящей через точку А(2,-1,3) и прямую А1В1, где координаты точки А1(2,0,1).
Написать уравнение плоскости, проходящей через точки А(2,-1,3) и С1, перпендикулярно плоскости 3x+3z-15=0.
Заранее спасибо

@темы: Аналитическая геометрия

---

Примечание Robot: Поднимаю

[Garryncha]

Подскажите, пожалуйста, как решить задачу.


Нужно решить пункт б), если есть желание, можно проверить ответ а):
1) a = 1/(1-b), b != 1.
2) a != 1/(1-b), |b| < 1. В обоих случаях lim y_n = 1 / (1-b).

В пункте b) у меня были такие соображения.
Если перенести b в правую часть, возвести в квадрат и раскрыть скобки, а потом перейти к пределу (переход законен в силу предположения о сходимости последовательности и теорем о пределах), то получится (если предел последовательности z):
z^2 - 2 * b * z + b^2 = z^2 + 1, отсюда z = (b^2 - 1) / (2 * b).
Т.к. все члены последовательности, кроме, может быть, первого, > b, то и z > b.
(b^2 - 1) / (2 * b) > b => b < 0. Получили первое условие на параметры.
А что делать дальше?

(Примечание Robot: Поднимаю. Большая просьба помочь хорошему человеку, который сам уже многим помог в сообществе)

запись создана: 30.10.2009 в 15:43

@темы: Математический анализ, Пределы, Школьный курс алгебры и матанализа