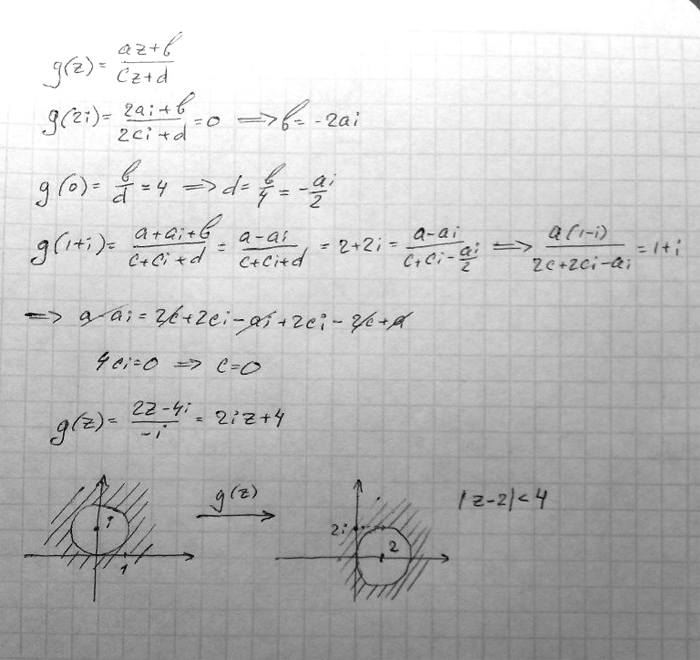вторник, 03 мая 2016
В треугольной пирамиде с равными боковыми ребрами известны длины сторон основания 6, 8, 10 и длина высота 1. Найдите радиус описанного шара.
понедельник, 02 мая 2016
Step by step ...
Множество A состоит из натуральных чисел, причем 1) 1 принадлежит A, 2) если a принадлежит A, то и 2a + 1 принадлежит A; 3) если 3a + 1 принадлежит A, то a принадлежит A. Верно ли, что множеству A принадлежит
а) число 42;
б) число 8;
в) произвольное натуральное число?
% Р.П. Ушаков
а) число 42;
б) число 8;
в) произвольное натуральное число?
% Р.П. Ушаков
пятница, 29 апреля 2016
такое вот задание: найдите собственное расширение поля Z(3)
помогите пожалуйста
помогите пожалуйста
четверг, 28 апреля 2016
На плечах гигантов, на спинах электронов
Декларации депутатов и чиновников.
Шизофренические числа Математические свойства думских и правительственных зарплат

В апреле президент, министры, губернаторы и депутаты опубликовали декларации о своих доходах за 2015 год. Из них мы узнали, например, что доходы Владимира Путина за этот период выросли на миллион рублей, тогда как депутат-единорос Леонид Симановский заработал почти миллиард. Впрочем, все эти данные — довольно скучные; мы же решили взглянуть на них (только не спрашивайте, зачем) с математической точки зрения: поискали простые числа, покопались в миллионах знаков числа пи и присмотрелись к «шизофреническому числу».
Для тех, кого мало интересуют зарплаты чиновников, надеюсь найдется много интересного из "занимательной теории чисел" ))
Про шизофренические числа я не знала
Шизофренические числа Математические свойства думских и правительственных зарплат

В апреле президент, министры, губернаторы и депутаты опубликовали декларации о своих доходах за 2015 год. Из них мы узнали, например, что доходы Владимира Путина за этот период выросли на миллион рублей, тогда как депутат-единорос Леонид Симановский заработал почти миллиард. Впрочем, все эти данные — довольно скучные; мы же решили взглянуть на них (только не спрашивайте, зачем) с математической точки зрения: поискали простые числа, покопались в миллионах знаков числа пи и присмотрелись к «шизофреническому числу».
Для тех, кого мало интересуют зарплаты чиновников, надеюсь найдется много интересного из "занимательной теории чисел" ))
Про шизофренические числа я не знала

среда, 27 апреля 2016
Step by step ...
Математика в школе, № 31,2
5453.
У царя Гиерона есть 11 слитков, неразличимых на вид; царь знает, что их веса (в некотором порядке) равны 1, 2, ..., 11 мин. Ещё у него есть мешок, который порвётся, если в него положить больше 11 мин. Архимед узнал веса всех слитков и хочет доказать Гиерону, что первый слиток весит 1 мину. За один шаг он может загрузить несколько слитков в мешок и продемонстрировать Гиерону, что мешок не порвался (рвать мешок нельзя!). За какое наименьшее число загрузок мешка Архимед может добиться требуемого?
%И.И. Богданов (Москва), К.А. Кноп (С.-Петербург)
5454.
Непустое множество `A \subseteq R` назовём заполненным, если для любых `x, y \in R` (не обязательно различных и не обязательно лежащих в `A`) таких, что `(x+y) \in A`, число `xy` также лежит в `A`. Найдите все заполненные множества.
%Н.X. Агаханов (Москва)
5455.
Каким может быть число `a>0`, если для некоторой строго убывающей функции `f: (0, +\infty) \to (0, +\infty)` и любого `x \in (0, +\infty)` выполняется неравенство `f(x) >= af(x + f(x))`?
%Ш.Н. Исмаилов (Ташкент, Узбекистан)
5456.
Каждая прямая, проходящая через пару смежных вершин `n`-угольника, содержит ещё хотя бы одну из его вершин. Каким наименьшим может быть число `n`?
%Е.В. Бакаев (Москва)
5457.
Докажите, что неравенство
`{n sqrt2} [n sqrt2] < 1/2`
имеет бесконечное множество натуральных решений (`{a}` и `[a]` -- дробная и целая части числа `a` соответственно).
%М. А. Муртузалиев, Ш.Г. Гамидов (Махачкала)
---------------------------------------
1 vk.com/club1126038
2 В журнале не указано, что некоторые задачи предлагались на областном этапе российской олимпиады.
5453.
У царя Гиерона есть 11 слитков, неразличимых на вид; царь знает, что их веса (в некотором порядке) равны 1, 2, ..., 11 мин. Ещё у него есть мешок, который порвётся, если в него положить больше 11 мин. Архимед узнал веса всех слитков и хочет доказать Гиерону, что первый слиток весит 1 мину. За один шаг он может загрузить несколько слитков в мешок и продемонстрировать Гиерону, что мешок не порвался (рвать мешок нельзя!). За какое наименьшее число загрузок мешка Архимед может добиться требуемого?
%И.И. Богданов (Москва), К.А. Кноп (С.-Петербург)
5454.
Непустое множество `A \subseteq R` назовём заполненным, если для любых `x, y \in R` (не обязательно различных и не обязательно лежащих в `A`) таких, что `(x+y) \in A`, число `xy` также лежит в `A`. Найдите все заполненные множества.
%Н.X. Агаханов (Москва)
5455.
Каким может быть число `a>0`, если для некоторой строго убывающей функции `f: (0, +\infty) \to (0, +\infty)` и любого `x \in (0, +\infty)` выполняется неравенство `f(x) >= af(x + f(x))`?
%Ш.Н. Исмаилов (Ташкент, Узбекистан)
5456.
Каждая прямая, проходящая через пару смежных вершин `n`-угольника, содержит ещё хотя бы одну из его вершин. Каким наименьшим может быть число `n`?
%Е.В. Бакаев (Москва)
5457.
Докажите, что неравенство
`{n sqrt2} [n sqrt2] < 1/2`
имеет бесконечное множество натуральных решений (`{a}` и `[a]` -- дробная и целая части числа `a` соответственно).
%М. А. Муртузалиев, Ш.Г. Гамидов (Махачкала)
---------------------------------------
1 vk.com/club1126038
2 В журнале не указано, что некоторые задачи предлагались на областном этапе российской олимпиады.
понедельник, 25 апреля 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
двойной интеграл (x+y+s)dS, где S-поверхность x^2+y^2+z^2=a^2, z=>0
пытался перейти в сферические координаты, но ответ не сходится, расставил пределы от 0 до 2pi и от 0 до pi/2
dS=a^2sindфи
пытался перейти в сферические координаты, но ответ не сходится, расставил пределы от 0 до 2pi и от 0 до pi/2
dS=a^2sindфи
здравствуйте уважаемое сообщество
учусь на втором курсе прикладной математики Каунасского Технологического Университета.
проблема такая - делаем презентацию на английском языке по предметной области математики на 6 минут со сладами.
я решил сделать по случайным числам и генератору случайных чисел отсюда
https://en.wikipedia.org/wiki/Randomness
и отсюда
https://en.wikipedia.org/wiki/Pseudorandom_number_generator
Помогите пожалуйста как озвучить формулы и математические выражения на английском языке
читать дальше
простите пожалуйста, если не совсем по теме
thanks in advance
учусь на втором курсе прикладной математики Каунасского Технологического Университета.
проблема такая - делаем презентацию на английском языке по предметной области математики на 6 минут со сладами.
я решил сделать по случайным числам и генератору случайных чисел отсюда
https://en.wikipedia.org/wiki/Randomness
и отсюда
https://en.wikipedia.org/wiki/Pseudorandom_number_generator
Помогите пожалуйста как озвучить формулы и математические выражения на английском языке
читать дальше
простите пожалуйста, если не совсем по теме
thanks in advance
воскресенье, 24 апреля 2016
Построить квадратуру Гаусса с двумя узлами `I(f) = int_0^pi (sin(x)*f(x))dx = c_1*f(x_1)+c_2*f(x_2)`
читать дальше
читать дальше
Найти площадь фигуры, ограниченной гиперболой `x^2/a^2-y^2/b^2=1` и прямой `x=2a`.
`f(x)=bsqrt((x/a)^2-1)`
`bint_{a}^{2a} sqrt((x/a)^2-1)dx=bint_{a}^{2a} sqrt(-(1-(x/a)^2))dx=[(x/a=sint), (x=asint), (dx=acostdt)]=abint_{pi/2)^{arcsin2} sqrt(-(1-sin^2t))dt`... но тогда подкоренное выражение отрицательно на указанном интервале...как быть?
`f(x)=bsqrt((x/a)^2-1)`
`bint_{a}^{2a} sqrt((x/a)^2-1)dx=bint_{a}^{2a} sqrt(-(1-(x/a)^2))dx=[(x/a=sint), (x=asint), (dx=acostdt)]=abint_{pi/2)^{arcsin2} sqrt(-(1-sin^2t))dt`... но тогда подкоренное выражение отрицательно на указанном интервале...как быть?
пятница, 22 апреля 2016
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Есть задача: найти какую-нибудь дробно-линейную функцию g(z), удовлетворяющую условиям g(0)=4; g(1+i)=2i+2; g(2i)=0. И еще найти образ круга |z-i|<1 под действием функции g(z).
Я задачу решила, но мне было сказано, что есть ошибки.
читать дальше
Я задачу решила, но мне было сказано, что есть ошибки.
читать дальше
четверг, 21 апреля 2016
Доказать тождество: в числителе 2 sin 2L, в знаменателе 1- cosL. Эта дробь равна -2 sinL. Как я ее ни кручу , создается впечатление, что здесь где-то опечатка.
помогите. разобраться. всем большое спасибо!
помогите. разобраться. всем большое спасибо!
читать дальше
ДД!
Помогите найти ошибку в производной, если она есть. Мое решение в приложении (знаменатель роли не играет до последнего действия, поэтому я его не пишу).
Суть проблемы в том, что онлайн-калькуляторы для производной выдают точно такой же ответ, только со знаком минуса (но без подробного решения).
Если же подставлять построчно мое решение (до 6 строки включительно) в онлайн-калькуляторы для упрощения выражений, то результат тоже с минусом. Если дальше 6 строки, то вообще другой ответ.
Я уже всю голову сломал, не могу понять как такое возможно.
Спасибо
ДД!
Помогите найти ошибку в производной, если она есть. Мое решение в приложении (знаменатель роли не играет до последнего действия, поэтому я его не пишу).
Суть проблемы в том, что онлайн-калькуляторы для производной выдают точно такой же ответ, только со знаком минуса (но без подробного решения).
Если же подставлять построчно мое решение (до 6 строки включительно) в онлайн-калькуляторы для упрощения выражений, то результат тоже с минусом. Если дальше 6 строки, то вообще другой ответ.
Я уже всю голову сломал, не могу понять как такое возможно.
Спасибо
среда, 20 апреля 2016
`3^(log_3^2(x))+x^(log_3(x))=162`
Не могу сообразить, какую замену сделать. Пытался сделать замену `t=log_3(x)`, но не получается. Пробовал взять логарифм от обоих частей по основанию 3, тоже ни к чему не прихожу. Прошу помощи.
Не могу сообразить, какую замену сделать. Пытался сделать замену `t=log_3(x)`, но не получается. Пробовал взять логарифм от обоих частей по основанию 3, тоже ни к чему не прихожу. Прошу помощи.
You have nothing to fear, if you have nothing to lose
Други, некоторое время назад я решила подтянуть свою эрудицию и вот добралась до математики. Меня интересует такой вопрос: можно ли как то систематизировать все разделы математики от простого к сложному? Я накачала кучу учебников и нигде ничего похожего, а у меня так мозг устроен , что отрывочную инфу я не понимаю(и еще я гуманитарий).
Короче, можете мне помочь?
Как я поняла сейчас:
Сначала идут цифры и их типы(арифметика)
Потом соотношения чисел и операции с ними(алгебра, математический анализ)
Потом формы и пространства(геометрия)
А вот дальше что? Дискретная математика это например что? А теория игр куда относится? Я заглядывал в вики, если чо, но мне не понятно.
Короче, можете мне помочь?
Как я поняла сейчас:
Сначала идут цифры и их типы(арифметика)
Потом соотношения чисел и операции с ними(алгебра, математический анализ)
Потом формы и пространства(геометрия)
А вот дальше что? Дискретная математика это например что? А теория игр куда относится? Я заглядывал в вики, если чо, но мне не понятно.
`int_2^3 (arctg (19x))/((x-2)exp(12x))dx`
Пытаюсь воспользоваться признаком сравнения. Т.к. `|arctg (19x)|<=pi/2`, то
`(arctg (19x))/((x-2)exp(12x))<=pi/2*1/((x-2)exp(12x))<=pi/2*1/(x-2)`
Несобственный интеграл `int_2^3 dx/(x-2)` расходится.
Можно ли сказать, что исходный интеграл расходится?
Ведь в признаке сравнения:
Из того, что `f(x)<=g(x)` и `int_a^b f(x)dx` расходится, то расходится и `int_a^b g(x)dx`.
У меня же получилась оценка в другую сторону.
Пытаюсь воспользоваться признаком сравнения. Т.к. `|arctg (19x)|<=pi/2`, то
`(arctg (19x))/((x-2)exp(12x))<=pi/2*1/((x-2)exp(12x))<=pi/2*1/(x-2)`
Несобственный интеграл `int_2^3 dx/(x-2)` расходится.
Можно ли сказать, что исходный интеграл расходится?
Ведь в признаке сравнения:
Из того, что `f(x)<=g(x)` и `int_a^b f(x)dx` расходится, то расходится и `int_a^b g(x)dx`.
У меня же получилась оценка в другую сторону.
Когда женщина перестает быть юной и прелестной, она становится мудрой и роскошной
Здравствуйте!
Подскажите по решению, я чего-то туплю)
online-tusa.com/tasks/2545_1_4_0
Задача такая: С какой силой надо удерживать груз весом P, чтобы он не сползал вниз по наклонной плоскости (угол наклона альфа)?
Я делаю что ось х идет по наклонной плоскости (сонаправлена с искомой силой F), тогда надо найти проекцию P на эту ось, т.е. Px
Но Px ведь гипотенуза, значит должна равняться P/sin a, а в ответе наоборот умножить... Что не так?
Подскажите по решению, я чего-то туплю)
online-tusa.com/tasks/2545_1_4_0
Задача такая: С какой силой надо удерживать груз весом P, чтобы он не сползал вниз по наклонной плоскости (угол наклона альфа)?
Я делаю что ось х идет по наклонной плоскости (сонаправлена с искомой силой F), тогда надо найти проекцию P на эту ось, т.е. Px
Но Px ведь гипотенуза, значит должна равняться P/sin a, а в ответе наоборот умножить... Что не так?
вторник, 19 апреля 2016
Здравствуйте!
Имеется функция `f(z, \alpha) = z/((1+z*e^{-i \alpha})^2)`. Нужно найти в какую область она отображает единичный круг.
Собственно, ответ известен, эта функция отображает единичный круг на плоскость с разрезом `t*e^{i \alpha}`, где `t \in [1/4, +\infty)`.
Вводя параметрическое представление окружности `z=e^{i \varphi}`, где `0<=\varphi<=2 \pi`и подставляя ее в функцию `f(z, \alpha)`,у меня не получается луч, данный в ответе... Может что-то упускаю?
Имеется функция `f(z, \alpha) = z/((1+z*e^{-i \alpha})^2)`. Нужно найти в какую область она отображает единичный круг.
Собственно, ответ известен, эта функция отображает единичный круг на плоскость с разрезом `t*e^{i \alpha}`, где `t \in [1/4, +\infty)`.
Вводя параметрическое представление окружности `z=e^{i \varphi}`, где `0<=\varphi<=2 \pi`и подставляя ее в функцию `f(z, \alpha)`,у меня не получается луч, данный в ответе... Может что-то упускаю?
`int_{1}^{+infty} (dx)/sqrt(x(x+1)(x+2))`, получилось, что сходится через предельный признак сравнения (`g(x)=1/x^(3/2)`).
`int_{1}^{+infty} (sqrt(x^3)+root(3)(x^2))/(x^3+3x+1)dx`, получилось, что сходится через предельный признак сравнения (`g(x)=1/x^(3/2)`).
А как сделать через признак сравнения?
читать дальше
`int_{1}^{+infty} (sqrt(x^3)+root(3)(x^2))/(x^3+3x+1)dx`, получилось, что сходится через предельный признак сравнения (`g(x)=1/x^(3/2)`).
А как сделать через признак сравнения?
читать дальше