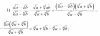В10

[diyno4ka]

Научная конференция проводится в 3 дня. Всего запланировано 60 докладов - в первый 15 докладов, остальные распределены поровну на второй и третий дни. Порядок выступлений определяется жеребьевкой. Найти вероятность выступления профессора М. в последний день.

на два последних дня остается 45 докладов

@темы: Теория вероятностей, ЕГЭ

---

Тригонометрические неравенства

[SeeeT]

Объясните пожалуйста,

1.5 мб.

как вычисляются эти точки, при решении тригонометрических неравенств?

`cos x < - 1/2`

@темы: Тригонометрия

---

Тхэквондо

[wpoms.]

`2n` мужчин и `2n` женщин приняли участие в круговом (каждый встречается с каждым по одному разу) турнире по Тхэквондо. Ниже приводятся правила начисления очков. (A) Если встречаются двое мужчин или две женщины, то за победу дают `3` очка, за проигрыш `0` очков, за ничью оба соперника получают `1` очко. (B) Если встречаются мужчина и женщина, то, если побеждает женщина, то она получает `3` очка, в случае проигрыша она не получает очков, за ничью она получает `2` очка, если побеждает мужчина, то он получает `2` очка, в случае поражения или ничьей он не получает очков. По завершении турнира подсчитываются очки, набранные каждым участником. Обозначим количество встреч, которые завершились вничью, как `P`, а общее количество встреч обозначим как `Q`. Если лучший участник соревнования набрал `4n-1` очков, то чему равно `P/Q`?

@темы: Порешаем?!

---

[е в степени икс]

Задание:
Составить уравнение плоскости, проходящей через прямую `{(X = 0),(Y ),(Y + Z = 1):}` и отсекающей от координатных плоскостей пирамиду объемом `V=6`.
Попытка решения:
Вот все, что пришло в голову..
Обозначим точки, в которых плоскость пересекается с осями координат A(X_A, 0, 0), B(0, X_B, 0), C(0, 0, X_C)
Тогда объем пирамиды будет равен одной шестой смешанного произведения векторов ОА ОВ и ОС и равен шести.
Из этого у меня получилось, что `X_A*X_B*X_C=1`
А дальше мыслей никаких..

@темы: Векторная алгебра

---

[Amicus Plato]

В математике нет символов для неясных мыслей. Анри Пуанкаре

29 апреля исполнилось 159 лет со дня рождения одного из величайших математиков Анри Пуанкаре.

Уже говорила, но повторю еще раз — чем больше масштаб ученого, тем труднее написать о нем лаконично и полно. Ничего удивительного в этом нет. Но для летописца это немалая трудность.
Цитировать всю Википедию не буду — очень длинно... Но буду рекомендовать прочитать, потому что очень интересно!
А сюда только небольшие выдержки помещу.

---

Википедия

Жюль Анри Пуанкаре (фр. Jules Henri Poincaré; 29 апреля 1854, Нанси, Франция — 17 июля 1912, Париж) — французский математик, механик, физик, астроном и философ. Глава Парижской академии наук (1906), член Французской академии (1908) и ещё более 30 академий мира, в том числе иностранный член-корреспондент Петербургской академии наук (1895).
Историки причисляют Анри Пуанкаре к величайшим математикам всех времён. Он считается, наряду с Гильбертом, последним математиком-универсалом, учёным, способным охватить все математические результаты своего времени. Его перу принадлежат более 500 статей и книг.

«Не будет преувеличением сказать, что не было такой области современной ему математики, „чистой“ или „прикладной“, которую бы он не обогатил замечательными методами и результатами».
(Колмогоров А. Н., Юшкевич А. П. (ред.) Математика XIX века.)

Среди его самых крупных достижений:

• Создание топологии.
• Качественная теория дифференциальных уравнений.
• Теория автоморфных функций.
• Разработка новых, чрезвычайно эффективных методов небесной механики.
• Создание математических основ теории относительности.
• Наглядная модель геометрии Лобачевского.

Статья в Википедии большая и подробная Читать полностью
Я выложу только "веселые картинки".
1. Топологическое преобразование тора в кружку


2. Хаотическое движение в задаче трёх тел (компьютерное моделирование)


Научные термины, связанные с именем Пуанкаре

• Гипотеза Пуанкаре
• Группа Пуанкаре
• Двойственность Пуанкаре
• Лемма Пуанкаре
• Метрика Пуанкаре
• Модель Пуанкаре пространства Лобачевского
• Нормальная форма Пуанкаре — Дюлака
• Отображение Пуанкаре
• Последняя теорема Пуанкаре
• Сфера Пуанкаре
• Теорема Пуанкаре — Бендиксона
• Теорема Пуанкаре — Вольтерра
• Теорема Пуанкаре о векторном поле
• Теорема Пуанкаре о возвращении
• Теорема Пуанкаре о скорости роста целой функции
• Теорема Пуанкаре о классификации гомеоморфизмов окружности
• Теорема Пуанкаре — Биркгофа — Витта

и многие другие.

Ну и напоследок две книги

Пуанкаре А. (Poincare H.) О науке Книга включает четыре произведения выдающегося французского математика Анри Пуанкаре (1854-1912): «Наука и гипотеза», «Ценность науки», «Наука и метод», «Последние мысли», о которых идет речь, давно уже стали , которые посвящены рассмотрению путей познания в математике, механике, физике. Последние русские переводы этих работ выходили около 60 лет назад; они давно стали библиографической редкостью и мало доступны современному читателю. Для математиков, физиков, механиков, философов. Скачать (djvu, 13 Мб) libgen.org

Тяпкин А., Шибанов А. Пуанкаре (Серия ЖЗЛ) Книга доктора физико-математических наук А. А. Тяпкина и кандидата физико-математических наук А. С. Шибанова посвящена выдающемуся французскому ученому Анри Пуанкаре, оставившему фундаментальные труды практически во всех отраслях точного естествознания конца XIX -начала XX века. Именно в его работах была сформулирована специальная теория относительности, он обосновал математический аппарат небесной механики, создал качественную теорию дифференциальных уравнений, заложил основы топологии. Скачать (djvu, 9 Мб) libgen.org

Больше книг Пуанкаре и о нем можно найти здесь.

Про гипотезу Пуанкаре, Григория Перельмана и другое ничего писать не буду...
А нет! Буду!

Владимир Успенский: О математике в культуре и гипотезе Пуанкаре

По ссылке можно и стенограмму почитать.

@темы: История математики, Люди

---

Несобственный интеграл от разрывной функции

[Marina Petrelli]

Здравствуйте! Проверьте пожалуйста правильность решения.
`int_{0}^{1} (x^3+x^(1/3)-2)/(x^(3/5)) dx= int_{0}^{1} ( x^3/x^(3/5)+x^(1/3)/x^(3/5)-2/x^(3/5)) dx= int_{0}^{1} (x^(12/5)+x^(-4/15)-2/x^(3/5)) dx` В точке `a=0` - разрыв, обращённый в бесконечность. => `lim t->{0+0} int_{t}^{1} x^(12/5)+x^(-4/15)-2/x^(3/5) dx = x^(2/5)lim t->{0+0} ((5/17)x^3+(15/11)x^(1/3)-5) | t..0`
здесь `{0..1}` и `{t..1}` - пределы интегрирования.
Далее, я подставляю единицу и конечный ответ `-625/187`

@темы: Несобственные интегралы

---

идея решения.

[соль_по_вкусу]

нужна помощь в решении. идея, вектор, в котором надо танцевать - что угодно, ибо надо сдавать.

`x'=ax^1/3+f(x)`
`a AA RR`
`f in C^infty`

@темы: Дифференциальные уравнения, Олимпиадные задачи, Задачи с параметром

---

Площадь и длина через интеграл

[tenacity]

Такие три задания:
1) найти площадь (параметрическ.): `{(x(t) = 4(cos t)^3),(y = 8(sin t)^3),(y >= 3sqrt(3)):}`
2) длину (в декартовой системе координат): `y(x) = 1 + e^(-2x)`, где `x in [ -1/4*ln(15/4); - 1/4*ln(3/4)]`
3) и длину (параметрич.): `{(x(t) = 3*(2cos t - cos(2t)) ), (y(t) = 3*(2sin t - sin (2t)) ):}`, где `t in [0;pi/4]`
через интегралы.

картинка

Я вроде как решила третье, но не уверена в правильности решения.

3

И начала решать первое, но застопорилась и не знаю что делать с интегралом дальше.

1

А за второе вообще не знаю, как браться. Буду очень благодарна если кто проверит/подскажет.

@темы: Интегралы

---

Условно-досрочный, vol.2

[webmath]

Скачать:
www.mapleprimes.com/posts/146236-Finish-Of-The-...

@темы: ЕГЭ

---

Помогите исправить....

[jasenka88]

Прорешала огромное кол-во задач на эту тему, но вот застопорила одна задача.... все вроде понятно, но ответ никак не хочет сходится....

Задача:
Найти циркуляцию векторного поля а по контуру Г непосредственно и по теореме Стокса.

а: 2zi+yzj-xk

Г: x=y^2+z^2, x=9.

Контур получается окружность с радиусом 3.

При непосредственном вычислении получается ответ =-144

По теореме Стокса беру за плоскость x=9, а значи нормаль n={1,0,0} и ответ выходит -36....
(когда за плоскость беру параболойд, ответ еще страшнее...что-то не сходится совсем)
Решения прикрепляю...
Подскажите, пожалуйста, где ошибка, измучилась вся(((

http://static.diary.ru/userdir/3/1/3/8/3138938/78352677.jpg

@темы: Теория поля, Приложения определенного интеграла, Векторный анализ

---

Полярные координаты

[tenacity]

Вычислить площадь фигуры в ПСК, заданной следующими уравнениями
`p=4`
`p=4sin (varphi)`

что есть

Проблема в том, что я даже не понимаю, какой получается фигура и какие у нее пределы интегрирования. Попыталась начертить, вышло что-то вроде, но почему-то мне кажется, что неверно.

@темы: Интегралы, Линии в полярной системе координат

---

Делимость

[wpoms.]

Пусть `a`, `b` - взаимно простые целые числа и `m` - целое. Докажите, что если `5|ma^2 + b^2`, то существует целое `n`, для которого `5|m-n^2 `

@темы: Теория чисел

---

Проверьте, пожалуйста. Дифференциальные уравнения.

[Miriada11]

1.` y'=(2*y+1)*ctg(x),` ` y(Pi/4)=0,5`
Решение:

`dy=(2*y+1)*ctg(x)`

`dy /( 2*y+1)= ctg(x)dx`

`int (dy /( 2*y+1))= int ctg(x)dx`

`(1/2)ln(|2*y+1|)= int ( cosx dx/ sinx)`

`(1/2)ln(|2*y+1|)= int (d(sinx)/sinx)`

`(1/2)ln(|2*y+1|)=ln|sinx| +ln|C_1|

`sqrt(|2*y+1|)=|C_1*sinx|`

`|2*y+1|=(C_1^2)*sin^2x`

` 2*y+1= (+-) (C_1^2)sin^2x`

`2*y+1=C*sin^2x

`2*y=C*sin^2x-1`

Общий интеграл: `y=(C*sin^2x-1)/2`

C=4, тогда частное решение: `y=(4*sin^2x-1)/2`

2. `(x^2)*y'=2*x*y+y^2,` `y(1)=1`

Решение:

`y'=2(y/x)+(y/x)^2`, пусть `(y/x)=t`, тогда `y=t*x`

`t'*x+t=t^2+t`

`(x/dx)=(t^2+t)/dt`

`int (dx/ x)= int dt/(t^2+t)`

`int (dx/ x)= int d(t+1/2)/(((t^2+t/2)^2)-1/4)`

`ln|x|=ln|t/(t+1)|+ln|C1|`

`x=(C_1*t)/(t+1)`, тогда после обратной замены `x=(C_1*y)/(y+x)`,

` y=x^2/(C_1-x)`- общее решение,

`C_1=2`, ` y=x^2/(2-x)`- частное.

3. `3*y'+y*cosx=sin2x`, `y(0)=0`

Решение:
`y=U*V`

`U'*V+U*V'+U*V*cosx=sin2x`

`V'+Vcosx=0`

`V'=-V*cosx`

`ln|V|=-sinx`

`V=e^(-sinx)`

`U'*e^(-sinx)=sin2x`

`dU=((e^sinx)*sin2x)dx`

`int dU=int( (e^(-sinx))*2*sinx*cosx)dx = 2 int (e^(-sinx)*sinx) d(sinx) = |` пусть` sinx=t| = 2 int ((e^t)*tdt) =`

` | U1=t, \ dU1 =dt, \ dV1=(e^t)dt, \ V1=e^t|=2(e^t)*t-2e^t=2(e^sinx)sinx-2(e^sinx)+C`

`y=e^(-sinx)*(2(e^sinx)sinx-2(e^sinx)+C)=2sinx-2+C*e^(-sinx)`- общее решение.

C=2, частное решение: `y=2sinx-2+2*e^(-sinx).

4. `(1-x^2)*y'-xy=xy^2`, ` y(0)=0,5`

Решение:

`y'-(xy)/(1-x^2)=(xy)^2/(1-x^2)^2`

`y=U*V`

`U'V+UV'-(xUV)/(1-x^2)=(xUV)^2/(1-x^2)^2`

`V'-(xV)/(1-x^2)=0`

`dV/dx=(Vx)/(1-x^2)`

`int dV/V=int (xdx/(1-x^2))`

`ln|V|=(-1/2)*int(d(x^2)/(x^2-1))`

`ln|V|=ln(1/sqrt(|x^2-1|))`

`V=1/sqrt(x^2-1)`

`{U'}/sqrt(x^2-1)=(xU^2)/(x^2-1)(1-x^2)`

`{U'}/sqrt(x^2-1)= - (xU^2)/(x^2-1)^2`

`int dU/U^2=- int ((( x* sqrt(x^2-1))/ (x^2-1)^2) dx`

` 1/U=sqrt(x^2-1) +C1`

`U=1/sqrt(x^2-1) +C`

`y=(1/sqrt(x^2-1))*(1/sqrt(x^2-1)+C)=(1/(x^2-1))+C/sqrt(x^2-1)` -общее решение

При подстановке начальных условий под корнем получается отрицательное число: `1/2=-1+C/sqrt(0-1)`

5. `y'''=6*x^(-3)`, `y(1)=2, y'(1)=y''(1)=1`

Решение:

`y''=(-3/x^2)+C1`, `C1=4`, ` y''=(-3/x^2)+4`

`y'=(1/x)+C1x+C2`, ` C2=-4`, `y'=(1/x)+4x-4`

`y=ln|x|+(C1x^2)/2+С2x+С3` ,` C3=4`, `y=ln|x|+(4x^2)/2-4x+4`

6. ` x^3*y''+ x^2*y'=1` , `y(1)=y'(1)=0`

Решение:

Замена:` y'=P(x)`, `y''=P'(x)`


` x^3*P'+ x^2*P=1`

`P'+P/x=1/x^3`

`P=UV`

`U'V+UV'+(UV)|x=1/x^3`

`V'+V/x=0`

`int (dV/V)=-int(dx/x)`

`V=1/x`

`{U'}/x=1/x^3`

`dU=(xdx)/x^3`

`U=(-1/x)+C`

`P=y'=(1/x)*((-1/x)+C)=-1/x^2+ C/x`,` C=1`

`y=1/x + Cln|x| +C1`, ` C1=-1`

7. `x^3y''=-1`, `y(0,5)=y'(0,5)=1`

Решение:
`y''=-1/x^3`

`y'=(1/2x^2) +C1`, `C1=-1`, `y'=(1/2x^2) -1`

`y=(-1/2x)+C1x+C2`

`C2=5/2`

`y=(-1/2x) -1+5/2`

8. `y"+2y'+y=4e^(-x)`, `y(0)=1`, `y'(0)=0`
Решение:

`lambda^2+2lambda+1=0`
`lambda1,2=-1, тогда

Общее решение: `z=C1e^(-x)+C2*x*e^(-x)`

Частное решение представим в виде:
`tilde(y)=Ae^(-x)*x`

`tilde(y)'=-Ae^(-x)*x+Ae^(-x)`

`tilde(y)"=Ae^(-x)*x- Ae^(-x)-Ae^(-x)`

`Ae^(-x)*x- Ae^(-x)-Ae^(-x)+2Ae^(-x)*x+2Ae^(-x)+Ae^(-x)*x=4e^(-x)` - тут всё сокращается. Ошибку не могу найти до сих пор.

9. `y"+4y'+4y=exp(-2x)*x^(-3)`, `y(1)=3/(2e^x)`, `y'(1)=0`

Решение:
`lambda^2+4lambda+4=0`
`lambda1,2=-2`, тогда

Общее решение:` z=C1e^(-2x)+C2*x*e^(-2x)`

Частное решение представим в виде:
`tilde(y)=(Ax^3+Bx^2+Cx+D) *e^(-2x)*x` - до сих пор правильно?

@темы: Дифференциальные уравнения

---

подскажите начало нахождения площади (№4)

[Nicas]

`D: (x^2+y^2)^2 = 4x^2 + y^2 ` `S(D) `- ?

функция ж получается задана не явно,получается нужно выразить игрек в ` (x^2+y^2)^2` и в `4x^2 + y^2` ?

@темы: Интегралы

---

Погорелов, равенство треугольников

[remonortsa2]

Вот определения равенства треугольников из учебника Погорелова.

Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.

Никак не могу понять, что вкладывается в понятие соответствующие стороны и соответстующие углы. Есть какое-то определение этому или это просто интуитивные понятия? Соответстующие углы - те, которые лежат против большей стороны?

А почему употреблено слово соответствующие? А если просто так:
Треугольники называются равными, если у них стороны и углы равны.

Или в этом определении мы неявно используем, что против равных углов будут лежать равные стороны (которое, наверное, доказывается где-то там дальше в курсе)

Вот два треугольника.

Понятно, что угол BAC = углу `B_1A_1C_1` (верхние два треугольника), значит они соответствующие. А можем мы указать соответствущие углы не указывая соответствующие стороны?

А соответствующие стороны - те, которые равны?..

В общем, путаница какая-то.

@темы: Планиметрия

---

Ур-я мат. физики

[Afu-Ra]

Доброе утро, помогите с задачкой.

4. Найти концентрацию в растворе, помещенном внутрь цилиндрической трубки `0<=p<=b` с непроницаемой стенкой, если начальное распределение концентрации задано неравенством:

`C|_(t=0) = {(C_0, 0<=p<=c), (0, c<p<=b):}`

Решение

Посмотрите пожалуйста правильно ли я поставил задачу. Не буду пока что дальше решать, вдруг здесь ошибся.

@темы: Уравнения мат. физики

---

Борьба за компьютер с принтером

[wpoms.]

В круговом турнире с n игроками ( `n >= 100` ) за победу начисляют 2 очка, за ничью 1 очко и за поражение очки не начисляются. После завершения турнира и подведения итогов объявили условия получения призов. а) Для получения компьютера группой игроков необходимо, чтобы среди любых 100 игроков был один игрок, который победил 99 других игроков, и один игрок, который проиграл 99 другим. б) Для получения принтера группой игроков необходимо, чтобы количество очков, набранных всеми игроками из этой группы, отличались друг от друга. Какое наименьшее количество игроков должно быть в группе, которая может гарантированно выиграть и компьютер и принтер?

@темы: Комбинаторика

---

Упростить выражение. класс 7-8

[Роун Мария]

(√a-√b)/∜a-∜b — (√a+∜ab)/∜a+∜b
У меня есть решение на это задание

вероятно,это крайне легко, но я уже битый час не могу понять, как это так решилось. Распишите,пжл,максимально подробно решение, а то я с ума сейчас сойду.

@темы: Школьный курс алгебры и матанализа, ЕГЭ

---

[Amicus Plato]

28 апреля исполнилось 107 лет со дня рождения выдающегося математика и логика Курта Гёделя.

Про таких выдающихся людей очень трудно писать — слишком уж много надо сказать, начав говорить...
Поэтому ограничусь немногим. Статьей из Википедии (содержащей жуткие биографические подробности), фотографиями, видео-роликом и ссылкой на лекцию А.Б. Сосинского о теореме Гёделя о неполноте. Такой вот план. А теперь его реализация.

Википедия
Курт Фридрих Гёдель (нем. Kurt Friedrich Gödel; 28 апреля 1906, Брюнн, Австро-Венгрия — 14 января 1978, Принстон, Нью-Джерси) — австрийский логик, математик и философ математики, наиболее известный сформулированной и доказанной им теоремой о неполноте.

Биография
Курт Гёдель родился 28 апреля 1906 года в австро-венгерском (моравском) городе Брюнн (ныне Брно, Чехия), в немецкой семье. Отец Курта, Рудольф Гёдель, был управляющим текстильной фабрики.
Окончив школу в 1923 году, Гёдель поступил в Венский университет. Там он два года изучал физику, но затем переключился на математику. В 1929 году защитил диссертацию и в 1930 году начал преподавать в Венском университете, участвуя в семинарах Венского кружка неопозитивизма. В 1934 году совершил поездку в США (Принстонский университет), где прочитал курс лекций «О неразрешимых теоремах формальных математических систем». В 1938 году он женился на Адель Поркерт, с которой познакомился в Венском клубе еще в 1927 году.
В 1940 году он уехал в США, причём из-за опасности пути через Атлантику во время войны поехал через СССР и Японию. В США он получил работу в знаменитом Институте перспективных исследований (Принстонский университет). В 1951 году Гёдель получил высшую научную награду США – Эйнштейновскую премию, а в 1974 году – Национальную Медаль Науки.

Болезнь и смерть
Ещё с 30-х годов у Гёделя обнаруживались признаки психических проблем, которые обычно носили скрытый характер, проявляясь в частых беспокойствах и излишней подозрительности, но в периоды обострений принимали более явные, навязчивые формы. Так, в 1936 году у него развился параноидальный страх отравления. Опорой Гёделя в нелёгкое время была его жена Адель, кормившая его с ложки и буквально выходившая мужа. Из сохранившихся записей библиотечных запросов этого периода известно, что он изучал литературу по душевным расстройствам, фармакологии и токсикологии (особенно характерно неоднократное обращение к техническому справочнику по отравлениям угарным газом), что лишь осложняло впоследствии его лечение.
Позже, в Принстоне (1941), несмотря на улучшение общего состояния, Гёдель по-прежнему испытывал дискомфорт от присутствия агрегатов, способных, по его мнению, испускать отравляющие газы. По этой причине он даже распорядился вынести из их с Аделью квартиры холодильник и радиатор. Его одержимость свежим воздухом и подозрения по поводу холодильника сохранялись до конца жизни, а периоды умеренного оздоровления и ухудшения душевного состояния сменяли друг друга. Последние, впрочем, происходили всё чаще и были тяжелее. Так, кризис 1970-го года оказался гораздо хуже такового в 1936-м и сопровождался галлюцинациями, параноидальным поведением по отношению к докторам и коллегам. Стремительно ухудшалось и состояние здоровья Адель, теперь она не могла ухаживать за ним так, как раньше, а он, в свою очередь, — за ней. Огромную поддержку оказывал друг Гёделя Оскар Моргенштерн.
В феврале 1976 года паранойя Гёделя опять обострилась, начал снижаться вес и его уговорили на госпитализацию. Однако уже через неделю, даже не выписавшись, он вернулся домой. Подозрения касались теперь и жены — Моргенштерну и другим людям он рассказывал, что та якобы раздала в его отсутствие все его деньги. В июне Адель была госпитализирована (до августа). Гёдель проводил с ней, по-видимому, достаточно много времени и плохо питался. Осенью он ненадолго снова попал в больницу, где, как он сообщил, его якобы пытались убить. После возвращения домой состояние не улучшалось. Несмотря на уговоры друзей, от очередной госпитализации он отказывался.
В июле 1977 года Адель вновь попала в больницу, где пробыла до декабря. 26 июля умер Моргенштерн. Это событие и отсутствие жены оказали решающее влияние на состояние Гёделя в последующие несколько месяцев — анорексия и паранойя прогрессировали всё активнее. 29 декабря, следуя настояниям жены, возвратившейся около недели до того, Гёдель согласился на госпитализацию. Однако врачи никакую существенную помощь оказать уже не могли. Учёный скончался от «недоедания и истощения», индуцированных «расстройством личности», 14 января 1978 года в Принстоне, штат Нью-Джерси.

Научное наследие
Гёдель был логиком и философом науки. Наиболее известное достижение Гёделя — это сформулированные и доказанные им теоремы о неполноте, опубликованные в 1931 году. Одна из них гласит, что любая эффективно аксиоматизируемая теория, в достаточно богатом языке, достаточном для определения натуральных чисел и операций сложения и умножения является неполной либо противоречивой. Неполнота означает наличие высказываний, которые нельзя ни доказать, ни опровергнуть, исходя из аксиом этой теории. Противоречивость — возможность доказать любое высказывание: как истинное так и ложное. Эффективная аксиоматизируемость понимается как возможность алгоритмически решить, является ли данное утверждение аксиомой. Доказанные Гёделем теоремы имеют широкие последствия как для математики, так и для философии (в частности, для онтологии и философии науки).
Кроме того, Гёделю принадлежат работы в области дифференциальной геометрии и теоретической физики. В частности, он написал работу по общей теории относительности, в которой предложил вариант решения уравнений Эйнштейна, из которого следует, что строение вселенной может иметь такое устройство, в котором течение времени является закольцованным (метрика Гёделя), что теоретически допускает путешествия во времени. Большинство современных физиков считают это решение верным лишь математически и не имеющим физического смысла.

Фото

Почти все фото взяты с этого сайта: persons-info.com/index.php?kwdtranslit=logika&p...

Видео (оценить его не возьмусь).


Ссылка на лекцию А.Б. Сосинского о теореме Гёделя о неполноте.
eek.diary.ru/p183499318.htm

@темы: История математики, Люди

---

Пожалуйста,наведите на мысль.Заранее благодарю

[docfedia]

Напишите уравнение гиперболы,проходящей через точку(1,1),касающейся ОХ в точке (3,0),имеющей ОУ своей асимптотой

@темы: Аналитическая геометрия