[Ka.]

при любых K выражение

K^3-K

делится на 6

то что делиться я проверила на 2, 3, 4 , 5
а откуда эту 6 выудить? у меня эта 6 только при второй производной получается

---

[Makha]

Помогите, пожалуйсте, нужно записать первые четыре члена ряда. Исследовать сходимость...
Сумма от 1 до бесконечности 2 в степени n, разделенное на 100n.

Это Высшая математика, контрольная нужно до 1 августа....

@темы: Ряды

---

Новости

[Robot]

Женщины-математики стали жертвами стереотипов:

В ходе исследований, проведенных под руководством профессора психологии Дженет Хайд (Janet Hyde) среди разных возрастных групп учеников в американских школах, было выявлено, что и мальчики, и девочки решают математические задачи примерно на одинаковом уровне, пишет PhysOrg.
Причина распространенного мнения о более низких способностях слабого пола к точным дисциплинам лежит скорее в области психологии, считает проф. Хайд. Мнение о невысоких математических способностях женщин, внушаемое школьни… полный текст

Источник: CNews

Гипотеза Римана осталась недоказанной

Несколько дней назад специалист по теории чисел Сян-Джин Ли заявил, что ему удалось доказать гипотезу Римана о нетривиальных нулях дзета-функции, то есть решить задачу, признанную одной из важнейших научных проблем тысячелетия. Свое доказательство он описал в статье "A proof of the Riemann hypothesis", опубликованной в базе данных Корнельского университета.
Доказательство Ли основано на работах известного французского математика Алана Конна (Alain Connes), автора основополагающих трудов по некоммутативной геометрии...полный текст

Источник: CNews

О гипотезе Римана, 1859 [теория чисел] мы уже писали в нашем сообществе, как об одной из 7 величайших математических загадок тысячелетия, за решение каждой из которой Институт математики Клэя объявил о награде в $1 млн. В 1900 Давид Гильберт включил гипотезу Римана в список 23 нерешённых проблем как часть восьмой проблемы совместно с гипотезой Гольдбаха.
Считается, что распределение простых чисел среди натуральных не подчиняется никакой закономерности. Однако немецкий математик Риман высказал предположение, касающееся свойств последовательности простых чисел. Если гипотеза Римана будет доказана, то это приведет к революционному изменению наших знаний в области шифрования и к невиданному прорыву в области безопасности Интернета.
Большинство математиков верят, что гипотеза верна. На 2004 год проверены более 10¹³ первых решений
Знаменит ответ Гильберта на вопрос о том, каковы будут его действия, если он по какой-то причине проспит пятьсот лет и вдруг проснется. Математик ответил, что самым первым делом он спросит была ли доказана гипотеза Римана.
Другой такой величайшей математической загадкой является гипотеза Кука, 1971 (Равенство классов P и NP)
Допустим, находясь в большой компании, Вы хотите убедиться, что там же находится Ваш знакомый. Если Вам скажут, что он сидит в углу, то Вам достаточно доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствии этой информации Вы будете вынуждены обойти всю комнату, рассматривая гостей. Точно так же, если кто-то сообщит Вам, что число 13717421 можно представить, как произведение двух меньших чисел, непросто быстро убедиться в истинности информации, но если Вам сообщат, что исходное число можно разложить на множители 3607 и 3803, то это утверждение легко проверяется с помощью калькулятора.
Это примеры иллюстрируют общее явление: решение какой-либо задачи часто занимает больше времени, чем проверка правильности решения. Стивен Кук сформулировал проблему: может ли проверка правильности решения задачи быть более длительной, чем само получение решения, независимо от алгоритма проверки. Эта проблема является одной из нерешенных проблем логики и информатики. Ее решение могло бы революционным образом изменить основы криптографии, используемой при передаче и хранении данных.
В сообществе Поп-математика для взрослых детей  Amicus Plato, известная нам всем как  Дилетант, выложила цикл статей, которые позволяют поглубже разобраться в проблеме Кука (P=?NP).
Рассказ про алгоритмическую сложность, классы P и NP, и про NP-полноту

Продолжение рассказа про алгоритмическую сложность, классы P и NP и про NP-полноту I
Продолжение рассказа про алгоритмическую сложность, классы P, NP, и про NP-полноту II
Продолжение рассказа про алгоритмическую сложность, классы P, NP и про NP-полноту III
Алгоритмическая сложность. Лирическое отступление
Время работы алгоритмов
Класс NP
NP-полнота, NP-полные задачи и булевы формулы

Еще одна запись об NP-полноте (не обещаю, что последняя)))
Наконец-то! P?=NP и институт Клэя

UPD. Еще кое-что об институте Клэя

Институт Clay открыл электронную библиотеку

Американский Институт математики Clay разместил в интернете бесплатную электронную библиотеку.
Материалы библиотеки опубликованы на сайте института www.claymath.org/library в формате pdf. Среди них - книги, тексты публичных лекций и статьи. Все они ранее выходили в "бумажном" виде, но не были доступны для широкой публики… полный текст

Источник: CNews

@темы: Интересное в @дневниках, Новости, Наука

---

Понравилась задачка с одного форума..

[Robot]

Дана последовательность, где первый член 3¹⁰⁰, а каждый следующий равен сумме цифр предыдущего. Найти десятый член последовательности

@темы: Школьный курс алгебры и матанализа, Теория чисел

---

[7XPEH7]

Есть 2, по-моему, идентичных интеграла


и на первый взгляд они мне показались простыми, но когда я начал их брать мне уже так не кажется.
Я не знаю, с какой стороны к ним подступиться, помогите, пожалуйста!

@темы: Интегралы

---

Интеграл

[7XPEH7]

Подскажите, пожалуйста, с чего начать при взятии этого

интеграла?

@темы: Интегралы

---

Научные и образовательные СМИ

[Robot]

NT-INFORM.RU - Новости научно-популярных СМИ
В мире науки
Журнал "В мире науки" (Scientific American) выходил с 1983 по 1993гг. и возобновил свою работу с 2003г. Издание адресовано как научной и технической интеллигенции, так и широкому кругу образованных читателей, стремящихся быть в курсе последних достижений мировой научной мысли. На его страницах активно обсуждаются наиболее актуальные проблемы современной науки, вопросы ее места и роли в современном мире, ответственности ученых за судьбы человечества, взаимодействия науки с обществом и государством. Мы публикуем также наиболее интересные статьи ведущих российских ученых, новости науки и научной жизни, рецензии на книги. Мы стремимся не только идти в фарватере современной науки, но и откликаться на животрепещущие вопросы современности, такие как, скажем, проблемы биотехнологии, демографии или образования. Журнал дает уникальную возможность ученым разных направлений утвердить свои концепции и открытия, полемизировать с оппонентами. Одна з наших основных задач - предоставление актуальной и достоверной научной информации, которую следует противопоставить мистическим и лженаучным представлениям, которые, к сожалению, получили в последнее время широкое распространение. Сейчас налицо, и не только в нашей стране, определенный мировоззренческий кризис: старое мировоззрение во многом рухнуло, новое еще не сформировалось. Как она будет зарождаться, какими силами? Журнал "В мире науки" стремится хотя бы отчасти заполнить образовавшийся концептуальный вакуум, способствовать созданию нового синтеза. (С.П.Капица)
Наука и жизнь
Журнал «Наука и жизнь» впервые вышел в свет почти 115 лет назад – в 1890 году в Москве. В 1934 году его издание возобновилось в Москве. И с тех пор «Наука и жизнь» остается самым известным и читаемым научно-популярным журналом в России. Журнал «Наука и жизнь» стал одним из первых российских изданий, у которого появился свой Интернет-сайт с полной версией электронного архива журнала. Случилось это в 1997 году по предложению одного из создателей русского Интернета Игоря Григорьевича Пасынкова, который затем помог разместить новое Интернет-издание на сервере компании «Релком» по электронному адресу nauka.relis.ru (впоследствии – www.nauka-i-zizn.ru). Структуру и дизайн первой версии сайта разработал заведующий отделом полиграфии журнала «Наука и жизнь» Сергей Сергеевич Величкин.
Со временем назрела необходимость создания полного электронного архива журнала, оснащенного поисковой системой. Кроме того, появилась потребность в интерактивных разделах и регулярно обновляющейся новостной ленте. В сентябре 1994 года Федеральное агентство по печати и массовым коммуникациям предоставило Автономной некоммерческой организации «Редакция журнала «Наука и жизнь» денежные средства на создание и развитие электронного архива и Интернет-портала на основе электронной версии журнала «Наука и жизнь». Так стартовал новый проект.
Сейчас посетители нового сайта журнала «Наука и жизнь» www.nkj.ru могут ознакомиться с текущими и архивными номерами журналов последних лет и осуществить поиск по архиву, узнать последние новости науки и техники, поучаствовать в работе «Дискуссионного клуба», задать вопросы специалисту в «Интернет-интервью» или ответить на вопросы редакции, узнать последние новости российской науки и техники в разделе «Новости и события» и многое другое. Пока не все содержание прежнего сайта перенесено в новый портал, поэтому посетители могут при необходимости обратиться к старой версии.
Квант
Первый номер "Кванта" вышел в 1970 году. Идею создания журнала высказал Петр Леонидович Капица в 1964 году, и она нашла благодарную почву среди энтузиастов, которые в те годы занимались организацией физико-математических школ-интернатов при крупнейших университетах, всесоюзных олимпиад, летних школ (да и время было исполнено надежд и всеобщего увлечения наукой).Возглавили журнал два выдающихся ученых — Исаак Константинович Кикоин и Андрей Николаевич Колмогоров. Так был создан первый в мире научный журнал для школьников, рассчитанный на массового читателя.
Материалы, накопленные в журнале за эти годы, бесценны. Не раз доводилось спрашивать молодых ученых, многого добившихся в науке, и замечательных учителей: "Что повлияло на выбор професии?" Ответы почти всегда были одни и те же: Учитель (школьный учитель, сумевший увлечь своим предметом) и "Квант".
Математическое Просвещение
Математическое просвещение — математический журнал (сборник статей), ныне издаваемый Московским Центром Непрерывного Математического Образования (МЦНМО) с периодичностью один номер в год. Сборник начинали издавать три раза, таким образом существуют три серии сборника. Текущая третья серия издается с 1997 года. Сборники третьей серии представляют собой связующее звено между специальной и популярной математической литературой. В сборники включаются статьи о новых фундаментальных результатах, новых направлениях развития чистой и прикладной математики, в том числе и переводы статей из популярных зарубежных математических изданий, таких как «American Mathematical Monthly», «Mathematical Intelligencer», «Mathematical Gazette» и «L’Enseignement mathematique». Помимо статей математического содержания, в сборниках публикуются материалы, отражающие реальное состояние преподавания математики в России (прежде всего, в специализированных классах и школах, а также в педагогических институтах и университетах).
Электронные версии сборника (все серии) свободно распространяются на официальном сайте.
Библиотека «Математическое просвещение»
Приложением к сборнику «Математическое просвещение» является серия брошюр Библиотека «Математическое просвещение», ориентированная в основном школьников и учителей. Материалы брошюр этой серии представляют собой углубленное изложение тем, поверхностно затрагиваемых в школьной программе, а также элементарное изложение основных результатов из областей математики, не вошедших в школьную программу.
NetBook - Научно-образовательный портал. На нем выложен ряд выпусков Соросовского образовательного журнала Соросовский Образовательный Журнал (СОЖ) был учрежден в 1995 г. Международной Соросовской Программой Образования в Области Точных Наук (ISSEP) по инициативе ее Председателя Правления и Генерального директора профессора В.Н. Сойфера, ставшего главным редактором журнала. Идея создания СОЖ родилась не случайно. В 1994 – 95 гг. ISSEP провела конкурсы среди преподавателей российских вузов на звание Соросовского Профессора и Соросовского Доцента. Лауреаты этих конкурсов – профессора и доценты, имеющие наиболее высокие в стране показатели уровня преподавания, в рамках программы Соросовских конференций стали читать лекции о последних достижениях естествознания для учителей во всех регионах России. Успех конференций был настолько большим, что стало очевидно: материалы лекций необходимо издать, чтобы обеспечить ими как можно большую аудиторию преподавателей и учащихся. Написание статей для СОЖ стало обязательным для Соросовских Профессоров, а впоследствии – и для Соросовских Доцентов. Начиная с 2000 г. для расширения научной тематики журнал стал заказывать отдельные статьи известным российским ученым, не участвовавшим в конкурсах ISSEP. Таким образом, вплоть до закрытия в конце 2001 г. в связи с прекращением финансирования, журнал публиковал статьи только лучших российских авторов.
Цель Соросовского Образовательного Журнала – сделать доступными всем учителям, школьникам и студентам России последние успехи в области естественных наук – биологии, химии, наук о Земле, физики и математики. В соответствии с этим были сформулированы главные требования для авторов журнала – описывать современную ситуацию в той области знания, где они работают, не ограничиваясь лишь собственными результатами, причем делать это на понятном старшеклассникам и студентам уровне, объясняя специфичную для данной науки терминологию. Таким образом, статьи СОЖ – это актуальные научные обзоры по самым разным областям естествознания, доступные для понимания старшеклассникам.
"Троицкий вариант" Газета, выпускаемая учеными и научными журналистами
Целевая аудитория
1. Научные работники, в особенности их активная, реформаторски настроенная часть - это предполагаемое ядро аудитории.
2. Все, кто проявляет интерес к науке, и к знаниям вообще. Особенно важно, чтобы газету читали студенты и старшеклассники.
Направления редакционной политики.
А. Основное стратегическое направление - противостояние наступающему невежеству. Просвещение в широком смысле слова: пробуждение интереса к науке и знаниям вообще, борьба с мракобесием разных видов. Публикация высококачественных просветительских статей, интервью с наиболее сильными учеными (включая тех, кто зарубежом), грамотные новости, высмеивание всяких псевдонаук и журналистских ляпов, юмор в стиле "физики шутят" и т.п.
Б. Актуальное направление - борьба с деградацией российской науки, угрожающей стать необратимой. Проблема российской науки не только в недостатке финансирования, но и в самой организации науки и, что хуже, в отсутствии полноценной научной среды.
Нужна незамедлительная реформа системы финансироваия и администрирования науки. Ключевые слова - конкурсность, независимая экспертиза, прозрачность, гранты, эволюционность. Повышение статуса и самостоятельности научных работников и групп, составляющих основную движущую силу науки. Этому направлению будет посвящен раздел "Бытие российской науки", который отчасти будет опираться на одноименный форум.
В. Местная специфика и вести из компактных научных ареалов (наукограды, крупные университеты и т.п.) - служит единению научного сообщества.
Г. Сотрудничество с другими изданиями просветительского и научно-ориентированного характера
НАУКА В "РУССКОМ ПЕРЕПЛЕТЕ"
Новости из мира науки и техники. Проект поддержан Международной Соросовской Программой образования в области точных наук.
Компьютерра: все новости про компьютеры, железо, новые технологии, информационные технологии
Журнал "Компьютерра"
Издательский дом "Первое сентября"
"Первое сентября" Математика
Портфолио "Первое сентября". Фестиваль исследовательских и творческих работ учащихся
Все новости образования "Первое сентября"
Газета «ИЗВЕСТИЯ»,приложение НАУКА
Lenta.ru Прогресс
«НЕЗАВИСИМАЯ ГАЗЕТА», приложение НАУКА

И не совсем СМИ, но не хочется потерять ссылку:
Математическое образование: прошлое и настоящее. Интернет-библиотека по методике преподавания математики
На сайте выложены журналы "Математика в школе" за ряд лет (ссылка)

@темы: Полезные и интересные ресурсы, Ссылки, Наука

---

Кому нечего делать...

[Robot]

Закачивая файлы на ifolder, вынуждена была принудительным порядком просматривать их рекламные файлы. Среди прочих - тесты на testsbox.ru. Обратила внимание на тест Математика, логика, интеллект testsbox.ru/tests/520 для детей старшего школьного возраста.
Естественно, я начала его проходить.. Результат 7 из 13. То ли на меня жара так действует и я чего-то недопонимаю, то ли у составителя кривые руки или мозги. Ну да, про дни недели я не поняла и "тыкнула" просто так. Но, например, к двум задачам я не нашла ответа в списках предложенных, брала наиболее близкие по величине. Хотелось бы, чтобы кто-нибудь проверил..
P.S. Если кто заинтересуется и будет проходить, то регистрироваться не надо, ответы составителя у меня есть.

@темы: Головоломки и занимательные задачи

---

[countess_lr]

Здравствуйте.
Застопорилась в контрольной по вышке (2 курс),
Посмотрите, плиз, решение. Срок до следующей пятницы (1.08.08)





Вроде как все должно быть верно, но что-то сомнения у меня возникают, особенно на счет первого примера.

Заранее спасибо.

@темы: Производная

---

Производная

[7XPEH7]

Есть функция

нужно найти её производную.
Даже и не знаю, как к ней подступиться, помогите, пожалуйста.

@темы: Производная

---

Производная

[7XPEH7]

Нужно найти производную от этой функции,

у меня получился такой ответ

в Mathcad получился другой ответ
.
Какой ответ правильный?

@темы: Производная

---

Живая Геометрия

[Robot]

Дорогие друзья!
Все, кто достаточно давно следит за нашим сообществом, наверное, заметили, что чертежи, выкладываемые мною к геометрическим задачам, отличаются от рисунков, сделанных в программах Paint, Word, Autocad и пр. Для создания рисунков я использую программу GeometrySketchpad (Живая Геометрия, сокращенно ЖГ). Ссылка на нее есть в эпиграфе (Раздел "Полезные программы"). В сообществе уже был небольшой пост на эту тему , написанный  #Free world#, но он был достаточно давно и, к сожалению, детального описания и небольшого хэлпа по работе с программой так и не последовало. Но сегодня наше сообщество нашел человек, который очень увлечен Живой Геометрией, создает эволюционные цепочки задач, для поиска решений которых используются динамические модели, построенные программой, иллюстрирует с помощью Живой Геометрии так называемый генетический прием. То есть в его руках ЖГ - это не просто программа-рисовалка, а настоящая Живая Геометрия.
Пишет  janka-x:

21.07.2008 в 12:26

Друзья!
Если интересуетесь Живой Геометрией, то заходите, пожалуйста, ко мне: janka-x.livejournal.com/
Пишите комменты. У меня там в последнее время по-белорусски. Но если вы напишите, то могу и на русский перейти.
Янка.

URL комментария

В его ЖЖ есть ссылки на ресурсы по этой программе ( в том числе и на уроки работы с ней), можно скачать ряд динамических моделей, методику описания работы с ЖГ и многое другое.
Его журнал будет полезен и тем, кто использует Живую Геометрию, и тем, кто хочет научиться работать с этой программой, и тем, кого просто увлекают исследовательские цепочки задач.

@темы: Ссылки, Полезные программы

---

все треугольники - равнобедренные :)

[Trotil]

Рассмотрим произвольный треугольник ABC и докажем, что AB = BC. Для этого проведём биссектрису угла B и серединный перпендикуляр к стороне AC. Пусть M | точка их пересечения. Опустим из точки M перпендикуляры MK и ML на стороны BA и BC. Точка M, лёжа на серединном перпендикуляре, одинаково отстоит от A и от C, то есть MA = MC. Находясь на биссектрисе угла B, она равноудалена от сторон этого угла, то есть MK = ML. Поэтому прямоугольные треугольники MKA и MLC равны по катету и гипотенузе. Значит, углы KAM и LCM, лежащие против равных катетов, тоже равны. Складывая эти углы с равными углами MAC и MCA (при основании равнобедренного треугольника AMC), получаем, что углы BAC и BCA равны, и треугольник равнобедренный.

Что не так в этом доказательстве?

---

C5 - вторая волна, привет

[devromik]

Выяснить, при каких значениях х, f ( f ( x ) ) = x;

f( x ) = 4 * 7^( x - 4 ) + 3, при х <= 5;
f( x ) = 3 * ( х - 3 ) / ( х - 4 ), при х > 5;

Решил его, думаю. По крайней мере f ( f ( x ) ) у меня действительно х, что хорошо. Решение выкладывать не буду, пока. Хочу посмотреть, кто и как бы его решил, если этот некто захочет, конечно.

@темы: ЕГЭ

---

Помогите пжалуйста!срочно нужно,до завтра

[Hot_Chili]

Основание прямой треугольной призмы - правильный треугольник ABC, сторона которого равна 8sqrt(3). На ребре BB1 отмечена точка P так, что BP:PB1=3:5. Найдите тангенс угла между плоскостями ABC и ACP, если расстояние между прямыми BC и A1C1 равно 16
___
у меня ответ с корнем получается...так запуталась,особенно в рисунке

@темы: Стереометрия, ЕГЭ

---

Ребят, помогите пожалуйста!!очень нужно!до завтра!

[Lira21]

1) Вычислить площадь фигуры, ограниченной линиями, уравнения которых y^2=2x+1 и x-y-1=0
2) Вычислить площадь фигуры, ограниченной параболами y^2+8x=16 и y^2-24x=48
3) Решить интеграл (xdx)/(koren(3x^2-11x+2))
4) Решить интеграл (koren(x) dx)/(koren(2x+3))
5) Вычислить длину дуги цепной линии y=a*ch(x/a) при этом x1=0, x2=b
6) Решить интеграл (x^3 dx)/(koren(x-1))

@темы: Приложения определенного интеграла, Интегралы

---

[Mumcryer]

Уважаемые знатоки, помогите пожалуйста решить несколько интегралов. Сдавать надо завтра, а голова вообще не варит.

1)
∫ 3х^2 + 8
x^3 + 4x^2 + 4x

2)

5
∫ xdx
0 √1+3x

3)

∫ √ (4 - x^2)^3
x^6

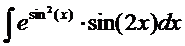
Заранее благодарю!

@темы: Интегралы

---

[Kristi13]

Здравствуйте, помогите с решение задач, пожалуйста

1. В прямоугольный треугольник с катетами длиной 3 и 4 впишите прямоугольник( с общим прямым углом) наибольшей площади. найти значение этой площади. (дано указание)
2. в прямоугольном треугольнике ABC угол C=90, угол A=30, M- середина AB, О- центр вписанной окружности. определить величину угла OMC. ( ответ 15 градусов) (дано указание)
3. в прямоугольной трапеции ABCD диагонали взаимно перпендикулярны, а отношение длин оснований AD:BC=3. найти отношение длин диагоналей. (дано указание)
4. равнобедренный треугольник с длинами сторон 8, 5 и 5 разделен на три равновеликие фигуры перпендикулярами, проведенными из некоторой точки к его сторонам. найдите расстояние от этой точки до каждой стороны данного треугольника
5. среди всех прямоугольников, вписанных в треугольник ABC со сторонами AB=5, BC=6, AC=7 таким образом, что две вершины прямоугольника лежат на стороне AC, а две другие на сторонах AB и BC соответственно, найдите прямоугольник с наибольшей площадью. вычислите значение этой наибольшей площади. (дано указание)
6. сумма синусов острых углов прямоугольного треугольника равна 15/корень из 3, а гипотенуза равна корень из 13. найдите расстояние от точки пересечения медиан треугольника до гипотенузы. (ошибка в условии)
7.дан угол а=30 с вершиной в точке О. На одной из сторон угла отмечены точки А и В, причем ОА=3 и ОВ<OA. На другой стороне угла отмечена точка М таким образом, что угол АМВ=90. Найдите наименьшее возможное значение длины АВ. (дано указание)
8. в трапеции ABCD основание AD=корень из 7. Диагонали AC и BD пересекаются в точке K, причем AK=1, KD=2, угол BAC=DAC. найти площадь трапеции ABCD.

Примечание Robot: Не получились пока 4 и 8

@темы: Планиметрия

---

[miss inconstancy]

помогите, пожалйста! пытаюсь разобраться, что есть двусторонняя поверхность и чем она отличасется от односторонней..
глава называется "многократные интегралы".

в лекции вот что написано..

не понимаю((
у меня еще приведены примеры: кольцо, лист мебиуса.. но надо как бы мысленно склеивать точки прямоугольника.. с кольцом еще понятно, а вот вторая что такое? может, у кого-нибудь есть картинки таких поверхностей?

@темы: Математический анализ

---

[Kristi13]

векторы AB=(-3;0;4) и AC=(5;-2;4) являются сторонами треугольника ABC. найти длину медианы AM

в трапеции ABCD отношение длины основания DC к длине основания AD равно n. диагонали трапеции пересекаются в точке О. Разложить вектор AO по векторам AB и AD

векторы p=a+3b и q=5a+3b перпендикулярны, при этом модуль а=модулю b и не равен 0. найдите угол между векторами a и b

векторы AB(3;-2;2) и BC(-1;0;-2) являются смежными сторонами параллелограмма. определите величину угла между диагоналями AC и BD

определить угол между векторами a+b и 2a-c, если a=-i+j-k, b=2i-j+2k, c=-2i+j-3k

огромное спасибо вам

@темы: Векторная алгебра