Я одна, но всё же я есть. Я не могу сделать всё, но всё же могу сделать что-то. И я не откажусь сделать то немногое, что могу (c)
Пробный ЕГЭ по математике (апрель 2011).
Еще несколько вариантов (часть С), найденных на просторах Инета, точнее, в большинстве своем на сайте и форуме Ларина А.А.
См. также страницу Пробный ЕГЭ по математике от 09 апреля 2011 года
Пробный ЕГЭ, Смоленск (пожалуй, это единственный пробник, которого у Ларина нет , из-за чего я начинаю опасаться, что он не совсем настоящий)
, из-за чего я начинаю опасаться, что он не совсем настоящий)
Целиком вариант
pr_04_2011_smolensk_1.jpg
pr_04_2011_smolensk_2.jpg
С1.
Решите уравнение
`(2sin^2x-cosx-2)log_(sinx)x^2=0`. Ответ: `1` , `(2pi)/3+2pik` , `k in Z`
C2.
В правильной треугольной пирамиде `SABC` с основанием `ABC` известны ребра `AB=sqrt(3)`, `SC=2sqrt(10)`. Найдите угол, образованный плоскостью основания и прямой `MN`, где `M`- середина ребра `AS`, а точка `N` делит ребро `BC` в отношении 1:2. Ответ: `arctg(3)`
С3
Решите неравенство:
`(log_2(3*2^(x-1)-1))/x >=1` Ответ: `x in (1-log_2 3;0) uu [1;+oo)`
C4
Сторона равностороннего треугольника `ABC` равна 10. Точка `D` лежит на прямой `BC` так что `BD C=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`. Ответ: 1 или 5.
C=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`. Ответ: 1 или 5.
Задача аналогична задаче с ЕГЭ2010 (западный вариант) eek.diary.ru/p112449326.htm
С5.
Найдите все значения `a`и `b` такие, что система имеет ровно два различных решения
`{(x^2+y^2-4x-6|y|+13-b^2 <=0),(y=ax-2sqrt(8)):}`. Ответ: `a=2sqrt(2), b = +-1`
C6
Перед каждым из чисел 10,11...,18 и 2,3,...,12 произвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 99 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Условия картинкой

Челябинск (14 апреля 2011)
Целиком вариант с форума Ларина alexlarin.com/download/file.php?id=1851
Ответы и критерии к нему alexlarin.com/download/file.php?id=1852
С1
Решите уравнение
`(6sin^2x-5cosx-5)/sqrt(sinx)=0`. Ответ: `x=arccos(1/6)+2pin, n in Z`
Условие картинкой
C2
В прямоугольном параллелепипеде `ABCDA_1B_1C_1D_1` найдите угол между прямой `A_1D` и плоскостью `BB_1D`, если `D D_1 =8, A_1D_1 =6 , D_1C_1=6`. Ответ: `arcsin((3sqrt(2))/10)`
C3
Решите неравенство `2*sqrt((1-4^x)/4^(x-1)) -63*sqrt(4^x/(1-4^x))<=3*sqrt(63)` Ответ: `x in [-3;0)`
Условие картинкой
C4
Угол между радиусом АО окружности, описанной около треугольника ABC и стороной АС равен 40°. Найдите угол А треугольника ABC, если угол С равен 30°.
Ответ: 20° или 100°
C5
Найдите все значения параметра `a`, при которых система уравнений
`{(log_yx=1),(x^2-3y+a=x):}`
имеет два решения. Ответ: `a in (0;3) uu (3;4)`
Условие картинкой
C6
Найдите все пары натуральных чисел а и b, удовлетворяющие
равенству `a^b+26 = bar(ba)` (в правой части стоит число, полученное дописыванием десятичной записи числа а после десятичной записи числа b) Ответ: `a=2, b = 4`
Условие картинкой
Челябинский вариант № 4
Целиком вариант www.egepro.ru/i/downloads/rege/math/4.pdf
Ответы и критерии к нему www.egepro.ru/i/downloads/rege/math/4_ans.pdf
С1 Решите уравнение
`(3cos^2x-sinx-1)/sqrt(cosx)=0`
C2 В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между прямой А1В и плоскостью АА1С, если АА1 =6, AB=8, ВС = 8.
C3 Решите неравенство
`4*sqrt((2^x-1)/2^x)+sqrt(14) <=14sqrt(2^(x-2)/(2^x-1)`
C4 Угол между радиусом АО окружности, описанной около треугольника AВС и стороной АС равен 45°. Найдите угол А треугольника ABC, если угол С равен 25°.
C5 Найдите все значения параметра а, при которых система уравнений
`{(y=e^(lnx)),(y=a+5x-x^2):}`
имеет два решения.
C6 Найдите все пары натуральных чисел а и b, удовлетворяющие равенству `a^b+8=bar(ab)`
Условия части С картинкой
Пробный ЕГЭ (12 апреля 2011 Санкт-Петербург)
Скачать варианты 1-2 с критериями и ответами с сайта Ларина: alexlarin.narod.ru/ege/2011/prob/spbprob.pdf
Вариант 1 (скачать целиком вариант с сайта Ларина А.А. alexlarin.narod.ru/ege/2011/prob/spb1.pdf)
С1. Решите уравнение
`(2sin^2x+2sinx*cos2x-1)/sqrt(cosx)=0`Ответ: `x=2pik +- pi/4, x=pi/6+2pin, k, n in Z`
C2. Длины всех ребер правильной четырехугольной пирамиды PABCD с вершиной Р равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка М — середина бокового ребра пирамиды АР.
Видеорешение от О.Себедаш
C3 Решите неравенство:
`(log_4(x^4-4x^3+4x^2)+log_(0,25)(6x^2-12x-9))/(x^2-2x-8)>=0` Ответ: `x in(-oo;-2) uu {-1;3} uu (4;+oo)`
С4. Четырехугольник ABCD описан около окружности и вписан в окружность. Прямые АВ и DC пересекаются в точке М . Найдите площадь четырехугольника, если известно, что`/_AMD=alpha` и радиусы окружностей, вписанных в треугольники ВМС и AMD равны соответственно г и R. Ответ: `S_(ABCD)=R/r (R^2-r^2 )ctg alpha/2` или `S_(ABCD)=r/R (r^2-R^2 )ctg alpha/2`.
С5. Найдите все значения параметра а, при каждом из которых система уравнений
`{(4|y-3|=12-3|x|),(y^2-a^2=3(2y-3)-x^2):} `
имеет ровно четыре решения. Ответ: `|a| in {12/5} uu (3;4)`.
С6. Найдите все такие простые числа р, для каждого из которых существует такое целое число k, что число р является общим
делителем чисел `k^4+12k^2+12` и `k^3+9k`. Ответ: `p in {2;3;5}`
Условия картинкой
Вариант 2 (скачать целиком вариант с сайта Ларина А.А. alexlarin.narod.ru/ege/2011/prob/spb2.pdf)
С1. Решите уравнение
`(2cos^2x+2cosx*cos2x-1)/sqrt(sinx)=0`
Видеорешение от О.Себедаш
C2. Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой. Найдите угол между прямыми PH и BM, если отрезок PH - высота данной пирамиды, а точка М — середина ее бокового ребра АР.
Видеорешение от О.Себедаш
C3. Решите неравенство:
`(log_(0,5)(8x^2+24x-16)+log_2(x^4+6x^3+9x^2))/(x^2+3x-10)>=0` Ответ: `x in(-oo;-5) uu {-4;1} uu (2;+oo)`
С4. Четырехугольник KLMN описан около окружности и вписан в окружность. Прямые KL и NM пересекаются в точке P . Найдите площадь треугольника KPN, если известно, что`/_KPN=phi` и радиусы окружностей, вписанных в треугольники KPN и LPM равны соответственно г и R.
С5. Найдите все значения параметра а, при каждом из которых система уравнений
`{(5|x+2|=60-12y),(4(x+1)+y^2=a^2-x^2):}`
имеет ровно восемь решений.
Видеорешение от О.Себедаш
С6. Найдите все такие простые числа р, для каждого из которых существует такое целое число k, что число р является общим
делителем чисел `k^4+15k^2+35` и `k^3+8k`. Ответ: `p in {3;5;7}`
Условия картинкой
Пробник из Казани (02.04.2011)
Целиком можно посмотреть: alexlarin.com/viewtopic.php?f=6&t=1266
С1
Решите уравнение
`(3cos^2x-5cosx+2)/sqrt(sinx)=0` Ответ: `x=arccos(2/3)+2pin`, `n in Z`.
C2
В правильной шестиугольной призме `ABCDEFA_1B_1C_1D_1E_1F_1` сторона основания равна 1, а высота равна 6. Найдите угол между прямой `F_1B_1` и плоскостью `AF_1C_1`.
Ответ: `arcsin((2sqrt(3))/7)`
C3
Решите неравенство
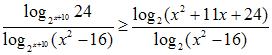 Ответ: `x in [-11;-10) uu (-10;-8) uu (4;sqrt(17))`
Ответ: `x in [-11;-10) uu (-10;-8) uu (4;sqrt(17))`
C4
В окружность радиуса `sqrt(10)` вписана трапеция с основаниями 2 и 4. Найдите расстояние от центра окружности до точки пересечения диагоналей трапеции. Ответ: `2 +-sqrt(6)/3`
C5
Для каждого значения `a > 0` найдите уравнения всех прямых, проходящих через начало координат и имеющих ровно две общие точки с графиком функции `f(x)=-x|x+8a|-16a^2`
C6
Найдите все пары натуральных чисел k и n таких, что `k < n` и `(n^2)^k=(k^2)^n`. Ответ: `k=2, n=4`
Условия картинкой
Калининградский пробник
alexlarin.com/viewtopic.php?f=6&t=1433
Вариант 3901
С1. Решите уравнение `log_(25-9x^2) (625-81x^4)=2+1/(log_3 (25-9x^2))
C2. В четырехугольнике ABCD длина стороны AB=12, синус угла BAC равен 0.32, синус угла ABD равен 0.48. Сумма углов BAD и BCD равна 180°. Найдите длину стороны BC.
C3. Решите неравенство `((-x+1)^(-1)-(-x+4)^(-1))^2 le (|x^2+6x|)/(x^2-5x+4)^2`
C4. В пирамиде FABC грани ABF и ABC перпендикулярны, FB:FA = 8:5. Тангенс угла между прямой BC и плоскостью ABF равен 5. Точка M выбрана на ребре BC так, что BM:МС = 3:5. Точка T лежит на прямой AF и равноудалена от точек M и B. Центр сферы, описанной около пирамиды FABC, лежит на ребре AB, площадь этой сферы равна `256pi`. Найдите объем пирамиды АВМТ.
C5. Найдите все значения параметра p, при каждом из которых уравнение `sqrt(4-3x)=x+2p(2-p)` имеет ровно р корней.
C6. Найдите все положительные значения a, при каждом из которых наименьшее из двух чисел `b=a^4(1-5a^(-2))-1` и `c = a^(-3)(5a-a^(-1))-1` больше -7.
Вариант 3902
С1. Решите уравнение `log_(2-x^2) (4-x^4)=1+1/(log_5 (2-x^2))+4log_25 5`
C2. К окружности провели две касательные МА и MB (А и В- точки касания). Найдите длину хорды АВ, если радиус окружности равен 20, а расстояние от точки М до хорды АВ равно 9.
C3. Решите неравенство `((x+1)^(-1)-(x+6)^(-1))^2 le (|x^2-10x|)/(x^2+7x+6)^2`
C4. Основанием пирамиды FABC является треугольник ABC, в котором AB=5, BC=12 и угол ABC=90°. Ребро AF перпендикулярно ABC и равно `2sqrt(4)`. Точки L и M расположены на ребрах FC и FB. При этом CL:FL=FL:FC, FM*MB = FB^2/9, причем точка M расположена ближе к B, чем к F. Найдите объем пирамиды AMLC.
C5. Пусть А - множество тех значений параметра а, для которых выполнено условие `x_1^3+x_2^3 le 27`, где `x_1` и `x_2` - действительные, различные корни уравнения `x^2-ax+3-a=0`. Найдите множество значений, которое при этих условиях принимает величина `x_1^2+x_2^2`.
C6. Найдите все положительные значения a, при каждом из которых наименьшее из двух чисел `b=a^4(1-5a^(-2))-1` и `c = a^(-3)(5a-a^(-1))-1` больше -7.
Дорогие учителя и школьники! Если у вас есть что-то, чем хотелось бы поделиться, будем очень рады. Заранее спасибо!!!
Еще несколько вариантов (часть С), найденных на просторах Инета, точнее, в большинстве своем на сайте и форуме Ларина А.А.
См. также страницу Пробный ЕГЭ по математике от 09 апреля 2011 года
Пробный ЕГЭ, Смоленск (пожалуй, это единственный пробник, которого у Ларина нет
 , из-за чего я начинаю опасаться, что он не совсем настоящий)
, из-за чего я начинаю опасаться, что он не совсем настоящий)Целиком вариант
pr_04_2011_smolensk_1.jpg
pr_04_2011_smolensk_2.jpg
С1.
Решите уравнение
`(2sin^2x-cosx-2)log_(sinx)x^2=0`. Ответ: `1` , `(2pi)/3+2pik` , `k in Z`
C2.
В правильной треугольной пирамиде `SABC` с основанием `ABC` известны ребра `AB=sqrt(3)`, `SC=2sqrt(10)`. Найдите угол, образованный плоскостью основания и прямой `MN`, где `M`- середина ребра `AS`, а точка `N` делит ребро `BC` в отношении 1:2. Ответ: `arctg(3)`
С3
Решите неравенство:
`(log_2(3*2^(x-1)-1))/x >=1` Ответ: `x in (1-log_2 3;0) uu [1;+oo)`
C4
Сторона равностороннего треугольника `ABC` равна 10. Точка `D` лежит на прямой `BC` так что `BD
 C=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`. Ответ: 1 или 5.
C=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`. Ответ: 1 или 5.Задача аналогична задаче с ЕГЭ2010 (западный вариант) eek.diary.ru/p112449326.htm
С5.
Найдите все значения `a`и `b` такие, что система имеет ровно два различных решения
`{(x^2+y^2-4x-6|y|+13-b^2 <=0),(y=ax-2sqrt(8)):}`. Ответ: `a=2sqrt(2), b = +-1`
C6
Перед каждым из чисел 10,11...,18 и 2,3,...,12 произвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 99 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Условия картинкой

Челябинск (14 апреля 2011)
Целиком вариант с форума Ларина alexlarin.com/download/file.php?id=1851
Ответы и критерии к нему alexlarin.com/download/file.php?id=1852
С1
Решите уравнение
`(6sin^2x-5cosx-5)/sqrt(sinx)=0`. Ответ: `x=arccos(1/6)+2pin, n in Z`
Условие картинкой
C2
В прямоугольном параллелепипеде `ABCDA_1B_1C_1D_1` найдите угол между прямой `A_1D` и плоскостью `BB_1D`, если `D D_1 =8, A_1D_1 =6 , D_1C_1=6`. Ответ: `arcsin((3sqrt(2))/10)`
C3
Решите неравенство `2*sqrt((1-4^x)/4^(x-1)) -63*sqrt(4^x/(1-4^x))<=3*sqrt(63)` Ответ: `x in [-3;0)`
Условие картинкой
C4
Угол между радиусом АО окружности, описанной около треугольника ABC и стороной АС равен 40°. Найдите угол А треугольника ABC, если угол С равен 30°.
Ответ: 20° или 100°
C5
Найдите все значения параметра `a`, при которых система уравнений
`{(log_yx=1),(x^2-3y+a=x):}`
имеет два решения. Ответ: `a in (0;3) uu (3;4)`
Условие картинкой
C6
Найдите все пары натуральных чисел а и b, удовлетворяющие
равенству `a^b+26 = bar(ba)` (в правой части стоит число, полученное дописыванием десятичной записи числа а после десятичной записи числа b) Ответ: `a=2, b = 4`
Условие картинкой
Челябинский вариант № 4
Целиком вариант www.egepro.ru/i/downloads/rege/math/4.pdf
Ответы и критерии к нему www.egepro.ru/i/downloads/rege/math/4_ans.pdf
С1 Решите уравнение
`(3cos^2x-sinx-1)/sqrt(cosx)=0`
C2 В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между прямой А1В и плоскостью АА1С, если АА1 =6, AB=8, ВС = 8.
C3 Решите неравенство
`4*sqrt((2^x-1)/2^x)+sqrt(14) <=14sqrt(2^(x-2)/(2^x-1)`
C4 Угол между радиусом АО окружности, описанной около треугольника AВС и стороной АС равен 45°. Найдите угол А треугольника ABC, если угол С равен 25°.
C5 Найдите все значения параметра а, при которых система уравнений
`{(y=e^(lnx)),(y=a+5x-x^2):}`
имеет два решения.
C6 Найдите все пары натуральных чисел а и b, удовлетворяющие равенству `a^b+8=bar(ab)`
Условия части С картинкой
Пробный ЕГЭ (12 апреля 2011 Санкт-Петербург)
Скачать варианты 1-2 с критериями и ответами с сайта Ларина: alexlarin.narod.ru/ege/2011/prob/spbprob.pdf
Вариант 1 (скачать целиком вариант с сайта Ларина А.А. alexlarin.narod.ru/ege/2011/prob/spb1.pdf)
С1. Решите уравнение
`(2sin^2x+2sinx*cos2x-1)/sqrt(cosx)=0`Ответ: `x=2pik +- pi/4, x=pi/6+2pin, k, n in Z`
C2. Длины всех ребер правильной четырехугольной пирамиды PABCD с вершиной Р равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка М — середина бокового ребра пирамиды АР.
Видеорешение от О.Себедаш
C3 Решите неравенство:
`(log_4(x^4-4x^3+4x^2)+log_(0,25)(6x^2-12x-9))/(x^2-2x-8)>=0` Ответ: `x in(-oo;-2) uu {-1;3} uu (4;+oo)`
С4. Четырехугольник ABCD описан около окружности и вписан в окружность. Прямые АВ и DC пересекаются в точке М . Найдите площадь четырехугольника, если известно, что`/_AMD=alpha` и радиусы окружностей, вписанных в треугольники ВМС и AMD равны соответственно г и R. Ответ: `S_(ABCD)=R/r (R^2-r^2 )ctg alpha/2` или `S_(ABCD)=r/R (r^2-R^2 )ctg alpha/2`.
С5. Найдите все значения параметра а, при каждом из которых система уравнений
`{(4|y-3|=12-3|x|),(y^2-a^2=3(2y-3)-x^2):} `
имеет ровно четыре решения. Ответ: `|a| in {12/5} uu (3;4)`.
С6. Найдите все такие простые числа р, для каждого из которых существует такое целое число k, что число р является общим
делителем чисел `k^4+12k^2+12` и `k^3+9k`. Ответ: `p in {2;3;5}`
Условия картинкой
Вариант 2 (скачать целиком вариант с сайта Ларина А.А. alexlarin.narod.ru/ege/2011/prob/spb2.pdf)
С1. Решите уравнение
`(2cos^2x+2cosx*cos2x-1)/sqrt(sinx)=0`
Видеорешение от О.Себедаш
C2. Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой. Найдите угол между прямыми PH и BM, если отрезок PH - высота данной пирамиды, а точка М — середина ее бокового ребра АР.
Видеорешение от О.Себедаш
C3. Решите неравенство:
`(log_(0,5)(8x^2+24x-16)+log_2(x^4+6x^3+9x^2))/(x^2+3x-10)>=0` Ответ: `x in(-oo;-5) uu {-4;1} uu (2;+oo)`
С4. Четырехугольник KLMN описан около окружности и вписан в окружность. Прямые KL и NM пересекаются в точке P . Найдите площадь треугольника KPN, если известно, что`/_KPN=phi` и радиусы окружностей, вписанных в треугольники KPN и LPM равны соответственно г и R.
С5. Найдите все значения параметра а, при каждом из которых система уравнений
`{(5|x+2|=60-12y),(4(x+1)+y^2=a^2-x^2):}`
имеет ровно восемь решений.
Видеорешение от О.Себедаш
С6. Найдите все такие простые числа р, для каждого из которых существует такое целое число k, что число р является общим
делителем чисел `k^4+15k^2+35` и `k^3+8k`. Ответ: `p in {3;5;7}`
Условия картинкой
Пробник из Казани (02.04.2011)
Целиком можно посмотреть: alexlarin.com/viewtopic.php?f=6&t=1266
С1
Решите уравнение
`(3cos^2x-5cosx+2)/sqrt(sinx)=0` Ответ: `x=arccos(2/3)+2pin`, `n in Z`.
C2
В правильной шестиугольной призме `ABCDEFA_1B_1C_1D_1E_1F_1` сторона основания равна 1, а высота равна 6. Найдите угол между прямой `F_1B_1` и плоскостью `AF_1C_1`.
Ответ: `arcsin((2sqrt(3))/7)`
C3
Решите неравенство
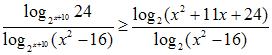 Ответ: `x in [-11;-10) uu (-10;-8) uu (4;sqrt(17))`
Ответ: `x in [-11;-10) uu (-10;-8) uu (4;sqrt(17))`C4
В окружность радиуса `sqrt(10)` вписана трапеция с основаниями 2 и 4. Найдите расстояние от центра окружности до точки пересечения диагоналей трапеции. Ответ: `2 +-sqrt(6)/3`
C5
Для каждого значения `a > 0` найдите уравнения всех прямых, проходящих через начало координат и имеющих ровно две общие точки с графиком функции `f(x)=-x|x+8a|-16a^2`
C6
Найдите все пары натуральных чисел k и n таких, что `k < n` и `(n^2)^k=(k^2)^n`. Ответ: `k=2, n=4`
Условия картинкой
Калининградский пробник
alexlarin.com/viewtopic.php?f=6&t=1433
Вариант 3901
С1. Решите уравнение `log_(25-9x^2) (625-81x^4)=2+1/(log_3 (25-9x^2))
C2. В четырехугольнике ABCD длина стороны AB=12, синус угла BAC равен 0.32, синус угла ABD равен 0.48. Сумма углов BAD и BCD равна 180°. Найдите длину стороны BC.
C3. Решите неравенство `((-x+1)^(-1)-(-x+4)^(-1))^2 le (|x^2+6x|)/(x^2-5x+4)^2`
C4. В пирамиде FABC грани ABF и ABC перпендикулярны, FB:FA = 8:5. Тангенс угла между прямой BC и плоскостью ABF равен 5. Точка M выбрана на ребре BC так, что BM:МС = 3:5. Точка T лежит на прямой AF и равноудалена от точек M и B. Центр сферы, описанной около пирамиды FABC, лежит на ребре AB, площадь этой сферы равна `256pi`. Найдите объем пирамиды АВМТ.
C5. Найдите все значения параметра p, при каждом из которых уравнение `sqrt(4-3x)=x+2p(2-p)` имеет ровно р корней.
C6. Найдите все положительные значения a, при каждом из которых наименьшее из двух чисел `b=a^4(1-5a^(-2))-1` и `c = a^(-3)(5a-a^(-1))-1` больше -7.
Вариант 3902
С1. Решите уравнение `log_(2-x^2) (4-x^4)=1+1/(log_5 (2-x^2))+4log_25 5`
C2. К окружности провели две касательные МА и MB (А и В- точки касания). Найдите длину хорды АВ, если радиус окружности равен 20, а расстояние от точки М до хорды АВ равно 9.
C3. Решите неравенство `((x+1)^(-1)-(x+6)^(-1))^2 le (|x^2-10x|)/(x^2+7x+6)^2`
C4. Основанием пирамиды FABC является треугольник ABC, в котором AB=5, BC=12 и угол ABC=90°. Ребро AF перпендикулярно ABC и равно `2sqrt(4)`. Точки L и M расположены на ребрах FC и FB. При этом CL:FL=FL:FC, FM*MB = FB^2/9, причем точка M расположена ближе к B, чем к F. Найдите объем пирамиды AMLC.
C5. Пусть А - множество тех значений параметра а, для которых выполнено условие `x_1^3+x_2^3 le 27`, где `x_1` и `x_2` - действительные, различные корни уравнения `x^2-ax+3-a=0`. Найдите множество значений, которое при этих условиях принимает величина `x_1^2+x_2^2`.
C6. Найдите все положительные значения a, при каждом из которых наименьшее из двух чисел `b=a^4(1-5a^(-2))-1` и `c = a^(-3)(5a-a^(-1))-1` больше -7.
Дорогие учителя и школьники! Если у вас есть что-то, чем хотелось бы поделиться, будем очень рады. Заранее спасибо!!!










-
-
15.04.2011 в 17:27-
-
15.04.2011 в 17:55Порешаем
-
-
15.04.2011 в 17:56-
-
15.04.2011 в 17:57Спасибо !!
-
-
15.04.2011 в 18:09Пробный ЕГЭ по математике от 09 апреля 2011 года
И если Вы знаете ответы к части В, то мы будем рады их выложить. Мне прорешивать часть В как-то неинтересно
-
-
15.04.2011 в 18:10Спасибо. Там пробелы по части С.
-
-
15.04.2011 в 18:13Мы просто ничего не успеваем=(
Если в сообществе задают вопрос по заданию, тогда стимул есть решать. А так... Ну, вот выложена часть решений - и что? кому это нужно?
-
-
15.04.2011 в 18:20Нужно
требовать оплатырекламировать пользу от размещения ответов и полных решений в таких топиках. Пришел, скажем, пятиклассник с каким-то мелким вопросом - помощь ему не нужно оказывать до тех пор, пока он не предоставит полное решение одного из заданий ЕГЭ. Бартер, так сказать.-
-
15.04.2011 в 18:25-
-
15.04.2011 в 18:32VEk
Спасибо. Можете не торопиться. Можно и утром в воскресение. И, вообще, когда и если будет настроение.
-
-
15.04.2011 в 18:52-
-
15.04.2011 в 18:53Можно и решения.
-
-
15.04.2011 в 18:54Умница!
Хорошо бы решения.
-
-
15.04.2011 в 19:22`(2sin^2x-cosx-2)*log_(sinx)(x^2)=0`
ОДЗ `{(x!=0),(sinx>0),(sinx!=1.):}`
1) `2sin^2x-cosx-2=0`
`2-2cos^2x-cosx-2=0`
`-cosx*(2cosx+1)=0`
`cosx=0` или `cosx=-1/2`
`x=pi/2+pin` - не удовл. ОДЗ
`x=(2pi)/3+2pik` - удовл. ОДЗ
`x=-(2pi)/3+2pik` - не удовл. ОДЗ
2) `log_(sinx)(x^2)=0`
`log_(sinx)(x^2)=log_(sinx)1`
`x^2=1`
`x=1` - удовл. ОДЗ, т.к. `sin1>0`
`x=-1` - не удовл. ОДЗ, т.к. `sin(-1)=-sin1<0`
Ответ: `1` , `(2pi)/3+2pik` , `k in Z`
-
-
15.04.2011 в 19:43Когда я вижу в С6 слова "перед каждым из чисел бла-бла-бла..." я сразу верю, что это настоящий пробник
У меня еще пять вариантов пробников надо их привести в приличный вид и выложить.
-
-
15.04.2011 в 20:15Очень хорошо.
На ЕГЭ чуть поподробнее надо, почему sin1 >0
aalleexx я сразу верю, что это настоящий пробник
-
-
15.04.2011 в 20:34`(log_2(3*2^(x-1)-1))/x>=1`
`(log_2(3*2^(x-1)-1)-x)/x>=0`
`(log_2(3*2^(x-1)-1)-log_2(2^x))/x>=0`
Рассмотрим функцию `f(x)=(log_2(3*2^(x-1)-1)-log_2(2^x))/x`
Найдем `D(f)`
`{(3*2^(x-1)-1>0),(x!=0):}`
1)`3/2*2^x>1`
`2^x>2/3`
`x>log_2(2/3)`
`log_2(2/3)<0`, т.к. `2/3<1`
`D(f)=(log_2(2/3);0)uuu(0;+oo)`
нули функции: `log_2(3*2^(x-1)-1)-log_2(2^x)=0`
`log_2(3*2^(x-1)-1)=log_2(2^x)`
`3*2^(x-1)-1=2^x`
`1,5*2^x-2^x=1`
`0,5*2^x=1`
`2^x=2`
`x=1`
Отмечаем на числовой прямой нули числителя, нули знаменателя и ОДЗ
читать дальше
Ответ: `(log_2(2/3);0)uuu[1;+oo)`
-
-
15.04.2011 в 20:44Robot так можно?
Функция `y=sinx` возрастает на `[-pi/2;pi/2]` , `0` и `1` принадлежат этому промежутку.
`1>0 => sin1>sin0=0`
-
-
15.04.2011 в 20:49-
-
15.04.2011 в 20:49-
-
15.04.2011 в 22:10Спасибо большое за С3
здесь в принципе методом рационализации еще можно было бы пользоваться.
А С2 можно просто как во время тренинга - картинкой.
Я ее потом перезалью в БИ сообщества
-
-
15.04.2011 в 22:53я этот метод не очень понимаю. Нам сказали что есть такой метод, но в чем он заключается мы не разбирали.
С2 сейчас попробую в граф. редакторе сделать, если не получится выложу скан своего решения.
-
-
16.04.2011 в 12:19-
-
16.04.2011 в 12:22чертеж
Основные пункты решения:
`AF`-высота в равностороннем треугольнике `AF=(asqrt3)/2=3/2`
`AO=2/3AF=1`
`SO=sqrt39` (из `DeltaASO` по теореме Пифагора)
`ME` - средняя линия в `DeltaASO`
`ME=1/2SO=sqrt39/2`
`BN=1/3BC=sqrt3/3`
`FN=1/2BC-BN=sqrt3/2-sqrt3/3=sqrt3/6`
`EN=sqrt(13/12)=sqrt13/(2sqrt3)` (из `DeltaEFN` по теореме Пифагора)
из `DeltaMEN` `tga=(ME)/(EN)=sqrt39/2
`a=arctg3`
Ответ: `arctg3`
-
-
16.04.2011 в 21:44Большое спасибо!!
Довольно замысловатая тут задача.
Bruks
Я не смотрела еще эти варианты.
Вот quest_ спасибо за решения.
Буду рада и решениям других задач.
-
-
17.04.2011 в 13:42Неверный
-
-
17.04.2011 в 14:22k^3+8k=k(k^2+8)
1. Пусть p - делитель k, тогда p - делитель 35. p = 5, p = 7
2. Пусть p - не равный 5 и 7 делитель k^2+8, тогда p - делитель k^4+15k^2+35-k(k^3+8k)=7k^2+35=7(k^2+5), следовательно, p - делитель k^2+5, следовательно, p - делитель k^2+8-(k^2+5)=3, следовательно, p = 3.
-
-
17.04.2011 в 15:31Вот в СПб очень хорошие видеорешения. Можно сделать такое и для этой задачи?
Кстати, СПб С2 вар2 я решала по другому, через тангенс и у меня получилось `arctgsqrt5`.
Это тоже самое, что и у Вас, я потом по формулам тригонометрии проверила, но через тангенс мне показалось проще.
-
-
17.04.2011 в 15:52Я тут ничего не делаю, только наблюдаю=)
Вот чертеж к С2 Казань
Задачу не решала, просто соображения по проведению перпендикуляра из точки `B_1` на плоскость `AF_1C_1`. Этот перпендикуляр будет лежать в плоскости, проходящей через `B_1` и перпендикулярной `AF_1C_1` Такой плоскостью будет `B B_1D_1 D`
Пусть плоскости пересекаются по прямой `BT`. Проводим `BK _|_ BT`
Доказываем, что `BK` будет перпендикуляром и к плоскости `AF_1C_1`
Далее останетс счет
-
-
17.04.2011 в 16:00В вариантах Спб по задаче C2 есть видеорешения, там ничего не подписывал.
А здесь, если не наврал в арифметике, `arcsin((2sqrt(3))/7)`.