`sqrt((x+1)/(x-3))*((x^2-7x+10)/((x-7)(x-5)))*sqrt((8-x)(x+4))<=0`
суббота, 16 апреля 2011
Хм, а как можно воспользоваться им в данной случае?
`sqrt((x+1)/(x-3))*((x^2-7x+10)/((x-7)(x-5)))*sqrt((8-x)(x+4))<=0`
`sqrt((x+1)/(x-3))*((x^2-7x+10)/((x-7)(x-5)))*sqrt((8-x)(x+4))<=0`
Если мысль не укладывается в голове, значит либо эта не та мысль, либо эта не та голова.
Пропустила пару и как-то потерялась... Подскажите как решать или где можно прочитать хорошо описано решение подобных задач:
1) Проверить будут ли следующие системы векторов полными в линейном пространстве R^3
а1=(0,-1,2),а2=(-3,2,2), а3=(-6,6,0), а4=(-9,7,4)
2)проверить является ли сисема векторов базисом в линейном пространстве R^3:
а1=(0,1,1), а2=(3,2,-1), а3=(-6,-5,1)
3)Проверить, является ли система векторов базисом в линейном пространстве R^3 и найти координаты вектора х в этом базисе. по известному вектору уе найти вектор у:
е1=(-3,-1,3),е2=(-3,-1,-4), е3=(3,2,-1), х=(6,5,-7), уе=(-2,0,1)
1) Проверить будут ли следующие системы векторов полными в линейном пространстве R^3
а1=(0,-1,2),а2=(-3,2,2), а3=(-6,6,0), а4=(-9,7,4)
2)проверить является ли сисема векторов базисом в линейном пространстве R^3:
а1=(0,1,1), а2=(3,2,-1), а3=(-6,-5,1)
3)Проверить, является ли система векторов базисом в линейном пространстве R^3 и найти координаты вектора х в этом базисе. по известному вектору уе найти вектор у:
е1=(-3,-1,3),е2=(-3,-1,-4), е3=(3,2,-1), х=(6,5,-7), уе=(-2,0,1)
Иногда я делаю ошибки, иногда несу чушь. Но вы должны различать.
Методические разработки заочной физико-технической школы МФТИ 2000-2010. Собрано в одном флаконе RAR. Некоторые пособия на сайте МФТИ публиковались давно и сейчас недоступны. Некоторые вообще не публиковались. Идентичные издания разных лет возможно совпадают. Проверить это реально только в процессе их использования. Найти можно на ifolder.ru/23000760 (23.07 Мб)
Зеркало ifile.it/laue62i/MIFI.rar
Зеркало ifile.it/laue62i/MIFI.rar
Здравствуйте. Помогите, пожалуйста с этой задачей..
Никак не решается.
Очень важно!
В циллиндр вписан параллелепипед. Большая сторона его основания равна а. Диагональ параллелепипеда составляет с плоскостью основания угол А(альфа), а с большей боковой гранью угол В(бета). Найти объем циллиндра.
читать дальше
Никак не решается.
Очень важно!
В циллиндр вписан параллелепипед. Большая сторона его основания равна а. Диагональ параллелепипеда составляет с плоскостью основания угол А(альфа), а с большей боковой гранью угол В(бета). Найти объем циллиндра.
читать дальше
пятница, 15 апреля 2011
Верно ли это?
Если локальный экстремум (минимум) у непрерывной функции нескольких (2-х) переменных в заданной области только один, это значит, что минимальное значение функция будет принимать именно в этой точке? Функция же нигде не "уходит вниз", раз экстремумов больше нет.
Наверняка это верно и, возможно, есть какая-нибудь по этому поводу теорема
Возьмите аналогичный случай с функцией одной переменной.
Если локальный экстремум (минимум) у непрерывной функции нескольких (2-х) переменных в заданной области только один, это значит, что минимальное значение функция будет принимать именно в этой точке? Функция же нигде не "уходит вниз", раз экстремумов больше нет.
Наверняка это верно и, возможно, есть какая-нибудь по этому поводу теорема
Возьмите аналогичный случай с функцией одной переменной.
найдите среднее арифметическое корней уравнения?
√(2x+8) – √(x+2) = 2
я возвожу в квадрат, но в итоге с ответом не сходится....
может Вы знаете как решать по-другому?
√(2x+8) – √(x+2) = 2
я возвожу в квадрат, но в итоге с ответом не сходится....
может Вы знаете как решать по-другому?
Многим известно, что выражения `|f|-|g|` и `f^2-g^2` имеют одинаковые знаки.
Аналогичные свойства существуют для логарифмов, степенных функций и т.д.
Вот,что в данный момент я подразумеваю под методом рационализации.
Вот неравенство:
`(3-x-sqrt(5-x^2))/(cos((2x-7)/4)-cos((x-5)/4))>=0`
мой учитель утверждает, что тут тоже можно рационализировать разность косинусов, ссылаясь на область определения и пр.
в действительности ОДЗ `-sqrt(5)<=x<=sqrt(5)`
Каким образом тут можно воспользоваться методом рационализации?
Аналогичные свойства существуют для логарифмов, степенных функций и т.д.
Вот,что в данный момент я подразумеваю под методом рационализации.
Вот неравенство:
`(3-x-sqrt(5-x^2))/(cos((2x-7)/4)-cos((x-5)/4))>=0`
мой учитель утверждает, что тут тоже можно рационализировать разность косинусов, ссылаясь на область определения и пр.
в действительности ОДЗ `-sqrt(5)<=x<=sqrt(5)`
Каким образом тут можно воспользоваться методом рационализации?
Пособие содержит: 30 равноценных вариантов; Методические рекомендации по проведению; Критерии оценивания.
Автор: А. Г. Мерзляк., В. Б. Полонский., Н.С. Прокопенко., М. С. Якир.
формат: Djvu
изд-во: Ранок
год издания: 2011

Автор: А. Г. Мерзляк., В. Б. Полонский., Н.С. Прокопенко., М. С. Якир.
формат: Djvu
изд-во: Ранок
год издания: 2011

Основание АД и ВС трапеции АВСД равны а и в (а больше в) . Найдите длину отрезка, который отрезается диагоналями трапеции на её средней линии.
Решить уравнение
` arctg(2sinx)=arc ctg(cosx) => x=pi/4+pin ; n in Z` а дальше не понятно ,почему они к совокупности сводили ?
читать дальше
` arctg(2sinx)=arc ctg(cosx) => x=pi/4+pin ; n in Z` а дальше не понятно ,почему они к совокупности сводили ?
читать дальше
В равнобедренной трапеции PRST (RS ||PT) проведена высота RA .Найдите длину отрезка AT ,если известно,что RS=7,PT=18.
Пытаюсь построить чертёж - не выходит.У меня получается,что RS и PT - диагонали,но они должны быть одинаковой длины,т.к трапеция равнобедренная.Разрешите дилемму ._.
Пытаюсь построить чертёж - не выходит.У меня получается,что RS и PT - диагонали,но они должны быть одинаковой длины,т.к трапеция равнобедренная.Разрешите дилемму ._.
Помогите пожалуйста решить С3
log_4(x^4 - 4x^3 + 4x^2) + log_0,25(6x^2 - 12x - 9) / x^2 - 2x - 8=0
Так, ОДЗ я описывать не буду, но получилось вот это:
(От -бесконечности; -2)(-2;3-sprt15/2)(3+sprt15/2;4)(4;+,бесконечности)
Дальше
log_4(x^4 - 4x^3 + 4x^2) + log_0,25(6x^2 - 12x - 9)=0
log_4(x^4 - 4x^3 + 4x^2) - log_4(6x^2 - 12x - 9)=0
log_4(x^4 - 4x^3 + 4x^2) = log_4(6x^2 - 12x - 9)
x^4 - 4x^3 + 4x^2 = 6x^2 - 12x - 9
x^4 - 4x^3 + 4x^2 - 6x^2 + 12x + 9=0
и тут у меня ступор, не знаю, что делать дальше(
log_4(x^4 - 4x^3 + 4x^2) + log_0,25(6x^2 - 12x - 9) / x^2 - 2x - 8=0
Так, ОДЗ я описывать не буду, но получилось вот это:
(От -бесконечности; -2)(-2;3-sprt15/2)(3+sprt15/2;4)(4;+,бесконечности)
Дальше
log_4(x^4 - 4x^3 + 4x^2) + log_0,25(6x^2 - 12x - 9)=0
log_4(x^4 - 4x^3 + 4x^2) - log_4(6x^2 - 12x - 9)=0
log_4(x^4 - 4x^3 + 4x^2) = log_4(6x^2 - 12x - 9)
x^4 - 4x^3 + 4x^2 = 6x^2 - 12x - 9
x^4 - 4x^3 + 4x^2 - 6x^2 + 12x + 9=0
и тут у меня ступор, не знаю, что делать дальше(
1.
Основание пирамиды- прямоугольный треугольник с катетами 6 и 8 см. Высота пирамиды равна 12 см и проходит через середину гипотенузы основания. Найдите площадь сечения пирамиды, проходящего через ее высоту и вершину прямого угла основания.
читать дальше
2.
Двугранный угол при основании правильной треугольной пирамиды равен 60 градусам. Найдите площадь боковой поверхности пирамиды, если расстояние от середины высоты пирамиды до ее апофемы равно 3 см.
3.
В правильной четырехугольной пирамиде двугранный угол при основании равен "альфа"ю Найдите площадь полной поверхности пирамиды, если ее высота равна Н.
читать дальше
Основание пирамиды- прямоугольный треугольник с катетами 6 и 8 см. Высота пирамиды равна 12 см и проходит через середину гипотенузы основания. Найдите площадь сечения пирамиды, проходящего через ее высоту и вершину прямого угла основания.
читать дальше
2.
Двугранный угол при основании правильной треугольной пирамиды равен 60 градусам. Найдите площадь боковой поверхности пирамиды, если расстояние от середины высоты пирамиды до ее апофемы равно 3 см.
3.
В правильной четырехугольной пирамиде двугранный угол при основании равен "альфа"ю Найдите площадь полной поверхности пирамиды, если ее высота равна Н.
читать дальше
Я одна, но всё же я есть. Я не могу сделать всё, но всё же могу сделать что-то. И я не откажусь сделать то немногое, что могу (c)
Пробный ЕГЭ по математике (апрель 2011).
Еще несколько вариантов (часть С), найденных на просторах Инета, точнее, в большинстве своем на сайте и форуме Ларина А.А.
См. также страницу Пробный ЕГЭ по математике от 09 апреля 2011 года
Пробный ЕГЭ, Смоленск (пожалуй, это единственный пробник, которого у Ларина нет , из-за чего я начинаю опасаться, что он не совсем настоящий)
, из-за чего я начинаю опасаться, что он не совсем настоящий)
Целиком вариант
pr_04_2011_smolensk_1.jpg
pr_04_2011_smolensk_2.jpg
С1.
Решите уравнение
`(2sin^2x-cosx-2)log_(sinx)x^2=0`. Ответ: `1` , `(2pi)/3+2pik` , `k in Z`
C2.
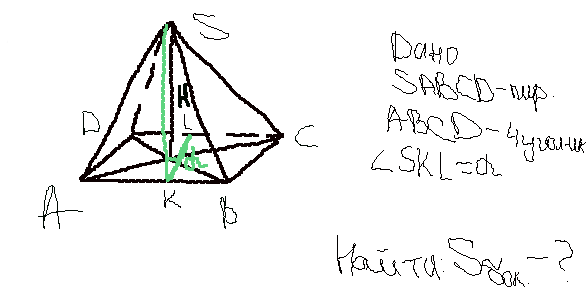
В правильной треугольной пирамиде `SABC` с основанием `ABC` известны ребра `AB=sqrt(3)`, `SC=2sqrt(10)`. Найдите угол, образованный плоскостью основания и прямой `MN`, где `M`- середина ребра `AS`, а точка `N` делит ребро `BC` в отношении 1:2. Ответ: `arctg(3)`
С3
Решите неравенство:
`(log_2(3*2^(x-1)-1))/x >=1` Ответ: `x in (1-log_2 3;0) uu [1;+oo)`
C4
Сторона равностороннего треугольника `ABC` равна 10. Точка `D` лежит на прямой `BC` так что `BD C=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`. Ответ: 1 или 5.
C=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`. Ответ: 1 или 5.
Задача аналогична задаче с ЕГЭ2010 (западный вариант) eek.diary.ru/p112449326.htm
С5.
Найдите все значения `a`и `b` такие, что система имеет ровно два различных решения
`{(x^2+y^2-4x-6|y|+13-b^2 <=0),(y=ax-2sqrt(8)):}`. Ответ: `a=2sqrt(2), b = +-1`
C6
Перед каждым из чисел 10,11...,18 и 2,3,...,12 произвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 99 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Условия картинкой

Челябинск (14 апреля 2011)
Целиком вариант с форума Ларина alexlarin.com/download/file.php?id=1851
Ответы и критерии к нему alexlarin.com/download/file.php?id=1852
С1
Решите уравнение
`(6sin^2x-5cosx-5)/sqrt(sinx)=0`. Ответ: `x=arccos(1/6)+2pin, n in Z`
Условие картинкой
C2
В прямоугольном параллелепипеде `ABCDA_1B_1C_1D_1` найдите угол между прямой `A_1D` и плоскостью `BB_1D`, если `D D_1 =8, A_1D_1 =6 , D_1C_1=6`. Ответ: `arcsin((3sqrt(2))/10)`
C3
Решите неравенство `2*sqrt((1-4^x)/4^(x-1)) -63*sqrt(4^x/(1-4^x))<=3*sqrt(63)` Ответ: `x in [-3;0)`
Условие картинкой
C4
Угол между радиусом АО окружности, описанной около треугольника ABC и стороной АС равен 40°. Найдите угол А треугольника ABC, если угол С равен 30°.
Ответ: 20° или 100°
C5
Найдите все значения параметра `a`, при которых система уравнений
`{(log_yx=1),(x^2-3y+a=x):}`
имеет два решения. Ответ: `a in (0;3) uu (3;4)`
Условие картинкой
C6
Найдите все пары натуральных чисел а и b, удовлетворяющие
равенству `a^b+26 = bar(ba)` (в правой части стоит число, полученное дописыванием десятичной записи числа а после десятичной записи числа b) Ответ: `a=2, b = 4`
Условие картинкой
Челябинский вариант № 4
Целиком вариант www.egepro.ru/i/downloads/rege/math/4.pdf
Ответы и критерии к нему www.egepro.ru/i/downloads/rege/math/4_ans.pdf
С1 Решите уравнение
`(3cos^2x-sinx-1)/sqrt(cosx)=0`
C2 В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между прямой А1В и плоскостью АА1С, если АА1 =6, AB=8, ВС = 8.
C3 Решите неравенство
`4*sqrt((2^x-1)/2^x)+sqrt(14) <=14sqrt(2^(x-2)/(2^x-1)`
C4 Угол между радиусом АО окружности, описанной около треугольника AВС и стороной АС равен 45°. Найдите угол А треугольника ABC, если угол С равен 25°.
C5 Найдите все значения параметра а, при которых система уравнений
`{(y=e^(lnx)),(y=a+5x-x^2):}`
имеет два решения.
C6 Найдите все пары натуральных чисел а и b, удовлетворяющие равенству `a^b+8=bar(ab)`
Условия части С картинкой
Пробный ЕГЭ (12 апреля 2011 Санкт-Петербург)
Скачать варианты 1-2 с критериями и ответами с сайта Ларина: alexlarin.narod.ru/ege/2011/prob/spbprob.pdf
Вариант 1 (скачать целиком вариант с сайта Ларина А.А. alexlarin.narod.ru/ege/2011/prob/spb1.pdf)
С1. Решите уравнение
`(2sin^2x+2sinx*cos2x-1)/sqrt(cosx)=0`Ответ: `x=2pik +- pi/4, x=pi/6+2pin, k, n in Z`
C2. Длины всех ребер правильной четырехугольной пирамиды PABCD с вершиной Р равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка М — середина бокового ребра пирамиды АР.
Видеорешение от О.Себедаш
C3 Решите неравенство:
`(log_4(x^4-4x^3+4x^2)+log_(0,25)(6x^2-12x-9))/(x^2-2x-8)>=0` Ответ: `x in(-oo;-2) uu {-1;3} uu (4;+oo)`
С4. Четырехугольник ABCD описан около окружности и вписан в окружность. Прямые АВ и DC пересекаются в точке М . Найдите площадь четырехугольника, если известно, что`/_AMD=alpha` и радиусы окружностей, вписанных в треугольники ВМС и AMD равны соответственно г и R. Ответ: `S_(ABCD)=R/r (R^2-r^2 )ctg alpha/2` или `S_(ABCD)=r/R (r^2-R^2 )ctg alpha/2`.
С5. Найдите все значения параметра а, при каждом из которых система уравнений
`{(4|y-3|=12-3|x|),(y^2-a^2=3(2y-3)-x^2):} `
имеет ровно четыре решения. Ответ: `|a| in {12/5} uu (3;4)`.
С6. Найдите все такие простые числа р, для каждого из которых существует такое целое число k, что число р является общим
делителем чисел `k^4+12k^2+12` и `k^3+9k`. Ответ: `p in {2;3;5}`
Условия картинкой
Вариант 2 (скачать целиком вариант с сайта Ларина А.А. alexlarin.narod.ru/ege/2011/prob/spb2.pdf)
С1. Решите уравнение
`(2cos^2x+2cosx*cos2x-1)/sqrt(sinx)=0`
Видеорешение от О.Себедаш
C2. Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой. Найдите угол между прямыми PH и BM, если отрезок PH - высота данной пирамиды, а точка М — середина ее бокового ребра АР.
Видеорешение от О.Себедаш
C3. Решите неравенство:
`(log_(0,5)(8x^2+24x-16)+log_2(x^4+6x^3+9x^2))/(x^2+3x-10)>=0` Ответ: `x in(-oo;-5) uu {-4;1} uu (2;+oo)`
С4. Четырехугольник KLMN описан около окружности и вписан в окружность. Прямые KL и NM пересекаются в точке P . Найдите площадь треугольника KPN, если известно, что`/_KPN=phi` и радиусы окружностей, вписанных в треугольники KPN и LPM равны соответственно г и R.
С5. Найдите все значения параметра а, при каждом из которых система уравнений
`{(5|x+2|=60-12y),(4(x+1)+y^2=a^2-x^2):}`
имеет ровно восемь решений.
Видеорешение от О.Себедаш
С6. Найдите все такие простые числа р, для каждого из которых существует такое целое число k, что число р является общим
делителем чисел `k^4+15k^2+35` и `k^3+8k`. Ответ: `p in {3;5;7}`
Условия картинкой
Пробник из Казани (02.04.2011)
Целиком можно посмотреть: alexlarin.com/viewtopic.php?f=6&t=1266
С1
Решите уравнение
`(3cos^2x-5cosx+2)/sqrt(sinx)=0` Ответ: `x=arccos(2/3)+2pin`, `n in Z`.
C2
В правильной шестиугольной призме `ABCDEFA_1B_1C_1D_1E_1F_1` сторона основания равна 1, а высота равна 6. Найдите угол между прямой `F_1B_1` и плоскостью `AF_1C_1`.
Ответ: `arcsin((2sqrt(3))/7)`
C3
Решите неравенство
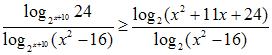 Ответ: `x in [-11;-10) uu (-10;-8) uu (4;sqrt(17))`
Ответ: `x in [-11;-10) uu (-10;-8) uu (4;sqrt(17))`
C4
В окружность радиуса `sqrt(10)` вписана трапеция с основаниями 2 и 4. Найдите расстояние от центра окружности до точки пересечения диагоналей трапеции. Ответ: `2 +-sqrt(6)/3`
C5
Для каждого значения `a > 0` найдите уравнения всех прямых, проходящих через начало координат и имеющих ровно две общие точки с графиком функции `f(x)=-x|x+8a|-16a^2`
C6
Найдите все пары натуральных чисел k и n таких, что `k < n` и `(n^2)^k=(k^2)^n`. Ответ: `k=2, n=4`
Условия картинкой
Калининградский пробник
alexlarin.com/viewtopic.php?f=6&t=1433
Вариант 3901
С1. Решите уравнение `log_(25-9x^2) (625-81x^4)=2+1/(log_3 (25-9x^2))
C2. В четырехугольнике ABCD длина стороны AB=12, синус угла BAC равен 0.32, синус угла ABD равен 0.48. Сумма углов BAD и BCD равна 180°. Найдите длину стороны BC.
C3. Решите неравенство `((-x+1)^(-1)-(-x+4)^(-1))^2 le (|x^2+6x|)/(x^2-5x+4)^2`
C4. В пирамиде FABC грани ABF и ABC перпендикулярны, FB:FA = 8:5. Тангенс угла между прямой BC и плоскостью ABF равен 5. Точка M выбрана на ребре BC так, что BM:МС = 3:5. Точка T лежит на прямой AF и равноудалена от точек M и B. Центр сферы, описанной около пирамиды FABC, лежит на ребре AB, площадь этой сферы равна `256pi`. Найдите объем пирамиды АВМТ.
C5. Найдите все значения параметра p, при каждом из которых уравнение `sqrt(4-3x)=x+2p(2-p)` имеет ровно р корней.
C6. Найдите все положительные значения a, при каждом из которых наименьшее из двух чисел `b=a^4(1-5a^(-2))-1` и `c = a^(-3)(5a-a^(-1))-1` больше -7.
Вариант 3902
С1. Решите уравнение `log_(2-x^2) (4-x^4)=1+1/(log_5 (2-x^2))+4log_25 5`
C2. К окружности провели две касательные МА и MB (А и В- точки касания). Найдите длину хорды АВ, если радиус окружности равен 20, а расстояние от точки М до хорды АВ равно 9.
C3. Решите неравенство `((x+1)^(-1)-(x+6)^(-1))^2 le (|x^2-10x|)/(x^2+7x+6)^2`
C4. Основанием пирамиды FABC является треугольник ABC, в котором AB=5, BC=12 и угол ABC=90°. Ребро AF перпендикулярно ABC и равно `2sqrt(4)`. Точки L и M расположены на ребрах FC и FB. При этом CL:FL=FL:FC, FM*MB = FB^2/9, причем точка M расположена ближе к B, чем к F. Найдите объем пирамиды AMLC.
C5. Пусть А - множество тех значений параметра а, для которых выполнено условие `x_1^3+x_2^3 le 27`, где `x_1` и `x_2` - действительные, различные корни уравнения `x^2-ax+3-a=0`. Найдите множество значений, которое при этих условиях принимает величина `x_1^2+x_2^2`.
C6. Найдите все положительные значения a, при каждом из которых наименьшее из двух чисел `b=a^4(1-5a^(-2))-1` и `c = a^(-3)(5a-a^(-1))-1` больше -7.
Дорогие учителя и школьники! Если у вас есть что-то, чем хотелось бы поделиться, будем очень рады. Заранее спасибо!!!
Еще несколько вариантов (часть С), найденных на просторах Инета, точнее, в большинстве своем на сайте и форуме Ларина А.А.
См. также страницу Пробный ЕГЭ по математике от 09 апреля 2011 года
Пробный ЕГЭ, Смоленск (пожалуй, это единственный пробник, которого у Ларина нет
 , из-за чего я начинаю опасаться, что он не совсем настоящий)
, из-за чего я начинаю опасаться, что он не совсем настоящий)Целиком вариант
pr_04_2011_smolensk_1.jpg
pr_04_2011_smolensk_2.jpg
С1.
Решите уравнение
`(2sin^2x-cosx-2)log_(sinx)x^2=0`. Ответ: `1` , `(2pi)/3+2pik` , `k in Z`
C2.
В правильной треугольной пирамиде `SABC` с основанием `ABC` известны ребра `AB=sqrt(3)`, `SC=2sqrt(10)`. Найдите угол, образованный плоскостью основания и прямой `MN`, где `M`- середина ребра `AS`, а точка `N` делит ребро `BC` в отношении 1:2. Ответ: `arctg(3)`
С3
Решите неравенство:
`(log_2(3*2^(x-1)-1))/x >=1` Ответ: `x in (1-log_2 3;0) uu [1;+oo)`
C4
Сторона равностороннего треугольника `ABC` равна 10. Точка `D` лежит на прямой `BC` так что `BD
 C=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`. Ответ: 1 или 5.
C=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`. Ответ: 1 или 5.Задача аналогична задаче с ЕГЭ2010 (западный вариант) eek.diary.ru/p112449326.htm
С5.
Найдите все значения `a`и `b` такие, что система имеет ровно два различных решения
`{(x^2+y^2-4x-6|y|+13-b^2 <=0),(y=ax-2sqrt(8)):}`. Ответ: `a=2sqrt(2), b = +-1`
C6
Перед каждым из чисел 10,11...,18 и 2,3,...,12 произвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 99 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Условия картинкой

Челябинск (14 апреля 2011)
Целиком вариант с форума Ларина alexlarin.com/download/file.php?id=1851
Ответы и критерии к нему alexlarin.com/download/file.php?id=1852
С1
Решите уравнение
`(6sin^2x-5cosx-5)/sqrt(sinx)=0`. Ответ: `x=arccos(1/6)+2pin, n in Z`
Условие картинкой
C2
В прямоугольном параллелепипеде `ABCDA_1B_1C_1D_1` найдите угол между прямой `A_1D` и плоскостью `BB_1D`, если `D D_1 =8, A_1D_1 =6 , D_1C_1=6`. Ответ: `arcsin((3sqrt(2))/10)`
C3
Решите неравенство `2*sqrt((1-4^x)/4^(x-1)) -63*sqrt(4^x/(1-4^x))<=3*sqrt(63)` Ответ: `x in [-3;0)`
Условие картинкой
C4
Угол между радиусом АО окружности, описанной около треугольника ABC и стороной АС равен 40°. Найдите угол А треугольника ABC, если угол С равен 30°.
Ответ: 20° или 100°
C5
Найдите все значения параметра `a`, при которых система уравнений
`{(log_yx=1),(x^2-3y+a=x):}`
имеет два решения. Ответ: `a in (0;3) uu (3;4)`
Условие картинкой
C6
Найдите все пары натуральных чисел а и b, удовлетворяющие
равенству `a^b+26 = bar(ba)` (в правой части стоит число, полученное дописыванием десятичной записи числа а после десятичной записи числа b) Ответ: `a=2, b = 4`
Условие картинкой
Челябинский вариант № 4
Целиком вариант www.egepro.ru/i/downloads/rege/math/4.pdf
Ответы и критерии к нему www.egepro.ru/i/downloads/rege/math/4_ans.pdf
С1 Решите уравнение
`(3cos^2x-sinx-1)/sqrt(cosx)=0`
C2 В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между прямой А1В и плоскостью АА1С, если АА1 =6, AB=8, ВС = 8.
C3 Решите неравенство
`4*sqrt((2^x-1)/2^x)+sqrt(14) <=14sqrt(2^(x-2)/(2^x-1)`
C4 Угол между радиусом АО окружности, описанной около треугольника AВС и стороной АС равен 45°. Найдите угол А треугольника ABC, если угол С равен 25°.
C5 Найдите все значения параметра а, при которых система уравнений
`{(y=e^(lnx)),(y=a+5x-x^2):}`
имеет два решения.
C6 Найдите все пары натуральных чисел а и b, удовлетворяющие равенству `a^b+8=bar(ab)`
Условия части С картинкой
Пробный ЕГЭ (12 апреля 2011 Санкт-Петербург)
Скачать варианты 1-2 с критериями и ответами с сайта Ларина: alexlarin.narod.ru/ege/2011/prob/spbprob.pdf
Вариант 1 (скачать целиком вариант с сайта Ларина А.А. alexlarin.narod.ru/ege/2011/prob/spb1.pdf)
С1. Решите уравнение
`(2sin^2x+2sinx*cos2x-1)/sqrt(cosx)=0`Ответ: `x=2pik +- pi/4, x=pi/6+2pin, k, n in Z`
C2. Длины всех ребер правильной четырехугольной пирамиды PABCD с вершиной Р равны между собой. Найдите угол между прямой BM и плоскостью BDP, если точка М — середина бокового ребра пирамиды АР.
Видеорешение от О.Себедаш
C3 Решите неравенство:
`(log_4(x^4-4x^3+4x^2)+log_(0,25)(6x^2-12x-9))/(x^2-2x-8)>=0` Ответ: `x in(-oo;-2) uu {-1;3} uu (4;+oo)`
С4. Четырехугольник ABCD описан около окружности и вписан в окружность. Прямые АВ и DC пересекаются в точке М . Найдите площадь четырехугольника, если известно, что`/_AMD=alpha` и радиусы окружностей, вписанных в треугольники ВМС и AMD равны соответственно г и R. Ответ: `S_(ABCD)=R/r (R^2-r^2 )ctg alpha/2` или `S_(ABCD)=r/R (r^2-R^2 )ctg alpha/2`.
С5. Найдите все значения параметра а, при каждом из которых система уравнений
`{(4|y-3|=12-3|x|),(y^2-a^2=3(2y-3)-x^2):} `
имеет ровно четыре решения. Ответ: `|a| in {12/5} uu (3;4)`.
С6. Найдите все такие простые числа р, для каждого из которых существует такое целое число k, что число р является общим
делителем чисел `k^4+12k^2+12` и `k^3+9k`. Ответ: `p in {2;3;5}`
Условия картинкой
Вариант 2 (скачать целиком вариант с сайта Ларина А.А. alexlarin.narod.ru/ege/2011/prob/spb2.pdf)
С1. Решите уравнение
`(2cos^2x+2cosx*cos2x-1)/sqrt(sinx)=0`
Видеорешение от О.Себедаш
C2. Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой. Найдите угол между прямыми PH и BM, если отрезок PH - высота данной пирамиды, а точка М — середина ее бокового ребра АР.
Видеорешение от О.Себедаш
C3. Решите неравенство:
`(log_(0,5)(8x^2+24x-16)+log_2(x^4+6x^3+9x^2))/(x^2+3x-10)>=0` Ответ: `x in(-oo;-5) uu {-4;1} uu (2;+oo)`
С4. Четырехугольник KLMN описан около окружности и вписан в окружность. Прямые KL и NM пересекаются в точке P . Найдите площадь треугольника KPN, если известно, что`/_KPN=phi` и радиусы окружностей, вписанных в треугольники KPN и LPM равны соответственно г и R.
С5. Найдите все значения параметра а, при каждом из которых система уравнений
`{(5|x+2|=60-12y),(4(x+1)+y^2=a^2-x^2):}`
имеет ровно восемь решений.
Видеорешение от О.Себедаш
С6. Найдите все такие простые числа р, для каждого из которых существует такое целое число k, что число р является общим
делителем чисел `k^4+15k^2+35` и `k^3+8k`. Ответ: `p in {3;5;7}`
Условия картинкой
Пробник из Казани (02.04.2011)
Целиком можно посмотреть: alexlarin.com/viewtopic.php?f=6&t=1266
С1
Решите уравнение
`(3cos^2x-5cosx+2)/sqrt(sinx)=0` Ответ: `x=arccos(2/3)+2pin`, `n in Z`.
C2
В правильной шестиугольной призме `ABCDEFA_1B_1C_1D_1E_1F_1` сторона основания равна 1, а высота равна 6. Найдите угол между прямой `F_1B_1` и плоскостью `AF_1C_1`.
Ответ: `arcsin((2sqrt(3))/7)`
C3
Решите неравенство
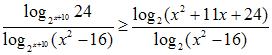 Ответ: `x in [-11;-10) uu (-10;-8) uu (4;sqrt(17))`
Ответ: `x in [-11;-10) uu (-10;-8) uu (4;sqrt(17))`C4
В окружность радиуса `sqrt(10)` вписана трапеция с основаниями 2 и 4. Найдите расстояние от центра окружности до точки пересечения диагоналей трапеции. Ответ: `2 +-sqrt(6)/3`
C5
Для каждого значения `a > 0` найдите уравнения всех прямых, проходящих через начало координат и имеющих ровно две общие точки с графиком функции `f(x)=-x|x+8a|-16a^2`
C6
Найдите все пары натуральных чисел k и n таких, что `k < n` и `(n^2)^k=(k^2)^n`. Ответ: `k=2, n=4`
Условия картинкой
Калининградский пробник
alexlarin.com/viewtopic.php?f=6&t=1433
Вариант 3901
С1. Решите уравнение `log_(25-9x^2) (625-81x^4)=2+1/(log_3 (25-9x^2))
C2. В четырехугольнике ABCD длина стороны AB=12, синус угла BAC равен 0.32, синус угла ABD равен 0.48. Сумма углов BAD и BCD равна 180°. Найдите длину стороны BC.
C3. Решите неравенство `((-x+1)^(-1)-(-x+4)^(-1))^2 le (|x^2+6x|)/(x^2-5x+4)^2`
C4. В пирамиде FABC грани ABF и ABC перпендикулярны, FB:FA = 8:5. Тангенс угла между прямой BC и плоскостью ABF равен 5. Точка M выбрана на ребре BC так, что BM:МС = 3:5. Точка T лежит на прямой AF и равноудалена от точек M и B. Центр сферы, описанной около пирамиды FABC, лежит на ребре AB, площадь этой сферы равна `256pi`. Найдите объем пирамиды АВМТ.
C5. Найдите все значения параметра p, при каждом из которых уравнение `sqrt(4-3x)=x+2p(2-p)` имеет ровно р корней.
C6. Найдите все положительные значения a, при каждом из которых наименьшее из двух чисел `b=a^4(1-5a^(-2))-1` и `c = a^(-3)(5a-a^(-1))-1` больше -7.
Вариант 3902
С1. Решите уравнение `log_(2-x^2) (4-x^4)=1+1/(log_5 (2-x^2))+4log_25 5`
C2. К окружности провели две касательные МА и MB (А и В- точки касания). Найдите длину хорды АВ, если радиус окружности равен 20, а расстояние от точки М до хорды АВ равно 9.
C3. Решите неравенство `((x+1)^(-1)-(x+6)^(-1))^2 le (|x^2-10x|)/(x^2+7x+6)^2`
C4. Основанием пирамиды FABC является треугольник ABC, в котором AB=5, BC=12 и угол ABC=90°. Ребро AF перпендикулярно ABC и равно `2sqrt(4)`. Точки L и M расположены на ребрах FC и FB. При этом CL:FL=FL:FC, FM*MB = FB^2/9, причем точка M расположена ближе к B, чем к F. Найдите объем пирамиды AMLC.
C5. Пусть А - множество тех значений параметра а, для которых выполнено условие `x_1^3+x_2^3 le 27`, где `x_1` и `x_2` - действительные, различные корни уравнения `x^2-ax+3-a=0`. Найдите множество значений, которое при этих условиях принимает величина `x_1^2+x_2^2`.
C6. Найдите все положительные значения a, при каждом из которых наименьшее из двух чисел `b=a^4(1-5a^(-2))-1` и `c = a^(-3)(5a-a^(-1))-1` больше -7.
Дорогие учителя и школьники! Если у вас есть что-то, чем хотелось бы поделиться, будем очень рады. Заранее спасибо!!!
Как решить систему ?
` sinx=0 ` `x=pin`
`sin^2x=1` ` x=+-pi/2+2pin `
` cosx=0` ` x=pi/2+pik `
`cos^2x=1 ` `x=2piz ; x=pi+2pin `
читать дальше
` sinx=0 ` `x=pin`
`sin^2x=1` ` x=+-pi/2+2pin `
` cosx=0` ` x=pi/2+pik `
`cos^2x=1 ` `x=2piz ; x=pi+2pin `
читать дальше
` (sinx)^2-(cosx)^2=0 `
`1)cos2x=0 =>2x=pi/2+pi*n => x=pi/4+pi*n/2`
`2) (sinx-cosx)(sinx+cosx)=0 => x= +- pi/4+pi*n `
Почему ответы не совпадают , или это тоже самое ?
Заранее Спасибо.
`1)cos2x=0 =>2x=pi/2+pi*n => x=pi/4+pi*n/2`
`2) (sinx-cosx)(sinx+cosx)=0 => x= +- pi/4+pi*n `
Почему ответы не совпадают , или это тоже самое ?
Заранее Спасибо.
Окружность описана около равностороннего треугольника АВС. На дуге ВС, не содержащей точку А, расположена точка М, делящая градусную меру этой дуги в отношении 1:2 .Найдите углы треугольника АМВ.
Помогите пожалуйста с задачей, мучаюсь, не могу решить.
Помогите пожалуйста с задачей, мучаюсь, не могу решить.
Сред.арифм трех чисел 6.Найдите эти числа,если первое число в 2,5 раза больше,а второе в 1,5 раза больше третьего