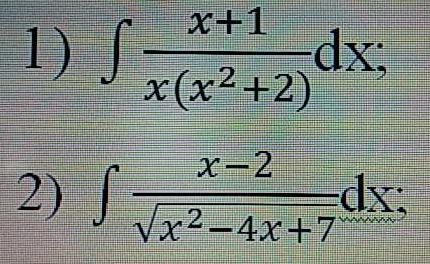[kirillka1992]

помогите найти границы интегрирования для системы `x=2*cos(t)^3` | `y=sin(t)^3
и подскажите каким способом можно найти `int x*(x-3)^3 dx`

@темы: Интегралы

---

Решить уравнение

[yonkis]

`((|x-5|)/3)+|x|=3`

@темы: Уравнения (неравенства) с модулем, ГИА (9 класс)

---

Здравствуйте!

[vanga]

В равнобедренной трапеции меньшее основание равно боковой стороне, большее основание равно 10 см., а угол при основании равен 70 градусов. Найдите периметр трапеции.

p.s. подскажите, какая тема?

@темы: Планиметрия

---

помогите

[наталья1011]

при каких значениях а сумма выражений log_a(sinx+2) и log_a(sinx+3) будет равна 1 хотя бы при одном значении х.

@темы: Задачи с параметром, ЕГЭ

---

Прогрессия

[yonkis]

Найдите все возможные значения переменной n, при которых сумма Sn некоторого количества последовательных нечетных чисел, начиная с 3, находятся в пределах от 675 до 960 включительно.

@темы: Прогрессии, ГИА (9 класс)

---

[вейко]

дано уравнение кривой x^6=4*(x^4-y^4)
найти уравнение кривой в полярных координатах,провел замену x=r*cos(a) ;y=r*sin(a)
получил r=2*cos(2a)/(cos(a))^3 не сходится с ответом

@темы: Аналитическая геометрия

---

найти производную dy/dx

[sobesednik]

y=arcsin(sqrt(1-3x)) y'=(1/sqrt(-3x))*(-3x)'=-3/sqrt(-3x) Верно ли решение?

@темы: Производная

---

[dos_ataka]

Сторона равностороннего треугольника `ABC` равна 10. Точка `D` лежит на прямой `BC` так что `BD : DC=2:3`. Окружности, вписанные в каждый из треугольников `ADC` и `ADB` касаются прямой `BC` в точках Е и F соответственно. Найти длину отрезка `EF`

@темы: Планиметрия

---

Помогите решить интеграл!!!

[RSI]

Заранее огромное спасибо!

1) ∫(x+1)/(x(x^2+2))dx;
2) ∫(x-2)/√(x^2-4x-7)dx;
условие картинкой

@темы: Интегралы

---

я правильно думаю?

[наталья1011]

при каких значениях а сумма выражений `log_a(sinx+2)` и `log_a(sinx+3)` будет равна `1` хотя бы при одном значении х.
свести к квадратному уравнению и рассмотреть три случая, чтобы корни принадлежали отрезку от -1 до 1.
тогда почему хотя бы при одном значении х ведь имеем дело с sinx

@темы: Задачи с параметром, ЕГЭ

---

Длина дуги

[atlant-e]

`x=cos^4t`
`y=sin^4t`
1) Почему что бы посчитать длину дуги в первой четверти мы берем интеграл от `0` до `pi/2` а не наоборот? Ведь `x=0` отвечает `t=pi/2`
2) И как, собственно, взять `int_0^(pi/2) sqrt(cos^6t*sin^2t+sin^6t*cos^2t) dt` ? Заменой `tant=u` Прихожу к `int u/(1+u^2)^3*sqrt(u^4+1) du`, что, кажется, еще хуже.

@темы: Приложения определенного интеграла

---

[Faith Lehane]

Здравствуйте! Помогите пожалуйста решить задачи

1. Найти площади плоских фигур, ограниченных линиями:
а) y^3-y=x, y=-(4+x)^2, y=0, y=-1
б) x=3t^2, y=3t-t^3, t принадлежит [0;1]

2. Вычислить объемы тел, образованных вращением вокруг оси и плоских фигур, ограниченных линиями:
y=x^3, y=4x, вокруг оси Oy

3. Найти площадь поверхности, образованной при вращении вокруг оси Ox кривых:
y=lncosx, x принадлежит [0;п/6]

Заранее благодарна

@темы: Приложения определенного интеграла

---

Геометрия

[kleopatra2782]

Основание пирамиды ТАВСД-прямоугольник АВСД.Ребро АТ перпендикулярно плоскости основания,грань ВСТ образует с плоскостью основания двугранный угол 30 градусов.Найдите площадь боковой поверхности пирамиды,если АТ=3м,ДТ=5м.

@темы: Стереометрия

---

Найти производные dy/dx

[sobesednik]

y=1/(tg^2(2x)) проверьте ответ

@темы: Производная

---

Найти наибольший общий делитель выражений 1/(a^-2-b^-2) и 1/(a^-3-b^-3)

[yonkis]

1) ab/b-a
2)a²b²/a-b
3)a²b²/b-a
4)a²b²/b²-a²

@темы: ГИА (9 класс)

---

производная y=x*sqrt((1+x^2)/(1-x))

[sobesednik]

Помогите с решением

`y=x*sqrt((1+x^2)/(1-x))`

@темы: Производная

---

Задача 9 класс

[yonkis]

Часовая и минутная стрелки часов находятся в таком положении что угол между ними равен 180˚. Через какое время минутная стрелка догонит часовую?

@темы: Олимпиадные задачи, ГИА (9 класс)

---

задачка с параметром

[наталья1011]

Найдите все значения а, при каждом из которых наибольшее значение функции `f(x)=x^2-7|x-a|-3x`на отрезке [-6; 6] принимается хотя бы на одном из концов этого отрезка.

@темы: Задачи с параметром, ЕГЭ

---

Задание с параметром

[yonkis]

При каких значениях параметра а парабола y=2ax²+(6a-1)x+4,5a-2 целиком располагается в нижней полуплоскости?

@темы: Задачи с параметром

---

геометрия

[kleopatra2782]

С1
Осевое сечение конуса - треугольник с углом 120 градусов. Радиус основания равен 3. Найдите площадь сечения, проходящего через две образующие, угол между которыми равен 45 градусам.

С2
Найдите расстояние от вершины С прямоугольного параллепипеда АВСДА1В1С1Д1 до диагонали ВД1, если СС1= `sqrt(11)`, ВС=3, СД=4

@темы: ЕГЭ