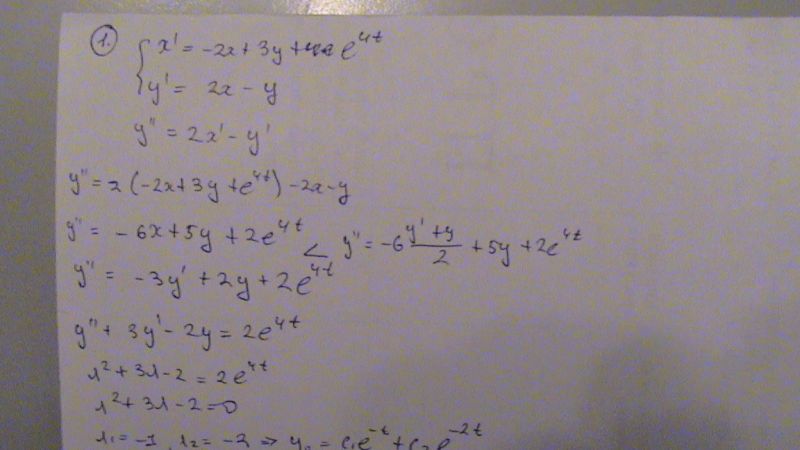Правильно?

[dana-beisalieva]

Один из углов прямоуголной трапеции равен 120 градусов, большее основание равно 12. Найдите отрезок, соединяющий середины диагоналей, если известно, что меньшая диагональ трапеции равна её большему основанию.



`angle ABC=120^@`
`DC=BD=12`
KL=?
`/_ BCD=60^@`
`Delta DBC`- равносторонний
`/_ BDC=/_ ABD=60^@`
`/_ADB=30^@`
`AB=1/2 BD=6
Далее я предположила по рисунку что KL лежит на средней линии, и что `KL=1/3 OF`
`OF=(AB+DC)/2=9`
`KL=1/3 OF=1/3 *9=3`
Если у меня правильно, то как доказать что KL лежит на средней линии?

@темы: Планиметрия

---

Помогите, пожалуйста. Срочно надо..

[Nic94]

Каким количеством способов можно вытащить из колоды 36 карт неупорядоченный набор из 6 карт, чтобы там обязательно были два короля и три червы.

Пожалуйста помогите очень надо))

@темы: Комбинаторика

---

Помогите....

[Nic94]

Сколькими способами из колоды карт в 36 листов можно брать неупорядоченный набор из 5 карт так, чтобы в этом наборе было бы точно: 2 чёрных карты, 1 карта червей, 1 туз.

Помогите решить, плиз)))

@темы: Комбинаторика

---

Помогите, пожалуйста

[Aslador]

Всем доброго времени суток. У меня возникли проблемы с решением (даже не столько решением, сколько доказательством) ряда.

По заданию дан был ряд: `sum_(1)^(oo) (3^n/(n*(x^2-2x+3)^n))`

Примем `x^2-2x+3` как `z`

`sum_(1)^(oo) (3^n/(n*z^n))`

У меня ошибка в определении такого `z`, при которой ряд сходится. Помогите пожалуйста решить эту проблему.

@темы: Ряды

---

[Emelli]

Помогите пожалуйста решить задачу!!! Через концы отрезка АВ и его середину О проведено параллельные прямые пересекающие некоторую плоскость в точках А1, В1, О1.знайдить длину отрезка ОО1, если АВ не пересекает плоскость, и АА1 = 8,3 ВВ1 = 4,1.

@темы: Прямая и плоскость в пространстве, Планиметрия

---

Задачка

[Nicas]

Найти размеры прямоугольника с наибольшей площадью,вписанного в прямоугольный треугольник,катеты которого,а=8 см и b=16см,а один из углов прямоугольника совпадает с прямым углом треугольника.

@темы: Задачи на экстремум, Производная

---

[sonja-kot]

sqrt(6-10cosx-sinx)<sinx-cosx
Решала систему: 1)правая часть >0
2)подкоренное >=0
3)6-10cosx-sin<1-sin2x
В 1)получ-сь 2pi*n+pi/4<x<2pi*n+5pi/4
В 3): (5-sinx)(1-2cosx)<0, т.е. х принадлежит (2pi*n-pi/3;2pi*n+pi/3)
И 1)+3): х принад-т (2pi*n+pi/4;2pi*n+pi/3)
А вот со вторым что делать?

@темы: Тригонометрия

---

Найти все идеалы Z

[...Полярная Звезда...]

Я не знаю даже как записать это. Я до этого решала, находила макс идеалы. Попробую оттолкнуться от этого
Правильно?
0={0}, (1)=(2)=...=(n)

---

[sonja-kot]

Добрый вечер,хочу узнать правильный ответ я получила,решая |2sinx-8cosx|=3sinx+8cosx
Понятно,что ОДЗ-это правая часть>=0,т.е.tgx>=-8/3 и х
а дальше решаем 1й случай модуль просто опускается и тогда: sinx=-16cosx я разделила обе части ур-я на cosx,т.к. он не может равняться 0 и получ-м х=-arctg16+pn
2й случай,когда открываем модуль с минусом и получаем х=pn
В ответ записываем х=p+pn и -arctg16+2pn

@темы: Тригонометрия

---

Область сходимости интегралов.

[Nick Martel]

Здравствуйте. Помогите, пожалуйста, с решением задачи.

Определить область сходимости интеграла:
`int_0^(+oo) ((sinx^q)/x^p)dx`
Попытки решения:
Замена `x^q=t`, тогда получаем:
`1/q int_0^(+oo) ((sint)/t^((p+1)/q))dt`
Пробую через признак Дирихле сходимости несобственных интегралов. `f(x)=sint, g(x)=1/t^((p+1)/q)`
1. `|int_0^b sint dt| = |-cost |_0^b |<= 2`
2. `d/dx (1/t^((p+1)/q))=-(p+1)/q1/t^((1-q+p)/q)`
Вопрос: как здесь определить знак?

@темы: Несобственные интегралы

---

[0xFAU]

Здравствуйте, помогите решить данное дифференциальное уравнение
(1-ln(t))*y''+y'/t-y/t^2=(1-ln(t))^2

Пробовала привести к уравнению Эйлера, но либо замены не те, либо неправильные дальнейшие подстановки
Заранее спасибо

@темы: Дифференциальные уравнения

---

[helen finch]

нужно найти нули функции, точки разрыва, производные, вторые производные, из за корня 3 степени впадаю в ступор...
`y=x/root(3)(x^2-1)` `y'=(root(3)(x^2-1)-(1/3)*x*root(3)((x^2-1)^-2))/root(3)((x^2-1)^2)` с нулями, разрывами, второй производной непонятки
`y=e^(2*x-x^2)` `y'=(2-2x)*e^(2*x-x^2)` с остальным та же проблема..
помогите пожалуйста

@темы: Исследование функций

---

[[email protected]]

Здравствуйте, пожалуйста, помогите решить задачку.

Составить уравнение прямой, проходящей через вершину параболы y=x^2-4x+7 и через точку А (-1;0). Сделать чертеж.

Спасибо.

@темы: Аналитическая геометрия

---

Отрицательная дисперсия

[fingerling6875]

Здравствуйте. Дана задача.

задача

Случайная величина Х задана функцией распределение:
`F(x)=`
`0`, при `x<=-pi/4`
`a*(cos(5x))^2`, при `-pi/4``<``x``<=``pi/3`
`1`, при `x>pi/3`

Найти среднеквадратическое отклонение `sigma(x)`

Как я решал

Найдем плотность (это первая производная от функции распределения):
`f(x)=`
`0`, при `x<=-pi/4`
`-5*a*sin(10x)`, при `-pi/4``<``x``<=``pi/3`
`0`, при `x>pi/3`

Найдем неизвестную a из уравнения:
`int_(-infty)^(-pi/4) 0*dx`+`int_(-pi/4)^(pi/3) (-5*a*sin(10x))*dx`+`int_(pi/3)^(+infty) 0*dx``=1`

`a=1/(int_(-pi/4)^(pi/3) (-5*sin(10x))*dx)=1/(-1/4)=-4`

Перепишем f(x)
`f(x)=`
`0`, при `x<=-pi/4`
`20sin(10x)`, при `-pi/4``<``x``<=``pi/3`
`0`, при `x>pi/3`

Найдем M(x) используя
`int_a^b x*f(x)*dx`
`M(x)=int_(-pi/4)^(pi/3) (20xsin(10x))*dx=pi/3-sqrt(3)/10+1/5=1,0739`

Найдем дисперсию по формуле:
`D(x)=int_a^b x^2*f(x)*dx-(M(x))^2`
`D(x)+(M(x))^2=int_(-pi/4)^(pi/3) (20x^2sin(10x))*dx=(1/25-2*x^2)*cos(10x)+2x*sin(10x)/5=0,3997`

`D(x)=0,3997-(1,0739)^2=-0,7536`

Все вычисления я делал на листике и проверял на wolframalpha.com


Укажите, пожалуйста, ошибки. Спасибо.

@темы: Теория вероятностей, Математическая статистика

---

Формула Тейлора

[Arcan]

`sqrt(e^(x^2)-1)` в точке `a=0` с точностью `n=6`
Разложил сначала то, что под корнем, вынес x^2, получил |x|.Этот модкль остается до последнего перехода и получается такой ответ: `|x|+|x|^3 /4 +5|x|^5 /96 +o(x^6)` Преподаватель просит доказать, что у функции нет разложения в формулу Тейлора. Помогите!

Как из моего ответа сделать вывод, что формулы Тейлора для этой функции не существует?

@темы: Математический анализ

---

Системы диффур

[Afu-Ra]

Здравствуйте, проверьте пожалуйста одну задачку

1. Решить систему дифференциальных уравнений `{(x'=-2x+3y+e^(4t)), (y'=2x-y):}`

Решение

.

@темы: Дифференциальные уравнения

---

Неравенства, 5 заданий

[Sunline1990]

Здравствуйте! Есть такие задания:
16.8 `((x-3)^2(5x+2)(x+3))/((x-1)(x+4)^2) > =0`
17.8 `|2x-1|/(x^2+x-2)>=3`
18.8 `sqrt(3x^2-2x-1)<x-1`
19.8 `(x^2-6x+8)*sqrt(100-21x-x^2)<=0`
20.8 `3*sqrt(x+3)-sqrt(x-2)>=7`

Мои решения

16.8 и 17.8

i078.radikal.ru/1212/1c/019a55957deb.jpg

18.8 и 19.8

s08.radikal.ru/i181/1212/28/b2d5360f2b2a.jpg

20.8

i051.radikal.ru/1212/c0/9dbf0a25c9ec.jpg

Прошу проверить, и, если неправильно что-то, исправить. Заранее спасибо!

@темы: Комбинированные уравнения и неравенства, Уравнения (неравенства) с модулем, Иррациональные уравнения (неравенства)

---

сходимость ряда

[jemma_84]

здравствуйте!
нужно исследовать на сходимость ряд `sum_{n= 2}^infty (ln n)^5/n^5` .вот как-то не могу придумать, с каким бы его рядом сравнить.....подскажите,пожалуйста.заранее спасибо

@темы: Ряды

---

Логнормальное распределение

[lubov_R]

В базисном периоде логнормальное распределение работающих по величине заработной платы характеризуется параметрами lnХср=4,518, G(сигма)=0,306, Xmin=50 (руб) Xmax=240 (руб). рассчитать прогнозируемые математическое ожидание и среднее квадратическое отклонение логарифмов заработной платы при следующих значениях проектируемого минимума и максимума заработной платы X'=70, X'=240

@темы: Математика в экономике, Математическая статистика

---

Конформные отображения.

[t.s.a.t.s]

Здравствуйте! Не могу решить задачи:
1) Конформно отобразить на верхнюю полуплоскость(или единичный круг, без разницы) область D = {|z|<1, |z+2i+1|<2, |z+2i-1|<2}
2) Отобразить на верхнюю полуплоскость, используя принцип симметрии, плоскость с разрезами по дугам окружностей |z|=1, |z-sqrt(2)|=1, лежащими в верхней полуплоскости.

В Первом делаю дробно-линейное отображение (z-1)/(z+1) и сдвигаю вниз на единицу. Получается четверть эллипса с фокусами в +-1, вроде можно применить ф-цию обратной ф-ции жуковского, там получится четверть кольца, а дальше, что делать не знаю.
Помогите, пожалуйста! Заранее спасибо.
Задание нужно сделать до завтра, 6 утра по Москве.

@темы: Математический анализ, Комплексные числа