[ДОБРЫЙВЕЧЕР]

Дана правильная 6-угольная пирамида с основанием = 1 и боковым ребром = 2. Найти угол между AL и BM, где L и M - середины ребер SB и SC соответственно.

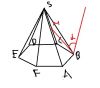
Проведем прямую `F L_1` , где `L_1` - середина ребра `ES`. Теперь проведем сечение `EBS`. Прямая `L L_1` будет средней линией треугольника, образованного осевым сечением пирамиды. `AL || FL_1`. Таким образом `FL_1` образована параллельным переносом `AL`. Рассмотрим плоскость `FBML_1`. Нам нужно найти угол между `FL_1` и `BM`. Параллельно перенесем прямую `BM`. Образуется треугольник `FB_1L_1`, в котором `FB_1 = sqrt(3)/4`, а `FL_1 = B_1L_1 = sqrt(1,5)`.
В чем моя ошибка?

@темы: Стереометрия, ЕГЭ

---

С ДНЕМ ПОБЕДЫ !

[~ghost]

С ПРАЗДНИКОМ ВСЕХ, КТО ПОСТОЯННО ПРИСУТСТВУЕТ НА ЭТОМ САЙТЕ, И ВСЕХ, КТО СЛУЧАЙНО СЮДА ЗАГЛЯНЕТ.
С ДНЕМ ПОБЕДЫ. С ДНЕМ ПАМЯТИ.

__________________________________________________________________________


В тот день, когда окончилась война
И все стволы палили в счет салюта,
В тот час на торжестве была одна
Особая для наших душ минута.

В конце пути, в далекой стороне,
Под гром пальбы прощались мы впервые
Со всеми, что погибли на войне,
Как с мертвыми прощаются живые.

До той поры в душевной глубине
Мы не прощались так бесповоротно.
Мы были с ними как бы наравне,
И разделял нас только лист учетный.

И только здесь, в особый этот миг,
Исполненный величья и печали,
Мы отделялись навсегда от них:
Нас эти залпы с ними разлучали.

Внушала нам стволов ревущих сталь,
Что нам уже не числиться в потерях.
И, кроясь дымкой, он уходит вдаль,
Заполненный товарищами берег

И, чуя там сквозь толщу дней и лет,
Как нас уносят этих залпов волны,
Они рукой махнуть не смеют вслед,
Не смеют слова вымолвить. Безмолвны.
…………………

Суда живых — не меньше павших суд.
И пусть в душе до дней моих скончанья
Живет, гремит торжественный салют
Победы и великого прощанья...

Александр Твардовский

@темы: Праздники

---

Помогите решить задание на ортогональное дополнение

[Alena94]

Вот задание: найти ортогональное дополнение к пространству M-подмножество R2[x]
M={f(x): ∫_0^1▒〖f(x)(x-9)dx=0}〗
(f,g)=∫_0^1▒f(x)g(x)dx

@темы: Линейная алгебра, Функциональный анализ

---

[ДОБРЫЙВЕЧЕР]

Дана правильная 6-угольная пирамида. M - середина ребра SC. Найти угол между BM и FS. (AS=...=FS=2, AB=...=FA=1)
BM=`sqrt(3/2)`

Помогите найти `alpha`

@темы: Стереометрия, ЕГЭ

---

проверьте двойной интеграл)

[ira_bodrova]

Вычислить интеграл: `iint_D x*sin(x+y)dxdy`, где область `D`: `{ 0 <= x <= pi ; 0 <= y <= pi/2 }`
Проверьте, пожалуйста:

@темы: Кратные и криволинейные интегралы, Интегралы

---

C5

[Arcan]

При каких значениях параметра `p` уравнение не имеет корней
`4sin^3(x)+3cos(2x)+p=0`

@темы: Тригонометрия, Задачи с параметром, ЕГЭ

---

Гиа.

[Команданте Че]

Добрый вечер.
Буду очень благодарна тем, кто поможет. У меня нет совершенно никаких идей, ну вот вообще. То ли я уже перерешалась задач, то ли уже совсем ку-ку.
Хотя они, по идее, легкие должны быть.

1. Известно, что в равнобедренную трапецию, периметр которой равен 80, а острый угол при основании равен 30, можно вписать окружность. Найдите площадь трапеции.
2. Найдите площадь правильного 8-угольника, если длина его меньшей диагонали равна 3*root(4)(2).
3. А вот в этом условии, мне кажется, опечатка.
Площадь треугольника ABC равна 12. Из вершины тупого угла B проведена медиана BD, длина которой равна 12, и которая перпендикулярна стороне AB. Найдите длину стороны AC.

@темы: Планиметрия, ГИА (9 класс)

---

Задачка на доказательство (Обратный оператор)

[Nevemore]

Мне нужно доказать что линейный оператор имеет обратный оператор тогда и только тогда когда 0 не является собственным значением этого оператора.
Решение: Пойдем от противного, пусть 0 является собственным числом, тогда `Ax=s*x` => матрица A - состоит из 0 = > A - вырожденная => не имеет обратную ( из теоремы о том, что матрица имеет обратную тогда и только тогда, когда она не вырожденная. ) Тут возник вопрос а может ли быть матрица А вырожденной вообще?

@темы: Линейная алгебра

---

Помогите,пожалуйста

[Hoshie]

1. 1. Найти область определения функции двух переменных. Изобразить ее на координатной плоскости и заштриховать.
2. Проверить, удовлетворяет ли функция двух переменных указанному дифференциальному уравнению.
1. `z=ln(x*(y-1))`
2. `z=(ln(x-y))/x, \ \ d/(dx) [x^2*(dz)/(dx)] = x^2*(d^2 z)/(dy^2)`

2. Найти наименьшее и наибольшее значения функции в замкнутой области
D, заданной системой неравенств. Сделать чертеж.
`z=x^3+y^3-9*x*y-25; \ \ 0 <=x <= 5; \ \ 0 <=y <= 5.`

@темы: Функции нескольких переменных

---

Найдите наибольшее значение функции

[feride_24_07_96]

Найдите наибольшее значение функции
`y=-x^2+px+q`, если её график проходит через точки P(-1;-13) и Q(3;-1)

@темы: Школьный курс алгебры и матанализа, Исследование функций

---

Вычислить предел последовательности

[alligator76]

Необходимо вычислить предел последовательности или доказать расходимость:

2,1; 2,11; 2,111; ...

С общим членом ряда у меня получилось следующее:

`a_n=2+sum_(k=1)^n (1/10)^k`

И как найти предел этой последовательности?

@темы: Пределы, Прогрессии

---

Сборник задач по теории вероятностей, математической статистике и теории случайных ве

[pemac]

Свешников А.А. Сборник задач по теории вероятностей, математической статистике и теории случайных величин - Изд.: Лань, 2008, 448 стр. Сборник охватывает все основные разделы теории вероятностей, встречающиеся при решении практических вопросов, связанных с автоматизированным управлением, обработкой опытных данных, установлением их точности и т.д. Задачи снабжены ответами, а в отдельных случаях указаниями к решению. В конце задачника приложены краткие таблицы для вероятностных расчетов, необходимые при решении ряда задач. Учебное пособие предназначено для студентов, специализирующихся в области прикладной математики, а также экономики, финансов, информационной безопасности, математической экономики, кибернетики и т.д. Скачать (djvu) ifolder.ru Версия от alprobyte с ocr www.mediafire.com || || www.mediafire.com

@темы: Задачник, Теория вероятностей

---

[ДОБРЫЙВЕЧЕР]

Дана правильная 6-угольная пирамида, стороны основания = 1, боковые ребра = 2. M - середина ребра SC. Найти синус угла между BM и DE.

На рисунке я изобразил угол, который надо найти, сторона BM=`sqrt(1,5)`. Помогите с поиском третьей стороны

@темы: Стереометрия, ЕГЭ

---

Помогите пожалуйста с задачей!

[kssu1994]

Основанием пирамиды служит треугольник со сторонами а, а и в. Все боковые рёбра наклонены к плоскости основания под углом 60 градусов. Определить объём пирамиды.

@темы: Стереометрия

---

Ряды

[ritmix10]

Всем всем привет=)
Помогите пожалуйста с разложением:
Нужно разложить функцию f(t) в ряд Фурье, считая, что одну половину периода `f=a<0` а другую половину периода `f(t)=a+Vcoswt`. Нарисовать спектрограмму.
начал делать вот так
`a0 = 1/2[int_0^(pi) a*dt + int_(pi)^(2pi) (a+Vcoswt)dt = pi*a+V/(2w) * sin(w*pi)`
`a1 = 1/2[int_0^(pi) a*cos[wt]dt + int_(pi)^(2pi) (a+Vcoswt)*cos[wt]dt = a/(2w)*sin[2*pi*w]+(pi*V)/4-1/4*sin[2*pi*w]+1/4*sin[4*pi*w]`

так??? а дальше вроде зацикливание получается...

@темы: Ряды

---

Ищу учебник

[Бифи]

Ищу учебник Геометрия 7,8,9 Александров, Вернер

@темы: Поиск книг, Планиметрия

---

Где найти?

[TAJlOS]

При решении некоторых задач по ТЧ, наткнулся на некоторые свойства. Например свойство: квадрат натурального числа не может давать при делении на 3 остаток 2. Читал некоторые книги по ТЧ и разделы в школьной углублённой литературе, но описание подобных свойств не нашёл.
Хотелось бы узнать где можно прочесть про подобные свойства.

@темы: Поиск книг, Олимпиадные задачи, Теория чисел

---

Помощь с контрольной работой(10 класс.Вероятность)

[JuliaCrowd]

Здравствуйте!
Я услышала об этом сообществе от подруги, не могли бы вы подсказать, как решать эти два номера:
1. Сколько четырехзначных чисел можно составить из цифр 1,2,3,4 , при условии что каждая цифра может содержаться в записи числа нечетное количество раз?
(Пробовала решать при помощи правила умножения, но не понятно какой правильный ход:
1ую цифру можно выбрать 4мя способами, 2ую тоже 4мя, 3ю также 4мя, а последнюю 3мя
не знаю правильно ли рассуждаю)

2.В разложении бинома `(sqrt(x^3)+1/(x^4))^n` коэффициент 3 члена на 44 больше коэффициента второго члена. Найти член независящий от x.
(Сначала нужно найти n, из (С из х по 3 минус С из х по 2 равно 44) однако почему то при разложении С получается ужасное кубическое уравнение.)


Заранее спасибо за уделенное время!

@темы: Комбинаторика

---

[ДОБРЫЙВЕЧЕР]

Дано:
`ABCDEFS` - правильная 6-угольная пирамида;
`G` лежит на ребре SC;
`(SG)/(GC)=1/2`
`BC` = 4;
`AS=...=FS=3*(sqrt(6))`
------------------------------
Найти угол между `AD` и `BG`

Так как `AD` параллельна `BC`, то искомый угол `GBC`. В этом треугольнике известны стороны `BC` и `GC`. Подскажите, как найти `BG`?

@темы: Стереометрия, ЕГЭ

---

площадь плоской фигуры

[Snka]

Помогите, пожалуйста решить:
Вычислить площадь плоской фигуры, ограниченной линиями: `3x^2-2y=0` `2x+2y-1=0`
1. Объединила правые части уравнений :`3x^2+2x-1=0` отсюда, `x_1=1/3`; `x_2=-1`` y_1=0.17` `y_2=1.5`;
координаты точек (А(0.33;0.17); B(-1;1/5) (график не чертила, не знаю нужно ли)
2. Площадь находила по формуле: `S=\int_{x_1}^{x_2}f(x)-g(x)dx` (не уверена, что по этой формуле нужно вычислять)
`S=\int_{0.33}^{-1}((3x^(2)/2)-((2x-1)/2)dx`=`-\int_{-1}^{0.33}(x^2-x)dx`=`-((x^(3)/3)-x)|_{-1}^{0.33}`=`-1.012`
ответ почему-то отрицательный получился, площадь ведь не может быть отрицательной. Ошибку найти не могу.

@темы: Приложения определенного интеграла, Интегралы