MZ3
`TZ`Используя интеграл Пуассона, вычислить интеграл
`int_0^(+oo)(x*e^(-ax^2)*sinbxdx`[[/TZ]]
читать дальше
Я решала его по частям, но ничего не получилось(((
`TZ`Используя интеграл Пуассона, вычислить интеграл
`int_0^(+oo)(x*e^(-ax^2)*sinbxdx`[[/TZ]]
читать дальше
Я решала его по частям, но ничего не получилось(((
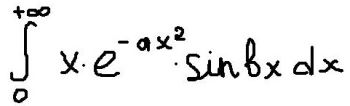
-
-
09.03.2009 в 02:43вроде по частям и надо.. видно плохо(
-
-
09.03.2009 в 02:50-
-
09.03.2009 в 02:53-
-
09.03.2009 в 02:54-
-
09.03.2009 в 03:15Это соответствует вашему уровню сложности задач?
-
-
09.03.2009 в 03:18erf в Maple - это Q-функция или интеграл вероятности?
судя по ответу, здесь не по частям...
-
-
09.03.2009 в 03:20Правильная картинка вот:
-
-
09.03.2009 в 03:35-
-
09.03.2009 в 03:36-
-
09.03.2009 в 03:36Да я вот сам думаю...
Вам к какому сроку нужно?
-
-
09.03.2009 в 03:39-
-
09.03.2009 в 03:51Косинус представляется в сумму экспонент, и таким образом получаются два интеграла ошибок, которые при подсчете упрощаются до моего ответа.
---------------------
Итак:
1) Исходный - по частям - избавляемся от "x"
2) ∫ exp(-ax^2)*cos(bx) dx - используя тот факт, что косинус = сумма двух экспонент. Комплексные значения erf в конечном итоге сократятся.
P.S.
erf(0) = 0
erf(infinity) = 1
На вопросы, видимо, если они будут, отвечу после сна.
-
-
09.03.2009 в 04:12-
-
09.03.2009 в 10:13cos расписываешь в сумму двух экспонент по формуле, что я дал
Получаются два интеграла вида exp(-ax^2)*exp(-bix) - значения коэффициентов там другие какие-то
-
-
09.03.2009 в 12:29-
-
09.03.2009 в 12:31-
-
09.03.2009 в 14:33Способ нахождения интеграла, пользуясь только интергалом Пуассона мне неизвестен.
Я его решил, но у меня получился сдвиг в переменной.
Ну, пример, ∫ exp(-(x-1)^2) dx
Это в свою очередь сдвигает пределы интегрирования - и получается уже не интеграл Пуассона, а более общий вид - интеграл ошибок (erf).
Если действовать строго, то нужно действовать, примерно, как тут:
www.nsu.ru/matlab/Exponenta_RU/educat/class/cou...
К сожалению, объяснить полностью строгие выкладки я не могу - комплексный анализ я знаю плохо.
Но можно немного схитрить и обойти комплексный анализ стороной, используя запись erf(x+p), где p - комплексное число. Комплексные значения просто сократятся..
-
-
09.03.2009 в 14:572}}} \left( {e^{{\it ix}}}+{e^{-{\it ix}}} \right) {dx} = 1/2\,\int \!{e^{-{x}^{2}+{\it ix}}}{dx}+1/2\,\int \!{e^{-{x}^{2}-{\it
ix}}}{dx}=1/2\,{e^{-1/4}}\int \!{e^{- \left( x-1/2\,i \right) ^{2}}}{d
x}+1/2\,{e^{-1/4}}\int \!{e^{- \left( x+1/2\,i \right) ^{2}}}{dx}
Переводите это в
1/4\,{e^{-1/4}}\sqrt {\pi }{\it erf} \left( x+1/2\,i \right)
и
1/4\,{e^{-1/4}}\sqrt {\pi }{\it erf} \left( x-1/2\,i \right)
И осталось решить, как несобственные интегралы по двум пределам.
На коды не обращай внимания. Картинки видны?
-
-
09.03.2009 в 15:40-
-
17.12.2009 в 15:33Решаю интеграл:
В процессе следую Вашей схеме, получаю следующее:
На сайте www.sosmath.com/tables/integral/integ38/integ38... имеется решение этого интеграла, но только с другими пределами. Решения Maple красивого результата не дают.
Спасибо заранее
-
-
17.12.2009 в 15:44Дык вроде тоже самое... Свести к erf() и вычислить несобственные интегралы.
-
-
17.12.2009 в 17:16Спасибо за ответ
Просто в моём случае всё время получается, что при сворачивании в квадрат суммы или разности, комплексное i выносится в множителе exp((i-alpha)^2/2*mu) и нигде не сокращается.
-
-
17.12.2009 в 20:02Ты, наверное не понял мысль.
Сразу сокращаться не должно.
www.diary.ru/~eek/p63657366.htm?from=last&discu...
Получаются две erf с комплексами, подставляешь туда пределы интегрирования и только после этого исходя из свойств erf можно будет что-то сократить.
-
-
18.12.2009 в 13:16первый интеграл:
Второй интеграл:
Экспонента с параметром и с i выносится и в любом случае комплексность остаётся.
Может быть, я не понял, как свести к erf и этой комплексности не будет?
Я уже, можно сказать, в отчаянии )
-
-
18.12.2009 в 13:24-
-
18.12.2009 в 13:32Покопаюсь, примерно через час напишу про итоги.
-
-
18.12.2009 в 13:40-
-
18.12.2009 в 14:511) В maple ответ громоздкий потому, что в зависимости от мю функция может быть сходящаяся или расходящаяся. Поэтому в нем необходимо дописать строчку assume(мю>0).
2) Даже с учетом этой приписки ответ там выражается через комплексы, но это не страшно, я думаю, по-другому не записать без геморроя.
3) Ответ в справочниках дан в комплексах (стр. 367 Прудников, Брычков, Маричев.) или Градштейн (стр. 494)
4) В maple появляется cos() - видимо, выдирается по этой формуле.
P.S. Как вариант, без комплексов, можно разложить в ряд (либо сразу, либо разложить в ряд выражение exp()*erf() + exp()*erf() и сократить комплексы - проще сразу разложить и интегрировать ряд), получить некоторый ряд и попробовать свернуть в maple (для начала с какими-то простенькими параметрами типа a=1/2, b=1, потом, если получится, в общем виде)
-
-
18.12.2009 в 14:55-
-
18.12.2009 в 15:08