Примечание Robot:Большая просьба к решателям - посмотрите. пожалуйста, эти задачи. Срок истекает. Я тоже с формулой Тейлора не в ладах, а кроме того, я весь день решала и уже плохо соображаю. Пожалуйста!!!!
Добрый вечер,
Не знаю , как решать 4 примера из зачетной работы 1 курс, в особенности примеры на формулу Тейлора.
Возможно кто-нибудь сможет подсказать с чего начать?..
4г)Сделано, спасибо за помощь)
Найти предел, используя разложение по формуле Тейлора:
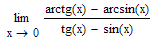
С формулой Тейлора у меня мягко говоря плохо... В этом примере синус я допустим раскладываю до какого-то порядка(кстати до какого?), а что делать с арктангенсом , арксинусом и тангенсом? На Тейлора решали буквально пару примеров, поэтому в этой теме не силен..
5)Сделано, спасибо за помощь)
Используя определение(б.м. х соотв. б.м.
х соотв. б.м.  у) доказать непрерывность в области определения :
у) доказать непрерывность в области определения :

Я не знаю определения непрерывности через дельты , в этом наверное и проблема. Не могли бы подсказать определение непрерывности через дельты?
6б)Сделано, спасибо за помощь)
На множесте х=(- ;
; ) найти точки разрыва, определить их характер, изобразить графически:
) найти точки разрыва, определить их характер, изобразить графически:
у(х) =
Слабо себе представляю , как выглядит данный график... первые раз вижу график с пределом... А подозрительные на разрыв точки(а) расположены в знаменателе, я прав?
12) Разложить по формуле Тейлора в окрестности точки до
до  :
:
у(х) =
Опять же у меня очень плохи дела с формулой Тейлора ... может есть некоторые онлайн - примеры подобные этому примеру?
Буду признателен за помощь!
Сроки - сегодяшний вечер(23:00-24:00 по Москве).
Добрый вечер,
Не знаю , как решать 4 примера из зачетной работы 1 курс, в особенности примеры на формулу Тейлора.
Возможно кто-нибудь сможет подсказать с чего начать?..
4г)Сделано, спасибо за помощь)
Найти предел, используя разложение по формуле Тейлора:
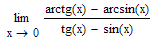
С формулой Тейлора у меня мягко говоря плохо... В этом примере синус я допустим раскладываю до какого-то порядка(кстати до какого?), а что делать с арктангенсом , арксинусом и тангенсом? На Тейлора решали буквально пару примеров, поэтому в этой теме не силен..
5)Сделано, спасибо за помощь)
Используя определение(б.м.
 х соотв. б.м.
х соотв. б.м.  у) доказать непрерывность в области определения :
у) доказать непрерывность в области определения :
Я не знаю определения непрерывности через дельты , в этом наверное и проблема. Не могли бы подсказать определение непрерывности через дельты?
6б)Сделано, спасибо за помощь)
На множесте х=(-
 ;
; ) найти точки разрыва, определить их характер, изобразить графически:
) найти точки разрыва, определить их характер, изобразить графически:у(х) =

Слабо себе представляю , как выглядит данный график... первые раз вижу график с пределом... А подозрительные на разрыв точки(а) расположены в знаменателе, я прав?
12) Разложить по формуле Тейлора в окрестности точки
 до
до  :
:у(х) =

Опять же у меня очень плохи дела с формулой Тейлора ... может есть некоторые онлайн - примеры подобные этому примеру?
Буду признателен за помощь!
Сроки - сегодяшний вечер(23:00-24:00 по Москве).
-
-
22.12.2007 в 02:03в 6б
Если x<0 то предел + Infinity для экспоненты превращается в -Infinity (!!!) -> e^(nx) = e^(-Infinity) = 0
И функция вырождается в параболу! (2x^2+0)/(1+0)=2x^2.
Так что график не врет.
-
-
22.12.2007 в 14:03Там вообще так славно выходит....
Блин, значит надо вообще рассматривать два предела отдельно: при х>0 и х<0...
А как так получается, что х на графике положительных значений вообще не принимает?
-
-
22.12.2007 в 14:27А зачем его строить при n=1???
Вообщем это разрыв второго рода:
0- = 0
0 = 1
0+ = +infinity
-
-
22.12.2007 в 14:55У меня в maple - отобразилось. Там гипербола, причем тем больше n, тем график больше похож на гиперболу.
-
-
22.12.2007 в 14:56Если постепенно увеличивать n, понятно, что там в итоге происходит:
-
-
22.12.2007 в 14:57-
-
22.12.2007 в 14:57-
-
22.12.2007 в 15:02А то меня всё снедали сомнения, куда он в положительной полуоси девается...
-
-
23.12.2007 в 03:13там же всё просто.
sinx = x - x^3/3! + x^5/5! .. + (-1)^(m-1)*x^(2*m-1)/(2*m-1)! + o(|x^(2m-1)|)
cosx = 1 - x^2/2! + x^4/4! + .. + (-1)^m * x^(2m)/(2m)! + o(x^2m)
Соотвественно в этом примере выписываешь Pi/4 * (cosx + sinx) + x(cosx +sinx)
Ну и умножаешь.
По идее всё.
-
-
11.01.2011 в 00:33