| |
Even as the finite encloses an infinite series
And in the unlimited limits appear,
So the soul of immensity dwells in minutia
And in the narrowest limits no limit in here.
What joy to discern the minute in infinity!
The vast to perceive in the small, what divinity!
Как в конечном содержатся бесконечные ряды,
Как безграничное вдруг оказывается ограниченным,
Так дух необъятности обитает в мелочах
И в теснейших границах таится беспредельность.
Какая радость суметь различить мельчайшее в бесконечности!
Как божественно увидеть бескрайность в малом!
Якоб Бернулли. «Искусство предположений»
|
Сегодня,
27 декабря, день рождения одного из самых известных и плодовитых математиков не только семьи Бернулли, но всех времен и народов. Сегодня исполняется
360 лет со дня рождения
Якоба Бернулли.

Википедия
Якоб Бернулли (нем. Jakob Bernoulli, 27 декабря 1654, Базель, — 16 августа 1705, там же) — швейцарский математик, профессор математики Базельского университета (с 1687 года). Один из основателей теории вероятностей и математического анализа. Старший брат Иоганна Бернулли. Иностранный член Парижской Академии наук (1699) и Берлинской академии наук (1701).
БиографияЯкоб родился в семье преуспевающего фармацевта Николая Бернулли. Вначале, по желанию отца, учился в Базельском университете богословию, но увлёкся математикой, которую изучил самостоятельно. В университете овладел также 5 языками (французский, итальянский, английский, латинский, греческий), в 1671 году получил учёную степень магистра философии.
В 1676-1680 годах совершил поездку по Европе. Заехал во Францию для изучения идей Декарта, затем в Италию. Вернувшись в Базель, некоторое время работал частным учителем.
В 1682 году отправился в новое путешествие, навестив Нидерланды и Англию, где познакомился с Гюйгенсом, Гуком и Бойлем. В 1684 году, по возвращении в Базель, женился на Юдит Штупанус (Judith Stupanus), у них родились сын и дочь.
В 1683 году начал читать лекции по физике в Базельском университете. С 1687 года избран профессором физики (с 1687 года — математики) в этом университете.
1687: обнаружил первый мемуар Лейбница (1684 года) по анализу и с энтузиазмом начал освоение нового исчисления. Обратился с письмом к Лейбницу с просьбой разъяснить несколько тёмных мест. Ответ он получил только спустя три года (1690, Лейбниц тогда был в командировке в Париже); за это время Якоб Бернулли самостоятельно освоил дифференциальное и интегральное исчисление, а заодно приобщил к нему брата Иоганна. По возвращении Лейбниц вступил в активную и взаимно-полезную переписку с обоими. Сложившийся триумвират — Лейбниц и братья Бернулли — 20 лет возглавлял европейских математиков и чрезвычайно обогатил новый анализ.


Эпитафия и спираль на гробнице Якоба Бернулли
В 1692 году у Якоба Бернулли обнаружились первые признаки туберкулёза, от которого он и скончался в 1705 году. В честь Якоба и Иоганна Бернулли назван кратер на Луне.
Научная деятельностьчитать дальшеПервое триумфальное выступление молодого математика относится к 1690 году. Якоб решает задачу Лейбница о форме кривой, по которой тяжелая точка опускается за равные промежутки времени на равные вертикальные отрезки. Лейбниц и Гюйгенс уже установили, что это полукубическая парабола, но лишь Якоб Бернулли опубликовал доказательство средствами нового анализа, выведя и проинтегрировав дифференциальное уравнение. При этом впервые появился в печати термин «интеграл».
Якоб Бернулли внёс огромный вклад в развитие аналитической геометрии и зарождение вариационного исчисления. Его именем названа лемниската Бернулли. Он исследовал также циклоиду, цепную линию, и особенно логарифмическую спираль. Последнюю из перечисленных кривых Якоб завещал нарисовать на своей могиле; по невежеству там изобразили спираль Архимеда, см. фотографию справа. Согласно завещанию, вокруг спирали выгравирована надпись на латыни, «EADEM MUTATA RESURGO» («изменённая, я вновь воскресаю»), которая отражает свойство логарифмической спирали восстанавливать свою форму после различных преобразований.
Якобу Бернулли принадлежат значительные достижения в теории рядов, дифференциальном исчислении, теории вероятностей и теории чисел, где его именем названы «числа Бернулли».


«Искусство предположений»
Он изучил теорию вероятностей по книге Гюйгенса «О расчётах в азартной игре», в которой ещё не было определения и понятия вероятности (её заменяет количество благоприятных случаев). Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей и сформулировал первый вариант закона больших чисел. Якоб Бернулли подготовил монографию в этой области, однако издать её не успел. Она была напечатана посмертно, в 1713 году, его братом Николаем, под названием «Искусство предположений» (Ars conjectandi). Это содержательный трактат по теории вероятностей, статистике и их практическому применению, итог комбинаторики и теории вероятностей XVII века. Имя Якоба носит важное в теории вероятностей распределение Бернулли.
Якоб Бернулли издал также работы по различным вопросам арифметики, алгебры, геометрии и физики.
Распределение Бернулличитать дальшеДумаю, нет ни одного студента, прослушавшего курс теории вероятностей, который не знал бы, что такое распределение Бернулли.
Распределение Бернулли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи.
Случайная величина X имеет распределение Бернулли, если она принимает всего два значения: 1 и 0 с вероятностями p и q = 1-p соответственно. Таким образом:
P(X=1) = p,
P(X=0) = q.
Принято говорить, что событие X=1 соответствует «успеху», а X=0 «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
Моменты распределения Бернулли
E[X] = p,
D[X] = pq.
Вообще, легко видеть, что
E[X^n] = p, для любой натуральной степени n.Числа Бернулличитать дальшеЧисла Бернулли — последовательность рациональных чисел `B_0, B_1, B_2, ...`, впервые рассмотренная Якобом Бернулли в связи с вычислением суммы последовательных натуральных чисел, возведённых в одну и ту же степень:

где  — биномиальный коэффициент.
— биномиальный коэффициент.
Свойства
- Все числа Бернулли с нечётными номерами, кроме `B_1`, равны нулю, а знаки чисел Бернулли с чётными номерами чередуются.
- Числа Бернулли являются значениями многочленов Бернулли `B_n(x)` при `x=0`: `B_n = B_n(0)`.
Числа Бернулли часто входят в коэффициенты разложения элементарных функций в степенной ряд.


Написана в 1713 г.


Лемнискаты с тремя фиксированными фокусами
Примеры
- Лемнискатой с одним фокусом (n=1) является окружность радиуса r, а с двумя фокусами — овал Кассини.
- Частным случаем овала Кассини является лемниската Бернулли, по имени швейцарского математика Якоба Бернулли, положившего начало изучению лемнискат.
Лемниската Бернулли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.
Лемниската по форме напоминает восьмёрку или символ бесконечности. Точка, в которой лемниската пересекает саму себя, называется узловой или двойной точкой.


Лемниската и её фокусы
Название происходит от др.-греч. λημνίσκος — лента, повязка. В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Данный вид лемнискаты назван в честь швейцарского математика Якоба Бернулли, положившего начало её изучению.
Уравнение лемнискаты впервые опубликовано в статье Curvatura Laminae Elasticae Якоба Бернулли в журнале Acta eruditorum в 1694 году. Бернулли назвал эту кривую lemniscus; он не знал, что четырнадцатью годами ранее Джованни Кассини уже исследовал более общий случай. Квадратуру лемнискаты впервые выполнил Джюлио-Карло Фаньяно (англ.), опубликовав в 1718 году статью Metodo per misurare la lemniscata и положив тем самым начало изучению эллиптических интегралов, продолженное впоследствии Леонардом Эйлером. Некоторые свойства кривой были также исследованы Якобом Штейнером в 1835 году.
Уравнения
Рассмотрим простейший случай: если расстояние между фокусами равняется 2c, расположены они на оси OX, и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:
- в прямоугольных координатах:

- в полярных координатах:

- Параметрическое уравнение в прямоугольной системе:

где 
Это единственный вариант рациональной параметризации кривой. Уравнение полностью описывает кривую, когда параметр пробегает всю вещественную прямую: от -oo до +oo. При этом, когда параметр стремится к -oo, точка кривой стремится к (0;0) из второй координатной четверти, а когда параметр стремится к +oo, то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.


Плотность точек кривой при равномерном изменении параметра
Гравитационное свойство лемнискаты


Материальная точка, движущаяся по лемнискате под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду (см. рисунок). Предполагается, что ось лемнискаты составляет угол 45o с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.
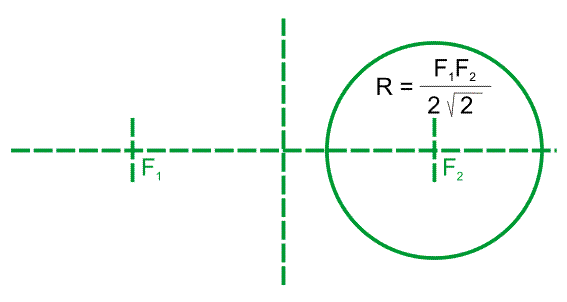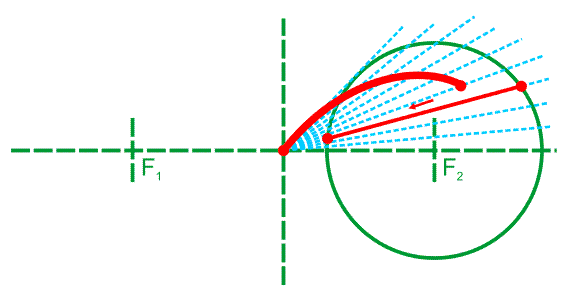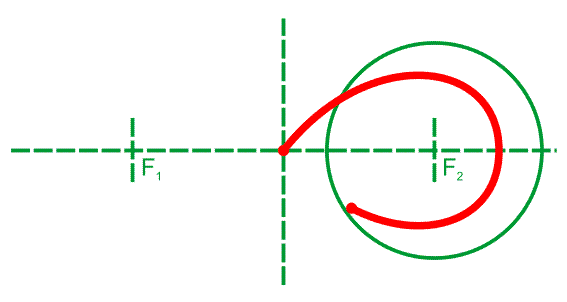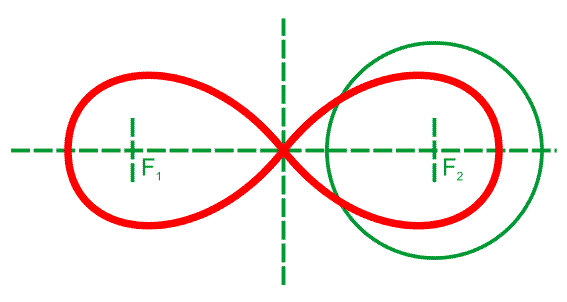

Построение лемнискаты при помощи секущих
Шарнирные методы построения
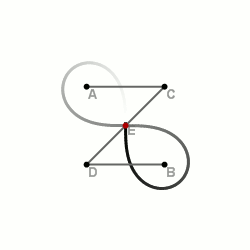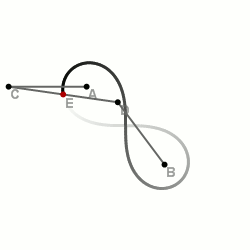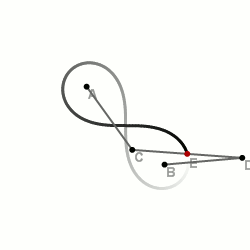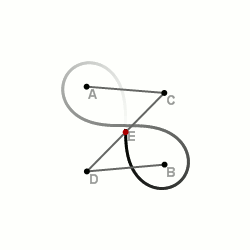

Шарнирный метод


Механизм Ватта
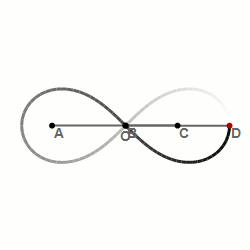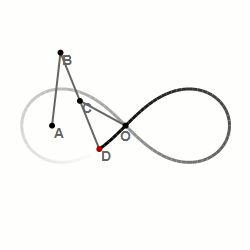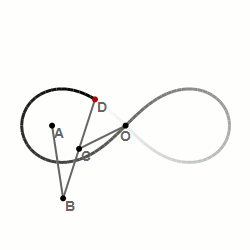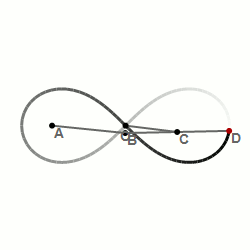
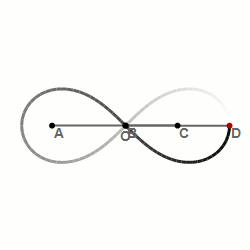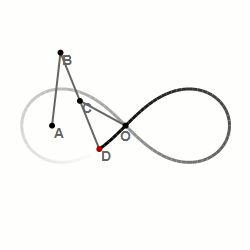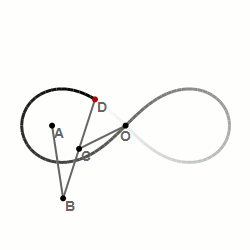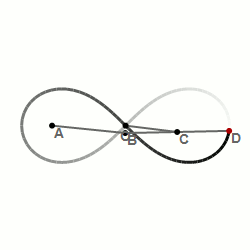
Другой вариант шарнирного метода
Ссылки






 — биномиальный коэффициент.
— биномиальный коэффициент.











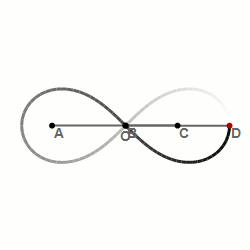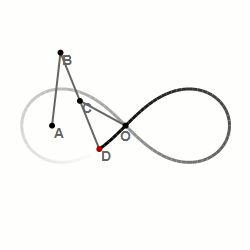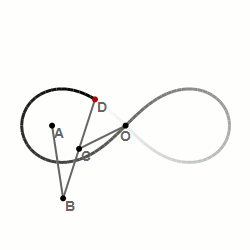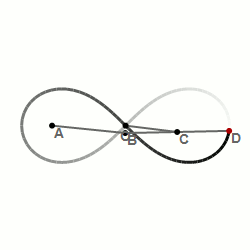
-
-
27.12.2014 в 21:37..
-
-
27.12.2014 в 21:59Спасибо!
Исправила.
У меня столько интеллектуальных усилий ушло на перевод стиха, что всё остальное я уже практически на остатках силы воли делала )))
Заметила эту комбинаторику. Удивилась. Но исправить даже в голову не пришло ))
У чисел Бернулли в правой части `N` - это что?...
Я так понимаю, что `N` это количество слагаемых в левой части.
Но это как-то странно..Сейчас посмотрю где-нибудь еще...
-
-
27.12.2014 в 22:10-
-
27.12.2014 в 22:14Нашла ссылку на Квант на сайте МЦНМО, но она сейчас недоступна...
Надеюсь, потом всё наладится. Хочу почитать
kvant.mccme.ru/1974/06/chisla_bernulli.htm
-
-
27.12.2014 в 22:26В первый раз пропустил закладку с лемнискатой ... а там столько красивого!!...
-
-
27.12.2014 в 22:49Ага. Хотя тоже копипаст всё... Так что, моя заслуга невелика...
Когда писала про лемнискату (про гравитационное свойство), было жуткое ощущение дежа вю... Казалось, что уже писала про нее... Все сообщество перевернула — не нашла...
А потом вспомнила! Оказалось, что это было про брахистохрону... ))
eek.diary.ru/p193232421.htm