Друзья, это было так давно, что все уже забыл... Есть ли аналитическое решение для такого дифура:
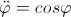
`ddot phi=cos phi`
Вторая производная по времени равна косинусу функции (если плохо видно).
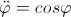
`ddot phi=cos phi`
Вторая производная по времени равна косинусу функции (если плохо видно).
-
-
19.03.2012 в 13:38-
-
19.03.2012 в 14:05-
-
19.03.2012 в 14:24-
-
19.03.2012 в 14:52-
-
19.03.2012 в 15:07-
-
19.03.2012 в 15:11-
-
20.03.2012 в 09:16-
-
20.03.2012 в 15:14