воскресенье, 08 февраля 2015
Помогите пожалуйста найти угол А в треугольнике с вершинами А(1;2√3), В(-1;0), С(1;0)
суббота, 07 февраля 2015
Найти уравнение перпендикуляра, проходящего через точку А(-3,-2,1) к прямой x+2\2=y-2\3=z-3\1. По какой формуле?
Биссектрисы треугольника `ABC` `A A_1`, `B B_1` и `C C_1` пересекаются в точке `O`. Известно, что `(AO) / (OA_1)=5/1`, `(CO) / (OC_1)=5/4`. Точка `H` – пересечение отрезков `A_1 C_1` и `B B_1`. Найти `(C_1H) / (HA_1)`
(ответ: 3/2).
читать дальше
Не могу понять, с чего начать решать. По свойству биссектрисы треугольника,
`(BA_1)/(CA_1)=(AB)/(AC)`.
Аналогично для остальных двух биссектрис.
Но в задаче даны именно "внутренние отношения", т.е., как мне кажется, нужно работать с треугольниками `AOC` и `A_1 O C_1`. Мне кажется, что эти треугольники подобны, но доказать это я не могу.
Прошу помощи.
(ответ: 3/2).
читать дальше
Не могу понять, с чего начать решать. По свойству биссектрисы треугольника,
`(BA_1)/(CA_1)=(AB)/(AC)`.
Аналогично для остальных двух биссектрис.
Но в задаче даны именно "внутренние отношения", т.е., как мне кажется, нужно работать с треугольниками `AOC` и `A_1 O C_1`. Мне кажется, что эти треугольники подобны, но доказать это я не могу.
Прошу помощи.
Здравствуйте! Нужна информация о том, как связаны между собой геометрические преобразования плоскости (параллельный перенос на вектор, поворот вокруг точки на данный угол, гомотетия) с комплексной плоскостью. Мне объясняли так: если есть точка `z` на комплексной плоскости, то, например, перенос на вектор этой точки можно записать в виде функции как `f(z)=z+c`. То есть если точка `z=0+0i`, то отображение `f(z)=z+(5+4i)` переводит эту точку параллельным переносом в точку `z1=5+4i`. Если нужно повернуть на угол, то добавляется мнимая единица `i` (так мне сказали, но не понимаю почему). Где об этом можно подробно прочитать? И связано ли это как-то с уравнениями параллельного переноса, поворота, гомотетии на плоскости?
пятница, 06 февраля 2015
Добрый вечер!
Такое задание:
Доказать, что `A=(sum_(i = 1)^(n)((x_i - bar(x))*y_i))/(sum_(i = 1)^n(x_i - bar(x))^2)` имеет асимптотически нормальное распределение.
Причем
`E(y_i) = 0` (1)
`var(y_i) = sigma^2` (2)
`E(y_i,y_j) = 0` при `i != j` (3)
Распределение `y_i` не зависит от `x_1^(j), ldots, x_n^(j)` для всех `j = 1, ldots, k` (4)
Также про `x` известно, что их значения извлечены случайным образом из некоторой генеральной совокупности и что они линейно независимы.
Думаю свести данное выражение к центральной предельной теореме. Но возникает вопросы:
Следует ли из условий (1) и (2), что случайные величины `y_i` одинаково распределены?
Следует ли из того, что `x_i` извлечены из одной генеральной совокупности, что они одинаково распределены?
Нужно ли преобразовывать выражение?
Заранее спасибо за помощь)
Такое задание:
Доказать, что `A=(sum_(i = 1)^(n)((x_i - bar(x))*y_i))/(sum_(i = 1)^n(x_i - bar(x))^2)` имеет асимптотически нормальное распределение.
Причем
`E(y_i) = 0` (1)
`var(y_i) = sigma^2` (2)
`E(y_i,y_j) = 0` при `i != j` (3)
Распределение `y_i` не зависит от `x_1^(j), ldots, x_n^(j)` для всех `j = 1, ldots, k` (4)
Также про `x` известно, что их значения извлечены случайным образом из некоторой генеральной совокупности и что они линейно независимы.
Думаю свести данное выражение к центральной предельной теореме. Но возникает вопросы:
Следует ли из условий (1) и (2), что случайные величины `y_i` одинаково распределены?
Следует ли из того, что `x_i` извлечены из одной генеральной совокупности, что они одинаково распределены?
Нужно ли преобразовывать выражение?
Заранее спасибо за помощь)
ключник
Помогите, пожалуйста, преобразовать к итерационному виду.
функция `y=e^(2x)+3x-4`
Промежуток поиска корня выбран с помощью графика.

Беда в том, что производная от этой итерационной функции не соответствует условию, согласно которому она должна быть от -1 до 0 чтобы получился двусторонний сходящийся процесс), хотя из этих самых условий и искалась. С помощью вот этой методички делалось, но там не всё ясно.
Если просто подставлять выбранное тау в (20), выходит 1/2 при любых х. Что я делаю неправильно?
функция `y=e^(2x)+3x-4`
Промежуток поиска корня выбран с помощью графика.

Беда в том, что производная от этой итерационной функции не соответствует условию, согласно которому она должна быть от -1 до 0 чтобы получился двусторонний сходящийся процесс), хотя из этих самых условий и искалась. С помощью вот этой методички делалось, но там не всё ясно.
Если просто подставлять выбранное тау в (20), выходит 1/2 при любых х. Что я делаю неправильно?
четверг, 05 февраля 2015
 |
Чулков П. Тринадцать турниров Архимеда / П. Чулков. – М. : Чистые пруды, 2005. – 32 с. (Библиотечка «Первого сентября», серия «Математика».) |
среда, 04 февраля 2015
14:42
Доступ к записи ограничен
Step by step ...
Закрытая запись, не предназначенная для публичного просмотра
вторник, 03 февраля 2015
Тигр, Тигр, жгучий страх, Ты горишь в ночных лесах. Чей бессмертный взор, любя, Создал страшного тебя?
Объясните пожалуйста человеческим языком этот критерий... Что такое множество лебеговой меры нуль ? Измеримое по Жордану множество ?
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Задача: Две вершины жёсткого треугольника двигаются по паре фиксированных пересекающихся прямых. Докажите, что третья вершина треугольника двигается по некоторому эллипсу или отрезку прямой.
Моё решение: (проверьте, пожалуйста, на наличие ошибок)
1 часть: cloud.mail.ru/public/babc0ca32552/IMG_20150203_...
2 часть: cloud.mail.ru/public/687275c61715/IMG_20150203_...
P.S: простите за плохое качество фотографий, был только телефон.
Моё решение: (проверьте, пожалуйста, на наличие ошибок)
1 часть: cloud.mail.ru/public/babc0ca32552/IMG_20150203_...
2 часть: cloud.mail.ru/public/687275c61715/IMG_20150203_...
P.S: простите за плохое качество фотографий, был только телефон.
Пользуясь алгоритмом Евклида, подобрать многочлены М1(х) и М2(х) так, чтобы f1(x)M2(x)+f2(x)M2(x)=d(x), где d(x)-наибольший общий делитель f1(x) и f2(x):
f1(x)=x^4-4x^3+1, f2(x)=x^3-3x^2+1
Помогите пожалуйста, вообще не знаю что делать. Даже как начать :с
f1(x)=x^4-4x^3+1, f2(x)=x^3-3x^2+1
Помогите пожалуйста, вообще не знаю что делать. Даже как начать :с
понедельник, 02 февраля 2015
Простыми словами
25 января исполнилось 145 лет со дня рождения Нильса Фабиана Хельге фон Коха.

Википедия
Нильс Фабиан Хельге фон Кох (швед. Niels Fabian Helge von Koch, 25 января 1870 — 11 марта 1924) — шведский математик, брат композитора Сигурда фон Коха.
Родился в 1870 г. в Стокгольме. В 1887-1892 гг. учился в Стокгольмском институте, по завершении которого стал доктором философии и доцентом. В 1905 г. получил звание профессора математики при Технологическом институте, а в 1910 г. стал членом Шведской Академии наук.
Специалист преимущественно по теории чисел.
В статье «Об одной непрерывной кривой, не имеющей касательных...» (фр. Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire; 1904) впервые описал кривую Коха — один из самых ранних и самых известных примеров фрактала.
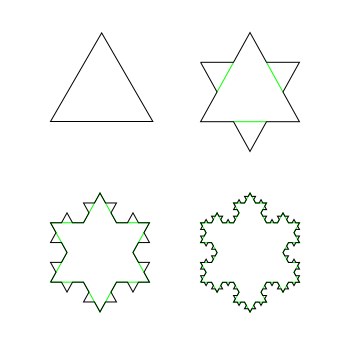
Кривая Коха и Снежинка Коха
Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом.
Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую бесконечной длины, называемую снежинкой Коха.
Кривая Коха
Построение
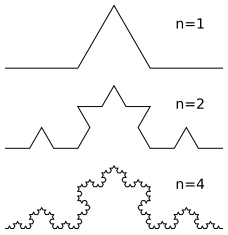
Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.
Свойства
Вариации и обобщения
Возможны обобщения кривой Коха, также использующие при построении подстановку ломаной из четырёх равных отрезков, но имеющей иную геометрию. Они имеют хаусдорфову размерность от 1 до 2. В частности, если вместо деления отрезка 1:1:1 использовать золотое сечение (φ:1:φ ), то получившаяся кривая имеет отношение к мозаикам Пенроуза.
Также можно построить кривую «Крест Коха» на сторонах квадрата, при этом проводя построение «внутрь» квадрата.
Также можно построить «Снежинку Коха» на сторонах равностороннего треугольника.
Вслед за подходом Коха были разработаны варианты с прямыми углами (квадратичная), других углов (Césaro) или кругов и их расширения на высшие размерности (сферическая снежинка).
Я покажу здесь только некоторые вариации. Посмотреть на остальные приглашаю в статью Википедии.

Фрактал Cesaro («Koch Curve 85degrees» участника Alexis Monnerot-Dumaine - Author. Под лицензией CC BY-SA 3.0 с сайта Викисклада)
Фрактал Cesaro — вариант кривой Коха с углом между 60° и 90 ° (здесь 85°).

Поверхность Коха («Koch surface 3» участника Robert Dickau - собственная работа. Под лицензией CC BY-SA 3.0 с сайта Викисклада)
Анимации
читать дальше
Ссылки и картинки
читать дальше

Википедия
Нильс Фабиан Хельге фон Кох (швед. Niels Fabian Helge von Koch, 25 января 1870 — 11 марта 1924) — шведский математик, брат композитора Сигурда фон Коха.
Родился в 1870 г. в Стокгольме. В 1887-1892 гг. учился в Стокгольмском институте, по завершении которого стал доктором философии и доцентом. В 1905 г. получил звание профессора математики при Технологическом институте, а в 1910 г. стал членом Шведской Академии наук.
Специалист преимущественно по теории чисел.
В статье «Об одной непрерывной кривой, не имеющей касательных...» (фр. Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire; 1904) впервые описал кривую Коха — один из самых ранних и самых известных примеров фрактала.
Кривая Коха и Снежинка Коха
Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом.
Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую бесконечной длины, называемую снежинкой Коха.

Кривая Коха
Построение
Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.
Свойства
- Кривая Коха нигде не дифференцируема и не спрямляема.
- Кривая Коха не имеет самопересечений.
- Кривая Коха имеет промежуточную (то есть не целую) хаусдорфову размерность, которая равна `ln4/ln3 approx 1,26` поскольку она состоит из четырёх равных частей, каждая из которых подобна всей кривой с коэффициентом подобия 1/3.
Вариации и обобщения
Возможны обобщения кривой Коха, также использующие при построении подстановку ломаной из четырёх равных отрезков, но имеющей иную геометрию. Они имеют хаусдорфову размерность от 1 до 2. В частности, если вместо деления отрезка 1:1:1 использовать золотое сечение (φ:1:φ ), то получившаяся кривая имеет отношение к мозаикам Пенроуза.
Также можно построить кривую «Крест Коха» на сторонах квадрата, при этом проводя построение «внутрь» квадрата.
Также можно построить «Снежинку Коха» на сторонах равностороннего треугольника.
Вслед за подходом Коха были разработаны варианты с прямыми углами (квадратичная), других углов (Césaro) или кругов и их расширения на высшие размерности (сферическая снежинка).
Я покажу здесь только некоторые вариации. Посмотреть на остальные приглашаю в статью Википедии.

Фрактал Cesaro («Koch Curve 85degrees» участника Alexis Monnerot-Dumaine - Author. Под лицензией CC BY-SA 3.0 с сайта Викисклада)
Фрактал Cesaro — вариант кривой Коха с углом между 60° и 90 ° (здесь 85°).

Поверхность Коха («Koch surface 3» участника Robert Dickau - собственная работа. Под лицензией CC BY-SA 3.0 с сайта Викисклада)
Анимации
читать дальше
Ссылки и картинки
читать дальше
Тигр, Тигр, жгучий страх, Ты горишь в ночных лесах. Чей бессмертный взор, любя, Создал страшного тебя?
Растолкуйте пожалуйста вкратце, в виде плана эдакого доказательство соответствующих теорем:
Теорема о перестановка членов абсолютно сходящихся рядов;
Теорема о перестановка членов условно сходящихся рядов(Теорема Римана);
З.Ы. Сами же доказательства достаточно большие, что и не запомнить.
Теорема о перестановка членов абсолютно сходящихся рядов;
Теорема о перестановка членов условно сходящихся рядов(Теорема Римана);
З.Ы. Сами же доказательства достаточно большие, что и не запомнить.
(2,6-m)^2 + (0.2-n)^2 = (m+3)^2 + (n-3)^2 - 39.2
(2,6-m)^2 + (0.2-n)^2 = (m-5)^2 + (n+1)^2 - 7.2
Раскрыл скобки, квадраты ушли.
Как правильно решить, чтобы не потерять решение?
Одно из них 0;-5
А вот другое потерял (5,2;5,4)
(2,6-m)^2 + (0.2-n)^2 = (m-5)^2 + (n+1)^2 - 7.2
Раскрыл скобки, квадраты ушли.
Как правильно решить, чтобы не потерять решение?
Одно из них 0;-5
А вот другое потерял (5,2;5,4)
воскресенье, 01 февраля 2015
Тигр, Тигр, жгучий страх, Ты горишь в ночных лесах. Чей бессмертный взор, любя, Создал страшного тебя?
Есть ли где краткое доказательство данного признака ?
суббота, 31 января 2015
Добрый вечер! Дана функция:`F(y) = int_0 ^1 ln(x^2+y^2)dx, Y={y: y != 0}`. Нужно исследовать функцию `F(y)` на непрерывность на множестве `Y`. Я взял в лоб интеграл, посмотрел, что проблемная точка только ноль, нашел левый и правый пределы и получил, что там разрыв первого рода (устранимый). Не подскажите, можно ли было как-то проще?
Нужно:
Атанасян Геометрия Лобачевского
Издательство: Просвещение
От производителя
В книге излагается геометрия Лобачевского на основе школьной аксиоматики абсолютной геометрии и аксиомы Лобачевского. Первая часть книги посвящена планиметрии Лобачевского, а вторая часть - стереометрии.
В конце каждой главы даются задачи, а в конце книги - ответы и указания к ним. Этим книга выгодно отличается от других пособий по геометрии Лобачевского.
Книга может с успехом использоваться в классах с углубленным изучением математики, для индивидуальной работы с учащимися, интересующимися математикой. Она также будет полезна студентам и преподавателям физико-математических факультетов университетов и педагогических вузов.

Где посмотреть?
Атанасян Геометрия Лобачевского
Издательство: Просвещение
От производителя
В книге излагается геометрия Лобачевского на основе школьной аксиоматики абсолютной геометрии и аксиомы Лобачевского. Первая часть книги посвящена планиметрии Лобачевского, а вторая часть - стереометрии.
В конце каждой главы даются задачи, а в конце книги - ответы и указания к ним. Этим книга выгодно отличается от других пособий по геометрии Лобачевского.
Книга может с успехом использоваться в классах с углубленным изучением математики, для индивидуальной работы с учащимися, интересующимися математикой. Она также будет полезна студентам и преподавателям физико-математических факультетов университетов и педагогических вузов.

Где посмотреть?
пятница, 30 января 2015
Сборник задач по геометрии в 2-х частях. Часть 2
Автор: Гусева Н.И., Денисова Н.С., Тесля О.Ю.
Название: Сборник задач по геометрии в 2-х частях. Часть 2
Издательство: КНОРУС
Год: 2012
Количество страниц: 529
Формат: Djvu
Размер: 5 Mb
rusfolder.com/42868556

Содержит задачи по проективной геометрии, методам изображений, элементам топологии, многогранникам, дифференциальной геометрии, основаниям геометрии, геометрии Лобачевского, площади и объему, неевклидовым геометриям. Также включает основные теоретические положения и примеры решения основных типов задач по каждому разделу и задачи второй части курса геометрии по специальностям: 032100 "Математика", 540200 "Физико-математическое образование (бакалавриат)", 510100 "Математика (бакалавриат)" и 031021 "Информатика".
Для студентов математических и физико-математических факультетов педагогических вузов. Может быть использовано для очных и заочных форм обучения, а также для организации самостоятельной работы студентов.
Автор: Гусева Н.И., Денисова Н.С., Тесля О.Ю.
Название: Сборник задач по геометрии в 2-х частях. Часть 2
Издательство: КНОРУС
Год: 2012
Количество страниц: 529
Формат: Djvu
Размер: 5 Mb
rusfolder.com/42868556

Содержит задачи по проективной геометрии, методам изображений, элементам топологии, многогранникам, дифференциальной геометрии, основаниям геометрии, геометрии Лобачевского, площади и объему, неевклидовым геометриям. Также включает основные теоретические положения и примеры решения основных типов задач по каждому разделу и задачи второй части курса геометрии по специальностям: 032100 "Математика", 540200 "Физико-математическое образование (бакалавриат)", 510100 "Математика (бакалавриат)" и 031021 "Информатика".
Для студентов математических и физико-математических факультетов педагогических вузов. Может быть использовано для очных и заочных форм обучения, а также для организации самостоятельной работы студентов.