Итоги студенческой олимпиады

[_ТошА_]

Итоги студенческой олимпиады

Итак, наконец-то собравшись с силами и со временем, спешу поделиться с вами результатами олимпиады, проводившейся не так давно.
В целом, участники порадовали, не порадовало одно - многие из записавшихся не участвовали - так ни по одной задаче и не выложили. Но, это их право.
Представлю вам оргкомитет олимпиады:
 VEK,  Alidoro,  Heor,  _ТошА_
К вышеперечисленным можно обращаться по всем вопросам оценивая и проч. в комментариях записи.
Конечно нельзя забыть  Robot, которая хоть формально и не числится в оргкомитете из-за лишней скромности, но очень-очень нам помогала, без неё ничего бы не вышло.
Ну и, собственно, результаты:
1 место -  Alisa_Selezneva
2 место -  vyv2
3 место -  Mist*,  nvse
Так же участвовал школьник, абсолютно верно решивший одну задачу:  Rus-Kira

Поздравляем их с очень хорошим выступлением! У всех были очень интересные решения, спасибо!

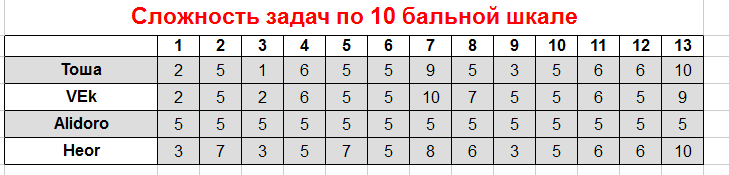
Теперь немного про оценивание. Сначала о таком параметре, как сложность задач.
Каждый проверяющий выставил свой балл каждой задаче - от 0 до 10 в порядке увеличения сложности (10 - очень сложная, 0 - элементарная).
Вот таблица, показывающая распределившиеся баллы сложности по задачам:

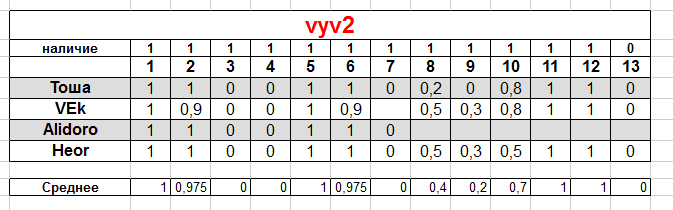
За задачу каждый участник получал от 0 до 1 балла. Затем бралась средняя оценка из выставленных. Не все проверяющие поставили баллы по всем задачам: причины различны. Таблицы выставленных оргкомитетом баллов:

Alisa_Selezneva

Mist*

vyv2

nvse

Собственно, баллы пересчитывались вот по какой формуле:
Расчёт коэффициента сложности k = (среднее арифметическое сложностей, выставленных оргкомитетом)*(количество участников)/(5*(количество решивших))
Количество баллов по i-ой задаче, выставленных участнику:
n = (среднее арифметическое из оценок, выставленных оргкомитетом)*`k_i`

И сама таблица баллов:



А теперь решения от составителей:
1) Решить в `ZZ`: `3x^2 - 7xy +2y^2 + 19x - 18y = -35`
Решение:
Перепишем в виде `3x^2-7xy+2y^2+19x-18y+28=-7`
Рассмотрим левую часть как квадратный трехчлен относительно `х`
`f(x)=3x^2-x(7y-19)+2y^2-18y+28`
Тогда `x_(1,2)=((7y-19)+-5(y-1))/6`
Откуда `x_1=(12y-24)/6=2y-4`
`x_2=(2y-14)/6=(y-7)/3`
`3x^2-x(7y-19)+2y^2-18y+28=(x-2y+4)(3x-y+7)`
Уравнение принимает вид
`(x-2y+4)(3x-y+7)=-7`
Рассматривая совокупность четырех систем, имеем две пары решений
`(1;3)` и `(-5;-1)`
Ответ: `(1;3)` и `(-5;-1)`


2) Найти сумму:
`cos(x) + C_n^1cos(2x) + ... + C_n^ncos((n+1)x)`
Решение:


3) Найти функцию `f(x)` `x in (0, 1)`, если `f'(sin^2(x)) = cos(2x) + tg^2(x)`
Решение:
`f'(sin^2(x)) = 1 - 2sin^2(x) + (sin^2(x))/(1 - sin^2(x))`
`f'(t) = 1 - 2t + t/(1 - t) = 1 - 2t - 1 + 1/(1 - t) = -2t + 1/(1 - t)`
`f(t) = -t^2 - ln|1 - t| + C`
Ответ: `f(t) = -t^2 - ln|1 - t| + C`


4) Пусть `t` - дифференцируема на `[a, b]` функция, `t(a) = t(b) = 0`. Доказать, что существует `c in (a, b): t(c) = t '(c)`
Решение:
Составим функцию `g(x) = t(x)*e^(-x)`
`g(a) = g(b) = 0` и g дифференцируема на (a, b)
Тогда по теореме Ролля существует `c in (a, b): g'(c) = 0`
`g' = t'(x)e^(-x)-t(x)e^(-x)`
`g'(c) = t'(c)e^(-c) - t(c)e^(-c) = 0 => t'(c) = t(c)`

5) Пусть `f` - бесконечно дифференцируемая функция. Решить функциональное уравнение: `f(x+y) = f(x) + f(y) +xy(x^2/3 + xy/2 + y^2/3)`, зная что `f(2) = -2`
Решение:
Продифференцируем функцию по y
`f'(x+y) = f'(y) + x(x^2/3 +xy/2 + y^2/3) + xy(x/2 + 2y/3)`
Пусть y = 0
`f'(x) = C_1 + x^3/3`
`f(x) = C_1x + x^4/12 + C_2`
заметим, что `f(0 + 0) = f(0) + f(0) = 2f(0) => f(0)=0`
`f(x) = C_1x + x^4/12`
Найдём `C_1`
`-2 = 2C_1 + 4/3`
`C_1 = -5/3`
Ответ: `f(x) = -5/3x + x^4/12`

6) Решить функциональное уравнение: `2xf(x) + f(1/(1-x)) = 2x`
Решение:
`2xf(x) + f(1/(1-x)) = 2x`
`] t = 1/(1-x)`
`x = (t-1)/t`
Уравнение:
`2*(t-1)/t*f((t-1)/t) + f(t) = 2(t-1)/t`
`] t = (p-1)/p`
`-2/(p-1)*f(1/(1-p)) + f((p-1)/p) = -2/(p-1)`
`] f(x) = a, f(1/(1-x)) = b, f((x-1)/x) = c`

Система:
`2xa + b = 2x`
`2(x-1)/xc + a = 2(x-1)/x`
`-2/(x-1)b + c = -2/(x-1)`

`a = (6x - 2)/(7x)`
Ответ: `f(x) = (6x - 2)/(7x)`

7) `x_1 in (0, 1)` `x_(n+1) = ln(1 + x_n)` Найти `lim_(n->oo) n*x_n`
Решение:
`x_1 in (0, 1)`
`x_(n+1) = ln(1 + x_n)`
Найти `lim(nx_n)`
`x_2 = ln(1 + x_1) < x_1`
`x_3 = ln(1 + x_2) < x_2 < x_1`
Продолжая по индукции получим, что `{x_n}` убывает. Она ограничена снизу нулём, значит по т. Вейерштрасса имеет предел.
`l = ln(1 + l)`
`e^l = 1 + l`
`l = 0`

Итак, последовательность стремится к нулю.

Рассмотрим `1/x_n`

`1/(x_n) = 1/(ln(1 + x_(n - 1))) = 1/(x_(n - 1) - (x_(n-1))^2/2 + o((x_(n-1))^2)) = `
`= 1/x_(n - 1)(1 - (x_(n-1))/2 + o(x_(n-1)))^(-1) = 1/x_(n-1)(1 + x_(n-1)/2 + o(x_(n-1))) = 1/(x_(n - 1)) + 1/2 + o(1)`
Распишем сумму:
`1/x_n = 1/x_0 + 1/2n + o(1) + .. + o(1)`
`x_n = 1/(1/x_0 + 1/2n + o(1) + ... + o(1))`
`lim nx_n = 2`
Ответ: 2

8) Вычислить: `lim_(n->oo) ((n+1)ln(n!) - 2ln(2!3!...n!))/(n^2)`
Решение:
2 раза Штольца
`lim_(n->oo) [(n+1)ln(n!) - 2ln(2!*3!*..*n!)]/(n^2) = lim_(n->oo) [(n+1)ln(n!) - 2ln(2!*3!*..*n!) - nln((n-1)!) + 2ln(2!3!...(n-1)!)]/(n^2 - (n-1)^2) = `
` = lim (nln(n) - ln(n!))/(2n-1) = lim [nln(n) - ln(n!) - (n-1)ln(n-1) + ln((n-1)!)]/(2) = lim [nln(n/(n-1)) + ln(n-1) - ln(n!) + ln((n-1)!)]/2 = `
`= lim [nln(n/(n-1)) + ln(n-1) - ln(n)]/2 = lim (nln(1 + 1/(n-1)) + ln(1 - 1/n))/2 = lim (n(1/(n - 1) + o(1/(n-1))) + 0)/2 = 1/2`
Ответ: 1/2

9) Вычислить: `int_(-1)^1 (ln(1+x^2))/(1+e^x)dx`
Решение:
`I = int_(-1)^0 (ln(1+x^2))/(1+e^x)dx + int_(0)^1 (ln(1+x^2))/(1+e^x)dx = int_(0)^1 (ln(1+x^2)e^x)/(1+e^x)dx + int_(0)^1 (ln(1+x^2))/(1+e^x)dx = `
`= int_0^1 ln(1+x^2)dx = ln2 - 2 + pi/2`
Ответ: `ln2 - 2 + pi/2`

10) Найти общее решение диф. уравнения: `(x^2 + 1)((y')^2 - yy'')= xyy'`
Решение:
`y = 0` - решение. Пусть `y!=0`
`-(x^2 + 1)((y')/y)' = x(y')/y`
`] t = (y')/y`
`t' = -xt/(x^2 + 1)`
`ln|t| = -1/2ln|x^2 + 1| + C_1`
`t = C_1/(sqrt(x^2 + 1))`
`(y')/y = C_1/(sqrt(x^2 + 1))`
`ln|y| = C_1*ln|x + sqrt(x^2 + 1)| + C_2`
`y = C_2*(x+sqrt(x^2 + 1))^(C_1)`
`C_1, C_2 in RR`
Ответ: `y = C_2*(x+sqrt(x^2 + 1))^(C_1)`


11) Найти общее решение диф. уравнения: `y' = y/(y^2 + 1)(1/x + ye^x - y^2/x)`
Решение:
`y = 0` - решение. Пусть `y!=0`.
`(y+1/y)dy = (1/x + ye^x -y^2/x)dx`
поделим ещё на y
`(1 + 1/y^2)dy = (1/x(1/y - y) + e^x)dx`
`t = (y - 1/y)`
`dt = 1 + 1/y^2`

`dt = (-1/xt + e^x)dx`
`t' = -t/x + e^x`
`(dt)/(dx) = -t/x`
`ln|t| = ln|c/x|`
`t = c/x`
`t' = (c')/x - c/x^2`
`(c')/x = e^x`
`c' = x*e^x`
`c = int xe^xdx = xe^x - e^x + C`
`t = (xe^x - e^x + C)/x`
`y - 1/y = (xe^x - e^x + C)/x`
`C in RR`

Ответ: `y - 1/y = (xe^x - e^x + C)/x`, `y = 0`

12) Параметры `a` и `b` меняются так, что система
`{(y = ax + 1), (x^2 + y^2 = 2bx):}`
имеет единственное решение `(x_0, y_0)`. Какую кривую при этом описывает точка `M_0(x_0, y_0)`?
Решение:
Геометрическая интерпретация 1-го уравнения - прямая , проходящая через точку (0;1), геометрическая интерпретация второго уравнения окружность с центром в точке в точке `(b;0)` и радиусом `|b|`. Нужна картинка.
Пусть `b > 0`. Прямая имеет с окружностью единственную общую точку тогда и только тогда , когда она ее касается. Поскольку точка (0;1) расположена вне указанной окружности при любом значении параметра b, то прямая и окружность должны иметь 2 точки касания. Одна из них - точка (0;0), но через не проходит касательная `x=0`, что противоречит условию.
Найдем координаты второй точки касания. Имеем: `{(sqrt(2bx-x^2)=ax+1),((b-x)/sqrt (2bx-x^2)=a):}`. Отсюда `x=(b-a)/(a^2+1)`, и подставляя это значение в любое уравнение, получаем `(ab+1)=sqrt((b-a)(2b(a^2+1)-(b-a)))`, откуда `(a^2+1)(2ab-b^2+1)=0`. Значит параметры (a и b при касании прямой и окружности связаны соотношением`a=(b^2-1)/(2b)` .
Координаты точки касания `(x_0;y_0)=((2b)/(b^2+1); (2b^2)/(b^2+1))`. Исключим параметр `b` для уравнения связи, имеем `b^2=y/(2-y)`, тогда `x=sqrt(2y-y^2)` или `x^2+(y-1)^2=1` (правая полуокружность).
Пусть `b<0`, тогда все решение повторяется,за исключением последней строки: `x=-sqrt(2y-y^2)` и значит получаем вторую полуокружность.
Теперь окончательный ответ: точка M движется по окружности `x^2+(y-1)^2=1`
На окружности имеются 2 выколотые точки: (0;0) и (0;2).
Ответ: `x^2+(y-1)^2=1` На окружности имеются 2 выколотые точки: (0;0) и (0;2)

13) Пусть `a_1 < a_2 < ... < a_k <= n`, - такой конечный набор натуральных чисел, наименьшее кратное любых двух из которых больше `n`. Доказать, что `sum_(i=1)^k 1/a_i < 2`
Решение:
Пусть `a_1=1`, тогда в наборе только одно число и утверждение задачи очевидно.
Пусть `a_1 >= 2`. Обозначим `b_m` – число элементов конечного набора `{a_1,a_2,…,a_k}`, удовлетворяющих неравенствам `(m-1)/n <= 1/a_i < m/n`, `m=2,3,…,n+1` (1).
Каждый из этих `b_m` элементов `a_i` имеет `(m-1)` кратных среди `n` первых (без единицы) натуральных чисел, причем никакие два из этих элементов не имеют общего кратного среди `n` первых натуральных чисел. Таким образом, `b_2+2b_3+3b_4+⋯+nb_(n+1)=sum_(m=2)^(n+1) (m-1)b_m = n - r_1`, `r_1 >=0`. (2)
Для любого конечного набора `a_1 < a_2 < ⋯ < a_k` мы можем, не ограничивая общности, выбрать `n=a_k`. Тогда, как следует из неравенства (1) (`1/a_k =1/n`, это число входит в количество элементов `b_2`, выделяем его),
`sum_(i=1)^k 1/a_i < 1/n + (b_2-1)*2/n + b_3*3/n + b_4*4/n + ⋯ + b_(n+1)*(n+1)/n = -1/n + sum_(m=2)^(n+1) m/n b_m = 1/n(-1+sum_(m=2)^(n+1) mb_m)`.
Подставляя значение `b_2 = n-r_1-sum_(m=3)^(n+1) (m-1)b_m` из соотношения (2), получаем
`sum_(i=1)^k1/a_i < 1/n(-1+2b_2+sum_(m=3)^(n+1) mb_m) = 2-1/n-(2r_1)/n - 1/n(sum_(m=3)^(n+1) (m-2)b_m)`, что и доказывает неравенство `sum_(i=1)^k 1/a_i < 2`.

Замечание. Оценка может быть улучшена: `sum_(i=1)^k 1/a_i <6/5`.

@темы: Тренинги eek

---

Исследовать на лин.зависимость сист.функций (БОЛЬШАЯ КАРТИНКА)

[Temik2704]

Исследовать на линейную зависимость систему функций
(1,`lg10t^3`,`lg(100/t^2)`)



По определению следует,что если определитель,равен нулю,для любого Х на отрезке (а;b),то это еще не означает что f1,f2...fk (из которых состоит система) - линейно зависимые.

Спрашивал у преподавателя,он ответил,что надо выразить одно через другое (что именно и как я не расслышал)
Не могли бы вы подсказать порядок действий выражения "одного через другое"?

---

[gyaskevich]

нужно показать, что функция `z=ln(1/sqrt(x^2-y^2))` удовлетворяет заданному уравнению `(d^2z)/dx^2+(d^2z)/dy^2=0`. после нахождения производных второго порядка получаются одинаковые слагаемые `(x^2+y^2)/(x^2-y^2)^2`, которые в сумме не могут дать ноль. проверьте пожалуйста

---

Математический тренинг по части С (ЕГЭ по математике)

[Robot]

Дорогие друзья!

24 марта в 23-59 закончилась студенческая олимпиада, о результатах которой будет объявлено несколько позже

А теперь новое объявление!

Оно должно было появиться чуть раньше, но я думала, что его вывесит Тоша, а Тоша думал, что я=(

Как мы и обещали, в скором времени пройдёт математический тренинг по части С для школьников 10-11 классов.
Состоится сие действо в воскресенье, 27.03.2011, в 13 часов по московскому времени (время индивидуально). (Не забываем, ночью, в 2 часа, 27 марта переводятся часы на 1 час вперёд).
Продолжительность олимпиады - 5 часов. Регистрация заранее, запись в комментариях.
Будем надеяться, что все те, кто хотел участвовать, успеют прочесть, настроиться и освободить время в воскресенье.
Напоминаю то, о чем писал Тоша в прошлый раз:
Специально для математических соревнований был создан дневник olympeek, который можно найти по адресу: www.diary.ru/~olympeek/
В комментариях к данной записи Вы пишете о своем желании участвовать в тренинге по части С.
Создаётся запись, закрытая для всех, кроме вас и оргкомитета. В этой записи вы и будете выкладывать решения.
Про формат:
Он может быть любым: сканы ваших решений, фотографии, текст+ формулы в формате скрипта. Главное - чтобы можно было понять что и как, а не ломать глаза и не гадать.
P.S.
Если вдруг пожелают поучаствовать в этом учителя и преподаватели, милости простим! Только, простите, конкурс будет отдельным. Поэтому в заявках просьба указывать класс (10 или 11) или тот факт, что Вы уже закончили школу.
P.P.S. Запись будет время от времени подниматься

UPD
.
На данный момент зарегистрированы
Oleg7351 (11 класс) www.diary.ru/~olympeek/p152516567.htm
FirstAID (10 класс) www.diary.ru/~olympeek/p152515232.htm
logarithm (11 класс) www.diary.ru/~olympeek/p152515637.htm
Новый гость (11 класс) www.diary.ru/~olympeek/p152514803.htm
orbit13 (11 класс) www.diary.ru/~olympeek/p152516834.htm
дочка Гостя (10 класс) www.diary.ru/~olympeek/p152516297.htm
Rus-Kira (11 класс) www.diary.ru/~olympeek/p152518052.htm
Dragonway (11 класс) www.diary.ru/~olympeek/p152531093.htm
bmi (11 класс) www.diary.ru/~olympeek/p152538788.htm
Zykloned (11 класс) www.diary.ru/~olympeek/p152569682.htm
asymptote (11 класс) www.diary.ru/~olympeek/p152576807.htm
quest_ (10 класс) www.diary.ru/~olympeek/p152577800.htm
X-Rain (11 класс) www.diary.ru/~olympeek/p152599703.htm

Upd2

Для использования скрипта в дневнике www.diary.ru/~olympeek/ можно

1. Добавить в скрипт своими руками адреса

// @include       http://*.diary.ru/*
// @include       http://diary.ru/*

или

2. Установить модифицированную версию скрипта asciimathml.narod2.ru/display-latex6x.user.js (она работает для всех дневников, сообществ diary.ru)

UPD3
В случае невозможности выложить решение в своем топике (падение diary или еще какие-то глобальные проблемы) можно отправить файлы на электронный адрес [email protected]

запись создана: 25.03.2011 в 00:54

@темы: Тренинги eek

---

Исследовать функцию на экстремум

[alligator76]

Необходимо исследовать функцию двух переменных `u(x,y)` на экстремум:

`u=1+y^2-root(5)((x-2)^4)`

Применяя необходимое условие экстремума функции двух переменных, нахожу стационарные точки:

`u'_x=-(4(x-2)^3)/(5*root(5)((x-2)^8))=-(4/5)*(x-2)^(7/5)=0`
`u'_y=2y=0`

Нахожу точку (2,0)

Затем применяю достаточное условие экстремума, нахожу вторые частные производные:

`u''_(xx) =-(28/25)*(x-2)^(2/5)`
`A=u''_(xx) (2,0)=0`

`u''_(xy) =0`
`C=u''_(xy) (2,0)=0`

`u''_(yy) =2`
`B=u''_(yy) (2,0)=2`

Нахожу `D=AB-C^2=0`.

Следовательно, необходимы дальнейшие исследования.

Какие дальнейшие исследования можно сделать в моем случае?

@темы: Математический анализ, Исследование функций

---

Статистика

[krazy]

Здравствуйте!
Не могли бы вы подсказать литературу для решения задач подобного типа:

Используя данные о расходовании ресурсов со склада, представленные в таблице, определить время принятия решения о пополнении запасов в условиях работы в рамках «s-S» системы (s =45; S =120). Предусмотреть возможное изменение параметров работы системы в случае необходимости. Заполнить аналитическую таблицу принимаемых решений и показать изменение уровня запасов графически. Условия работы склада – непрерывная 5-ти дневная рабочая неделя (1-е число – вторник!)
(Далее дана таблица - период времени и расход ресурса)
Заранее огромное спасибо!!!!

@темы: Математическая статистика

---

Смирнова И.М., Смирнов В.А. Геометрия 10-11

[Ak-sakal]

Смирнова И.М., Смирнов В.А. Геометрия 10-11. Базовый и профильный уровни Предлагаемый учебник двухуровневый: с учетом параграфов со звездочкой он соответствует профильному уровню, без их учета - базовому. Наряду с традиционными вопросами геометрии пространства в качестве дополнительного в учебник включен материал научно-популярного и прикладного характера, а также помещены нестандартные и исследовательские задачи, исторические сведения. Большое внимание уделено использованию средств наглядности: изображению пространственных фигур, различным способам их моделирования; приведены соответствующие рисунки, чертежи, модели, иллюстрации, компьютерная графика. Данный учебник концептуально согласуется с учебниками по алгебре и началам анализа А. Г. Мордковича. Скачать (djvu, 8.07 Мб) Возможность скачивания данного файла заблокирована по требованию правообладателя.

@темы: Стереометрия, Литература

---

Определенный интеграл

[Zagrebatel]

Определить площадь меньшей из фигур, ограниченных линиями r=4*cos(fi); r=3/cos(fi)
fi - угол. Проблема в построении фигур не могу понять как строятся фигуры в декартовой системе координат, помогите пожалуйста

@темы: Интегралы, Высшая алгебра

---

Непрерывность ф-ии

[Deceember]

я обычно доверяю учебникам но в этом случае я просто не понимаю откуда там такой ответ

Есть ф-ия 2х переменных

u=(x^2+y^2)/2x при x неравном 0
u=0 при x=0

Надо опрелить непрерына ли она

Ищем предел Lim((x^2+y^2)/2x) при x->0 y->0 получаем что он равен 0 равен значению фу-ии в предельной точке значит ф-ия непрерывна, а в ответе написано что нет. кто прав я или книжка

Заранее спасибо за помощь.

---

Подскажите пожалуйста!

[sunday24]

Как получить из arccos(1-sqrt(2)) 3*pi/4?
Или может, если проще, из 2*arcctg(sqrt(2)-1) тот же ответ 3*pi/4?

@темы: Тригонометрия

---

Помогите, пожалуйста, разобраться!

[Phaust94]

Здравствуй, любимое сообщество. Такая ситуация: занялся я на досуге изучением топологии, скачал книжку Болтянского "Наглядная топология". Есть пара вопросов:
1)Теорема Эйлера (Эйлерова характеристика конечного связного графа, вычерченного на сфере, грани которого гомеоморфны кругу, равна двум (В-Р+Г=2, где В-вершины, Р-рёбра, Г-грани)). Есть проблема с доказательством: мы выбираем максимальное дерево графа (почему максимальное, ведь оно, вроде, определено однозначно с точностью до различных рёбер, но число их постоянно), и говорим, что для него верно, т.к. (В-Р) дерева равно 1 , получается, что остаётся одна грань. какая грань остаётся, если это дерево? Ведь грань по определению гомеоморфна окружности.
2) можно ли достать эту книгу на английском где-нибудь, в электронном, разумеется, варианте?

Второй вопрос в силе!

Примечание Robot: Поднимаю

запись создана: 24.03.2011 в 18:20

@темы: Поиск книг, Теория графов

---

Подскажите, как исследовать на сходимость вот такой функциональный ряд?

[roches]

Подскажите, как исследовать на сходимость вот такой функциональный ряд?
$\sum_{n=1}^{\infty}$ `ln(1+x^2/n^3)`
на равномерную сходимость на промежутке $-\infty < x < +\infty.
с помощью признака Вейерштрасса ведь можно? Незнаю как к нему подобраться...

@темы: Математический анализ, Ряды

---

Задачка

[ritmix10]

Всем Привет))!

Такая вот задачка
Найти экстремальные значения функции `u=x^2/a^2+y^2/b^2+z^2/c^2` если у нее есть два уравнения связи
`x^2+y^2+z^2=1`
`xcosA+ycosB+zcosY=0`
и условие `x,y,z>0; cos^2(A)+cos^2(B)+cos^2(Y)=1`
составил функцию Лагранжа
взял частные производные:

`(dL/dx)=(2x/a^2)+2xl_1+l_2cosA=0`
`(dL/dy)=(2y/b^2)+2yl_1+l_2cosB=0`
`(dL/dz)=(2z/c^2)+2zl_1+l_2cosY=0`
`(dL/dl_1)=x^2+y^2+z^2-1=0`
`(dL/dl_2)=xcosA+ycosB+zcosY=0`

что сделать дальше
понятно что нужно получить `x,y,z l_1 l_2`

@темы: Математический анализ

---

Маленький вопрос

[Vzzzz!]

Существует ли какой-нибудь критерий замкнутости кривой F(x,y) = 0 ?

@темы: Функции

---

Помогите срочно по геометрии.До завтра нужно.

[marik2000]

Три задачки:
Боковое ребро правильной четырехугольной призмы равно 12 см.Диагональ боковой грани составляет с плоскостью основания угол 60 градусов.Найти диагональ основания, площадь поверхности призмы, объем описанного цилиндра, площадь сечения призмы плоскостью, проходящей через стороны одного основания и среднюю линию другого основания.

Из цилиндра вырезан конус, основание которого совпадает с одним из оснований цилиндра, а вершина--с центром другого основания.Высота цилиндра 6 см, диаметр основания 20 см.Найдите объем полученного тела и площадь его поверхности.

Сколько краски пойдет на покрытие 100 деревянных шаров диаметром 10 см, если на 1 квадратный дм поверхности затрачивается 1,22 г краски?

Чертежи ОЧЕНЬ ЖЕЛАТЕЛЬНЫ.Всем спасибо за помощь.

@темы: Планиметрия

---

Производные 1 курс

[Лучик искренности]

Пожалуйста, помогите найти две производные.

Первая(насколько я поняла, задана в неявном виде):

y*sin(x+y)-x=0

Вторая(задана параметрически):

система: x=cos t+t*sin t

y=sin t -t*cos t

Не обязательно решать, просто объясните мне алгоритм, что делать нужно. Во второй, наверное, найти от каждого производную, а дальше что?

@темы: Производная

---

Лысенко.Математика ЕГЭ 2009

[Shadow_Cat]

тема:логарифмические и паказательные уравнения.
не могу решить два задания по данной теме,подскажите пожалуйста.
1.найдиите значение аргумента х,при котором значения функций `y=3^(x+2)-7*3^(x-1)`;`y=3^x+2*3^(x+1)-3` равны
в этом заданиии я пыталась вынести общий множитель
сначала перенесла все в одну сторону ,кроме 3
затем вынесла` 3^(x-1)` в скобках упростила и получила
`-3^(x-1)=3`
и тут застряла..
2.найдите значение переменной х,при котором разность чисел `2^x `и `2^(1-x)` равна 1

@темы: ЕГЭ

---

Помогите пожалуйста с решением лин. алгебры и ан.геометрии(2 семестр)

[isuh]

Линейный оператор с в пространстве v3 есть последовательное применение лин. операторов а и b найти матрицы операторов а b c в базисе i j k обратим ли оператор с? если да, то описать его геометрическое действие

оператор а - проектирование на плоскость xoz

оператор b - векторное умножение на вектор а = i+j-k

@темы: Линейная алгебра, Аналитическая геометрия

---

Помогите, пожалуйста. Задача 10 класс.

[_*Kristina*_]

Тут уже решалась эта задача (2 года назад), но я так и не поняла, откуда и что взялось.

Трактовка:

Основание прямой призмы - равнобедренный треугольник с боковой стороной 6 и углом при вершине 120 градусов. Диагональ наибольшей боковой грани образует с плоскостью основания призмы угол 60 градусов. Найти площадь боковой грани и полной поверхности призмы.

@темы: Стереометрия

---

Помогите решить задания B

[Life11]

B4
В треугольнике ABC AC=BC, AB=8, sinA=3/5. угол H=90 градусов . Найдите высоту CH

B7
Найти значение выражения
-4sin26*/sin334*
*-градусы

И вот ещё B12, почти решил, но чего-то не получается.

первая труба наполняет резервуар на 55 мин дольше, чем вторая. Обе трубы наполняют это же резервуар за 24 мин, за сколько мин наполняет этот резервуар одна вторая труба ?


(x+55)*x=24
x^2+55x-24=0
Получается корень из 3121, а такого как раз нет или может я где-то ошибся...

@темы: ЕГЭ