пятница, 10 июля 2015
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
вторник, 07 июля 2015
нормально делай нормально будет.
Пусть `x_1 x_2 cdots x_n` – выборка случайной величины X.
Является ли статистика `Z=1/2*x_1+1/(2n-2)*sum_(k=2)^n x_k` асимптотически несмещенной оценкой EX ?
Первый раз вижу такую задачу и понятия не имею, что такое асимптотически несмещенная оценка. Подскажите, как решать и может есть у вас пара подобных задач для тренировочки?
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
пятница, 03 июля 2015
I think its gonna rain
Здравствуйте.
Подскажите, что можно почитать про использование диаграмм Эйлера-Венна в логике предикатов? Ничего конкретного не гуглится.
Подскажите, что можно почитать про использование диаграмм Эйлера-Венна в логике предикатов? Ничего конкретного не гуглится.
Если в многошаговых методах численного решения ОДУ не выполняется условие нормировки коэффициентов, то это влияет на устойчивость? Или вообще может такое быть, чтоб в этом классе методов не выполнялось условие нормировки коэффициентов?
Торопись жить.
Известны данные по урожайности пшеницы по 101 ферме. Среднее значение mu = 15 бушелей с акра, стандартное отклонение - 4 бушеля. Найти вероятность того, что в выборке из 25 ферм выборочное среднее будет меньше или равно 13,5 бушелей.
Решаю задачи по задачнику, из названия темы ясно, что надо решать через центральную предельную теорему. Но пока не знаю как и не могу найти похожие разобранные задачи. Подскажите, пожалуйста, решение и какой-нибудь учебник или ресурс типа Вентцеля, где есть разобранные задачи по этой теме (идеально, если по матстатистике в целом).
Решаю задачи по задачнику, из названия темы ясно, что надо решать через центральную предельную теорему. Но пока не знаю как и не могу найти похожие разобранные задачи. Подскажите, пожалуйста, решение и какой-нибудь учебник или ресурс типа Вентцеля, где есть разобранные задачи по этой теме (идеально, если по матстатистике в целом).
четверг, 02 июля 2015
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
нормально делай нормально будет.
Условие:
` y'=(2y+1)*ctgx`Если где-то неправильно взят интергал или есть другая ошибка - то ладно, а если все верно - то arctg меня пугает и я не могу выразить у.
нормально делай нормально будет.
Найти предел.
`lim_(x->0)((1+3x+2x^2)/(1-2x-x^2))^(-2/x^2) `нормально делай нормально будет.
При возведении функции с ограничениями (например при х>n y=чему-нибудь) в степень, ограничения тоже возводятся в степень? А если одно из ограничений с отрицательным числом?
вторник, 30 июня 2015
Апелляционный суд Англии и Уэльса выдвинул правовое определение единице: это число, значение которого больше или равно 0,5 и меньше 1,5. Это решение было вынесено во время разрешения патентного спора между фармацевтическими компаниями ConvaTec и Smith & Nephew, сообщает The Independent.
«Цифры, не в меньшей степени, чем слова, меняют смысл в зависимости от контекста. Для лингвиста "единица" означает единицу, не более и не менее. Но в определенном контексте оно может отсылать к значениям, выходящим за пределы целого числа», — заявил лорд-судья Кристофер Кларк (Christopher Clarke).
Судебное дело было вызвано апелляцией компании ConvaTec на решение по патентному спору, в результате которого действие ее патента было признано в отношении лекарств с концентрацией серебра от 0,95 процента до 25,5 процента. Из-за этого конкурирующая фирма Smith & Nephew, в лекарстве которой применялся 0,77-процентный раствор, получила право получать многомиллионные прибыли, ничего не выплачивая ConvaTec.
Решение суда первой инстанции было принято в 2013 году, исходя из правила округления с учетом количества значащих цифр (все числа меньше 0,95 округлялись до десятых: 0,9, 0,8 и так далее). Однако компания ConvaTec обратила внимание судей высшей инстанции на странную асимметрию в первом решении: разница между минимальным значением до целого числа почти в десять раз меньше, чем между максимальным и ближайшим целым. Для исправления этой асимметрии Апелляционный суд учел операцию округления и постановил, что единице соответствует все, что больше или равно 0,5 и меньше 1,5. Таким образом, 0,77-процентный раствор Smith & Nephew теперь попадает под действие патента ConvaTec.
Фирма ConvaTec запатентовала антисептический раствор с содержанием серебра. Патент покрывал любой раствор, содержащий от 1 до 25 процентов всего объема лекарственного средства. Компания Smith & Nephew создала конкурирующий продукт с концентрацией в 0,77 процента.
«Цифры, не в меньшей степени, чем слова, меняют смысл в зависимости от контекста. Для лингвиста "единица" означает единицу, не более и не менее. Но в определенном контексте оно может отсылать к значениям, выходящим за пределы целого числа», — заявил лорд-судья Кристофер Кларк (Christopher Clarke).
Судебное дело было вызвано апелляцией компании ConvaTec на решение по патентному спору, в результате которого действие ее патента было признано в отношении лекарств с концентрацией серебра от 0,95 процента до 25,5 процента. Из-за этого конкурирующая фирма Smith & Nephew, в лекарстве которой применялся 0,77-процентный раствор, получила право получать многомиллионные прибыли, ничего не выплачивая ConvaTec.
Решение суда первой инстанции было принято в 2013 году, исходя из правила округления с учетом количества значащих цифр (все числа меньше 0,95 округлялись до десятых: 0,9, 0,8 и так далее). Однако компания ConvaTec обратила внимание судей высшей инстанции на странную асимметрию в первом решении: разница между минимальным значением до целого числа почти в десять раз меньше, чем между максимальным и ближайшим целым. Для исправления этой асимметрии Апелляционный суд учел операцию округления и постановил, что единице соответствует все, что больше или равно 0,5 и меньше 1,5. Таким образом, 0,77-процентный раствор Smith & Nephew теперь попадает под действие патента ConvaTec.
Фирма ConvaTec запатентовала антисептический раствор с содержанием серебра. Патент покрывал любой раствор, содержащий от 1 до 25 процентов всего объема лекарственного средства. Компания Smith & Nephew создала конкурирующий продукт с концентрацией в 0,77 процента.
Расширен перечень материалов, ссылки на которые не нужно публиковать в сообществе. Подробности в этом топике.
понедельник, 29 июня 2015
Р. Смаллиан. Шахматные тайны. 100 труднейших задач, связанных с расследованиями в области шахмат. Пер. с английского П. Быстров. М.: «Канон +», 2012.- 240 с.
В издании представлены две книги задач по ретроспективному анализу шахматной игры, изобретенных Р.М. Смаллианом, логиком, философом и музыкантом. Эти книги объединяет не только древняя игра, любимая миллионами людей, но и глубокий анализ логических методов построения рассуждений. Автор с большим литературным мастерством показывает, как решают интеллектуальные головоломки Шерлок Холмс с доктором Ватсоном, и описывает увлекательные приключения живых шахматных фигур в мире заколдованных замков, джинов и прочих чудес. Такие книги не просто интересно читать, они увлекают, возбуждают желание проверить свои возможности в ситуациях, в которых нужно мыслить строго логически и в то же время творчески, нестандартно.
Примечание сканировщика: в книге исправлены многочисленные орфографические ошибки, а также (не такие многочисленные) опечатки на диаграммах и в тексте решения задач.
Еще один отзыв: vk.com
P.S. The Chess Mysteries of Sherlock Holmes и The Chess Mysteries of the Arabian Knights можно найти в сети.
P.P.S. Как лучше перевести такой фрагмент:
Haroun Al Rashid --- The White king
Amelia --- His queen
?
В издании представлены две книги задач по ретроспективному анализу шахматной игры, изобретенных Р.М. Смаллианом, логиком, философом и музыкантом. Эти книги объединяет не только древняя игра, любимая миллионами людей, но и глубокий анализ логических методов построения рассуждений. Автор с большим литературным мастерством показывает, как решают интеллектуальные головоломки Шерлок Холмс с доктором Ватсоном, и описывает увлекательные приключения живых шахматных фигур в мире заколдованных замков, джинов и прочих чудес. Такие книги не просто интересно читать, они увлекают, возбуждают желание проверить свои возможности в ситуациях, в которых нужно мыслить строго логически и в то же время творчески, нестандартно.
Примечание сканировщика: в книге исправлены многочисленные орфографические ошибки, а также (не такие многочисленные) опечатки на диаграммах и в тексте решения задач.
Еще один отзыв: vk.com
P.S. The Chess Mysteries of Sherlock Holmes и The Chess Mysteries of the Arabian Knights можно найти в сети.
P.P.S. Как лучше перевести такой фрагмент:
Haroun Al Rashid --- The White king
Amelia --- His queen
?
Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.

скорее жив, чем.
Сборник тригонометрических уравнений с решениями от WA:
webmath.exponenta.ru/ege_15/p15.html
Ну и т.д.
воскресенье, 28 июня 2015
Здравствуйте! Нужно найти область сходимости степенного ряда:
`sum_(n = 1)^infty (a^n/n + b^n/n^2)*x^n`
На другом форуме мне подсказали: Пускай c=max(|a|,|b|). Рассмотрите случаи c<1, c=1, c>1.
Но я все равно не понимаю, как это применить. Может, кто-нибудь расшифрует?
Забыла указать (a > 0, b > 0)
`sum_(n = 1)^infty (a^n/n + b^n/n^2)*x^n`
На другом форуме мне подсказали: Пускай c=max(|a|,|b|). Рассмотрите случаи c<1, c=1, c>1.
Но я все равно не понимаю, как это применить. Может, кто-нибудь расшифрует?
Забыла указать (a > 0, b > 0)
Простыми словами
На мой взгляд, математику, в той степени, в которой он математик, нет нужды заниматься философией — более того, этого мнения придерживаются и многие философы. Анри Лебег. Scientific American 211 (September 1964) |
Сегодня, 28 июня, день рождения у выдающегося французского математика Анри Леона Лебега. В этом году ему исполнилось 140 лет.

Анри Леон Лебег (фр. Henri Léon Lebesgue; 28 июня 1875, Бове, департамент Уаза — 26 июля 1941, Париж) — французский математик, член Парижской АН (1922), член-корреспондент АН СССР (1929). Профессор Парижского университета (с 1910).
Биография
читать дальше
Достижения в математике
Первые исследования Лебега касались рядов Фурье. Позже он заинтересовался теорией интегрирования. Лебег считается одним из основателей современной теории функций действительной переменной. Создал теорию меры, внедрил понятие измеримой функции, ввел новое определение интеграла (интеграл Лебега), благодаря чему стало возможным интегрирование чрезвычайного широкого класса функций. Исследовал возможность аналитического изображения функций. Написал работы по теории размерности; доказал существование функций всех классов классификации Бэра; получил важные результаты геометрического и топологического характера; занимался исследованиями по вопросам теории функций, множеств и теории дифференцирования. В теории функций и в функциональном анализе широко известны такие понятия, как мера Лебега, интеграл Лебега, интеграл Лебега-Стилтьеса, лебеговские множества.
Интеграл Лебега
Интеграл Лебега — это обобщение интеграла Римана на более широкий класс функций.
Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла равны. Однако существует большой класс функций, определённых на отрезке и интегрируемых по Лебегу, но неинтегрируемых по Риману. Также интеграл Лебега может иметь смысл для функций, заданных на произвольных множествах (интеграл Фреше).
Идея построения интеграла Лебега состоит в том, что вместо разбиения области определения подынтегральной функции на части и составления потом интегральной суммы из значений функции на этих частях, на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.
А вот еще в качестве бонуса картинка из некоей Энциклобогии:
Задача Лебега
Задача Лебега состоит в отыскании плоской фигуры наименьшей площади, которая способна накрыть собой любую плоскую фигуру диаметра 1.
Замечание
Любая фигура диаметра 1 может быть накрыта фигурой постоянной ширины 1 (каждая фигура диаметра 1 — своей фигурой постоянной ширины, то есть фигура постоянной ширины зависит от фигуры диаметра 1). Для фигур постоянной ширины, диаметр совпадает с шириной. Поэтому задача Лебега сводится к нахождению плоской фигуры наименьшей площади, которая способна накрыть собой фигуру постоянной ширины 1.
Замечание в замечании
Кривая постоянной ширины `a` — плоская выпуклая кривая, длина ортогональной проекции которой на любую прямую равна a.
Иными словами, кривой постоянной ширины называется плоская выпуклая кривая, расстояние между любыми двумя параллельными опорными прямыми которой постоянно и равно `a` — «ширине» кривой.
Кривая постоянной ширины `a` — плоская выпуклая кривая, длина ортогональной проекции которой на любую прямую равна a.
Иными словами, кривой постоянной ширины называется плоская выпуклая кривая, расстояние между любыми двумя параллельными опорными прямыми которой постоянно и равно `a` — «ширине» кривой.
Примеры
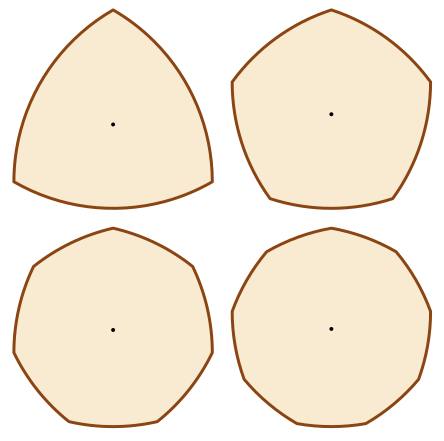
Треугольник Рёло - кривая постоянной ширины. Стороны квадрата - опорные прямые: каждая сторона касается треугольника, но не пересекает его. Треугольник Рёло можно вращать, и при этом он всегда будет касаться каждой стороны квадрата; таким образом ширина треугольника (расстояние между двумя опорными прямыми) постоянна.
Известно, что фигура Лебега существует, но она, возможно, не единственна. Если `L` её площадь, то известно, что
`0,826 < L < 0,845`.
Ссылки
1. Снова интересная статья на сайте, который я уже неоднократно рекомендовала math4school.ru.
2. Лебег А.Л. Об измерении величин. [Djv-ZIP] Перевод под редакцией А.Н.Колмогорова. (Москва: Учпедгиз, 1938). Книга
3. Тумаков И.М. Анри Леон Лебег. 1875-1941 [Djvu] М.: Наука, 1975. — 120 с. Книга
Необходимо найти оценку нормы матричной экспоненты `e^(tA)`, где `A = ((1,2,0),(-1,-1,0),(1,0,-1))`.
читать дальше
читать дальше
Проверьте еще эти задания, пожалуйста. Завтра пересдача и, надеюсь, что они будут последними. Голова болит уже от этих вероятностей)
Еще был бы вам очень признателен, если бы мне еще немного помогли в моих предыдущих темах:
1 тема
2 тема
Задания, часть I:
Решения, часть I:
Задания, часть II:
Решения, часть II:
Еще был бы вам очень признателен, если бы мне еще немного помогли в моих предыдущих темах:
1 тема
2 тема
Задания, часть I:
Решения, часть I:
Задания, часть II:
Решения, часть II:
суббота, 27 июня 2015
Торопись жить.
Задача.
При медицинском обследовании вероятность обнаружить заболевание «Т» у больного этим заболеванием равна 0,9. Вероятность принять здорового за больного равна 0,01. Доля больных с заболеванием «Т» по отношению ко всему населению равна 0,001. Найдите вероятность того, что человек здоров, если он был признан больным «Т» при обследовании.
Мое решение.
Пусть A - вероятность, что человек здоров
B - вероятность того, что человека признают больным.
P(A|B) - ?
P(A|B) = P(A)*P(B|A)/P(B)
P(A) = 0,999
P(B) = 0,9*0,001 + 0,999*0,01
P(B|A) = 0,01
Подставляем
P(A|B) = 0,999*0,01/0,01089 = 0,9
То есть получается, что вероятность того, что человек здоров, но его признали больным порядка 90%. Такого же быть не может. Подскажите, пожалуйста, в чем ошибка.
При медицинском обследовании вероятность обнаружить заболевание «Т» у больного этим заболеванием равна 0,9. Вероятность принять здорового за больного равна 0,01. Доля больных с заболеванием «Т» по отношению ко всему населению равна 0,001. Найдите вероятность того, что человек здоров, если он был признан больным «Т» при обследовании.
Мое решение.
Пусть A - вероятность, что человек здоров
B - вероятность того, что человека признают больным.
P(A|B) - ?
P(A|B) = P(A)*P(B|A)/P(B)
P(A) = 0,999
P(B) = 0,9*0,001 + 0,999*0,01
P(B|A) = 0,01
Подставляем
P(A|B) = 0,999*0,01/0,01089 = 0,9
То есть получается, что вероятность того, что человек здоров, но его признали больным порядка 90%. Такого же быть не может. Подскажите, пожалуйста, в чем ошибка.