[Amicus Plato]

Сумма двух долгов есть долг Брахмагупта

В этом году исполняется 1416 лет с рождения индийского математика и астронома Брахмагупты. А насколько он был выдающимся, можно судить уже лишь по тому, что спустя столько лет мы знаем и помним о нем.
Википедия
Брахмагупта, Брамагупта (санскр. ब्रह्मगुप्त, ок. 598—670) — индийский математик и астроном. Руководил обсерваторией в Удджайне. Оказал существенное влияние на развитие астрономии в Византии и странах ислама, стал использовать алгебраические методы для астрономических вычислений, ввёл правила операций с нулём, положительными и отрицательными величинами. До нашего времени сохранилось его основное сочинение «Брахма-спхута-сиддханта» («Усовершенствованное учение Брахмы», или «Пересмотр системы Брахмы»). Большая часть сочинения посвящена астрономии, две главы (12-я и 18-я) математике.

Биография
Брахмагупта родился приблизительно в 598 году. Это следует из книги «Брахма-спхута-сиддханта», в которой он сообщает, что написал этот текст в возрасте 30 лет в 628 году (Śaka 550). Брахмагупта родился в Бхилламале (современный Бхинмал в штате Раджастхан Северо-Западной Индии), который в то время был столицей земель династии Gurjara. Его отцом был Джиснугупта. Вероятно, он прожил большую часть жизни в Бхинмале во время правления (и, возможно, под покровительством) правителя Вьяграмукхи, поэтому его нередко именуют Бхилламакарья (учитель из Бхиллама). Брахмагупта был руководителем астрономической обсерватории в Удджайне. Обсерватория, в которой также работал Варахамихира, была лучшей в древней Индии.

На исследования Брахмагупты оказали серьёзное влияние его религиозные взгляды. Будучи правоверным индуистом, он критиковал космогологические воззрения некоторых его современников, в частности точку зрения Ариабхаты, утверждающего что Земля есть вращающаяся сфера. Брахмагупта спорил с Ариабхатой и о природе солнечных затмений:

Среди людей есть такие, которые думают, что затмения вызываются не Головой [дракона Раху]. Это абсурдное мнение, ибо это она вызывает затмения, и большинство жителей мира говорят, что именно она вызывает их. В Ведах, которые есть Слово Божие, из уст Брахмы говорится, что Голова вызывает затмения. Напротив того, Ариабхата, идя наперекор всем, из вражды к упомянутым священным словам утверждает, что затмение вызывается не Головой, а только Луной и тенью Земли… Эти авторы должны подчиниться большинству, ибо всё, что есть в Ведах — священно.

Голова Раху, желая отомстить Солнцу и Луне, иногда проглатывает их,
вызывая таким образом солнечные и лунные затмения

Хотя Брахмагупта был знаком с работами Ариабхаты, неизвестно, был ли он знаком также с работами Бхаскары. Работы Брахмагупты содержат многочисленные критические замечания в адрес современных ему астрономов, а содержание «Брахма-спхута-сиддханты» свидетельствует о расколе среди индийских математиков того времени. Разногласия были обусловлены в значительной степени выбором астрономических параметров и теории. Критика теорий оппонентов Брахмагупты содержится в первых двенадцати главах «Брахма-спхута-сиддханты» и отсутствует в тринадцатой и восемнадцатой главах.

Арабский учёный Аль-Бируни в своей книге «Китаб аль-Хинд» (около 1035) проанализировал и описал идеи индийских астрономов. В своей работе он ссылается на Брахмагупту как самый крупный авторитет.

Основные труды
Известно два основных труда Брахмагупты: Brahmasphutasiddhanta (Брахма-спхута-сиддханта), Khandakhadyaka (Кхандакхадьяка).
(Почитайте! Над этими текстами легко можно медитировать. Замечательное чтение )
Брахма-спхута-сиддханта
«Брахма-спхута-сиддханта» («Усовершенствованное учение Брахмы», или «Пересмотр системы Брахмы») — самый известный труд Брахмагупты, посвящённый математике и астрономии. Трактат написан стихами и содержит только результаты без доказательств. Труд состоит из 25 глав (в других источниках говорится о 24 главах и приложении с таблицами).

Первые 10 глав, которые представляют собой типичный текст по астрономии того периода, часто рассматриваются отдельно как первая версия работы, так как существуют манускрипты, содержащие только эти главы. Этот текст носит название Daśādhyāyī. В нём содержатся в частности расчёты средней и истинной долготы, вычисление суточного вращения, расчёт солнечных и лунных затмений, методы расчета положения небесных тел с течением времени (эфемериды), их восходов и заходов, соединений.

Следующие 15 глав содержат значительные дополнения и уточнения к первым главам, а также главы по математике. Математические главы дают представление о двух основных подходах индийских математиков: «математика процедур», или алгоритмы, и «математика семян», или уравнения. 12-я глава книги носит название «Математика», она посвящена простейшим арифметическим опериациям, пропорциям, задачам на смешение и рядам, что составляло основную часть практической математики во времена Брахмагупты. 18-я глава, «Распылитель», имеет прямое отношение к алгебре, но поскольку такого термина ещё не существовало, названа по первой задаче, рассматриваемой в главе.

Во второй половине VIII века, когда багдадский халиф из династии Аббасидов Абу-ль-Аббас Абд-Аллах аль-Мамун (712—775) был с посольством в Индии, пригласил в Багдад учёного из Удджайна по имени Канках, который преподавал индийскую систему астрономии на основе «Брахма-спхута-сиддханта». Халиф заказал письменный перевод книги на арабский язык, который был осуществлён математиком и философом Ибрахимом аль-Фазари в 771 году. Перевод, выполненный в виде таблиц — зиджа — с необходимыми пояснениями и рекомендациями, получил название «Большой Синдхинд». Известно, что этой работой пользовался ал-Хорезми для написания своих трудов по астрономии («Зидж ал-Хорезми») и арифметике («Книга об индийском счёте»). Считается, что перевод последней в XI веке на латинский язык сыграл решающую роль в распространении позиционной системы счисления.

"Брахма-спхута-сиддханта" была переведена китайскими математиками VII—IX веков (известно по крайней мере четыре перевода), позволив таким образом распространить десятичную систему среди китайских учёных. В 1817 году две математические главы были переведены на английский Генри Томасом Колбруком.

В 860 году индийский математик Prthudakasvami написал комментарии к работе, которые носят название Vāsanābhāṣya. От полных комментариев сохранилось только несколько манускриптов. Известно также несколько анонимных комментариев к полной версии сочинения и к первым десяти главам. В Индии работа Брахмагупты была опубликована в 1902 и 1966 годах.

Кхандакхадьяка
Вторая работа Брахмагупты, Кхандакхадьяка (A Piece Eatable), была написана в 665 году. Она состоит из 8 глав. В этой работе Брахмагупта уточнил и упростил ряд астрономических расчётов, пользуясь во многом системой, предложенной Ариабхатой. Кроме того, она включает интерполяционную формулу для вычисления синусов. В VIII веке Кхандакхадьяка была переведена на арабский язык под названием «Арканд».

Комментарии к Кхандакхадьяке были написаны в 864, 966, 1040, 1180 годы, некоторые из них не сохранились. Сама книга была напечатана в Калькутте в 1925 и 1941 году. Перевод на английский язык осуществил Сенгупта (Prabodh Chandra Sengupta) в 1934 году.

Вклад в математику
В своей работе Брахма-спхута-сиддханта Брахмагупта дал определение нуля как результат вычитания из числа самого числа. Он одним из первых установил правила арифметических операций над положительными и отрицательными числами и нулём, рассматривая при этом положительные числа как имущество, а отрицательные числа как долг. Далее Брахмагупта пытался расширить арифметику, дав определение деления на ноль. Согласно Брахмагупте,

• Деление нуля на нуль есть нуль;
• Деление положительного или отрицательного числа на нуль есть дробь с нулём в знаменателе;
• Деление нуля на положительное или отрицательное число есть нуль.

Брахмагупта предложил три метода умножения многозначных чисел в столбик (основной и два упрощённых), которые близки к тем, что используются в настоящее время. Основной метод Брахмапутра назвал «gomutrika», что в переводе Ифра означает «как траектория мочи коровы» (англ. "like the trajectory of cow's urine"; ).

Брахмагупта также предложил метод приближённого вычисления квадратного корня, эквивалентный итерационной формуле Ньютона (Newton-Raphson), метод решения некоторых неопределённых квадратных уравнений вида ax²+c=y², метод решения неопределённых линейных уравнений вида ax+c=by, используя метод последовательных дробей.

Он определил сумму квадратов и кубов первых n чисел через сумму первых n чисел, утверждая что «Сумма квадратов есть сумма чисел умноженная на удвоенное число шагов, увеличенное на единицу, и делённая на три. Сумма кубов есть квадрат суммы чисел до одного и того же числа».

В работе Кхандакхадьяка Брахмагупта предложил интерполяционную формулу второго порядка, являющуюся частным случаем выведенной более чем через 1000 лет интерполяционной формулы Ньютона — Стирлинга. Он использовал её для интерполяции значений синуса в составленных им тригонометрических таблицах. Формула даёт оценку значения функции f при значении её аргумента a + xh (при h > 0 и −1 ≤ x ≤ 1), когда её значение уже известно в точках a − h, a и a + h.

Формула Брахмагупты
Брахмагупта предложил формулу вычисления площади четырёхугольника, вписанного в окружность[3]. Формула Брахмагупты является обобщением формулы Герона для площади треугольника. А именно, площадь S вписанного в окружность четырёхугольника со сторонами a, b, c, d и полупериметром p равна
`S=sqrt((p-a)(p-b)(p-c)(p-d))`

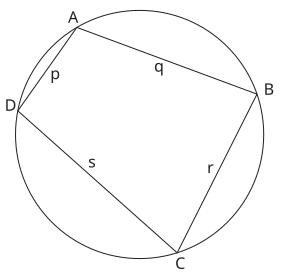
Формула Брахмагупты для четырёхугольника

(Стороны четырехугольника на картинке обозначены не так, но не будем придираться))
При этом сам Брахмагупта не уточнил, что формула верна только для четырёхугольников, которые можно вписать в окружность, поэтому некоторые историки полагают здесь ошибку Брахмагупты.

Известна ещё одна формула Брахмагупты для радиуса описанной окружности произвольного треугольника:

`R={ab}/{2h_c}={bc}/{2h_a}={ac}/{2h_b}`,
где `a`, `b`, `c` — стороны треугольника, `h_a`, `h_b` и `h_c` — его высоты.

Тождество Брахмагупты
Тождество Брахмагупты утверждает, что произведение двух сумм двух квадратов само является суммой двух квадратов, причём двояким образом.
`(a^2 + b^2)(c^2 + d^2) = (ac-bd)^2 + (ad+bc)^2 = (ac+bd)^2 + (ad-bc)^2`.
К примеру,
`(1^2 + 4^2)(2^2 + 7^2) = 26^2 + 15^2 = 30^2 + 1^2.`

Теорема Брахмагупты
Пусть имеется вписанный четырёхугольник, диагонали которого взаимно перпендикулярны. Опустим из точки пересечения диагоналей перпендикуляр на одну из его сторон. Будучи продолженным по другую сторону от точки пересечения диагоналей, этот перпендикуляр делит противоположную сторону четырёхугольника на две равные части.

Теорема Брахмагупты утверждает, что `AF = FD`

Задача Брахмагупты
Задача Брахмагупты — построить с помощью циркуля и линейки вписанный четырёхугольник по четырём его сторонам. Одно из решений использует окружность Аполлония.

Воспользуюсь своим положением и еще приведу картинку с окружностями Аполлония ))

Окружности Аполлония. Каждая голубая окружность пересекает каждую красную под прямым углом. Каждая красная окружность проходит через две точки (C и D) и каждая голубая окружность окружает только одну из этих точек
Википедия

@темы: История математики, Люди

Comments

[All_ex]

Amicus Plato, Спасибо!...

..

«как траектория мочи коровы» - какие у них всё-таки образные названия...

[Amicus Plato]

All_ex,

..

какие у них всё-таки образные названия...

Я вчера долго думала, выделить этот кусок или не выделять))) Решила не выделять, чтобы это было призом самому приметливому))) И за этим дело не стало))
Корова же — священное животное.
Вот, не далее как сегодня прочла у Олди:

Яджа принял из рук Панчалийца чашу бычьей мочи, плеснул бурую жидкость, крутанувшись винтом, - струя обернулась вокруг алтаря посолонь, слева направо, от следующего движения ятудхана святая моча описала "мертвецкое коло".

Amicus Plato, "Махабхарату" намного лучше и ярче пересказал еще Немировский.

[Amicus Plato]

Le levrier noir, спасибо

[All_ex]

Amicus Plato,

..

Корова же — священное животное. - от этого образность ничуть не страдает...