Простыми словами
Вчера, 14 марта, помимо дня Пи и дня рождения Альберта Эйнштейна, был еще день рожденья Вацлава Серпинского!
В прошлом году про него уже был топик с картинками.
Поэтому, чтобы не повторяться, вставлю небольшой, но интригующий отрывок из книги М. Шредера "Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая". Я эту книгу очень люблю и наверное рекламирую больше, чем необходимо, но меня извиняет то, что люблю и рекламирую я не только ее )
Игра сэра Пинского и детерминированный хаос
Рассмотрим следующую «настольную игру», в которой могут участвовать два и более человека.
Выигрывает тот, кто сумеет повторить удвоение расстояния от ближайшей вершину наибольшее число раз, не выходя при этом за пределы треугольника. Как мы увидим, существует несчетно много и в то же время очень мало точек, гарантирующих выигрыш или ничью. («Очень мало» надлежит понимать в том смысле, что случайно выбранная точка имеет нулевую вероятность сколь угодно продолжительного «выживания» игрока при соблюдении правил игры).
О том, что это за точки, можно узнать, прочитав книгу
И еще картинка про фракталы (математические печеньки). Ковер Серпинского там тоже присутствует )

В прошлом году про него уже был топик с картинками.
 | Серпинский (Серпиньский), Вацлав Франциск (польск. Wacław Franciszek Sierpiński; 14 марта 1882 — 21 октября 1969) |
Поэтому, чтобы не повторяться, вставлю небольшой, но интригующий отрывок из книги М. Шредера "Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая". Я эту книгу очень люблю и наверное рекламирую больше, чем необходимо, но меня извиняет то, что люблю и рекламирую я не только ее )
Игра сэра Пинского и детерминированный хаос
Рассмотрим следующую «настольную игру», в которой могут участвовать два и более человека.
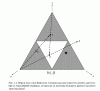
- Каждый игрок выбирает по своему усмотрению начальную точку внутри равностороннего треугольника.
- Проведя через ближайшую вершину и выбранную точку прямую и отложив на ней от этой вершины удвоенное расстояние до начальной точки, игрок получает точку `p_1`.
Выигрывает тот, кто сумеет повторить удвоение расстояния от ближайшей вершину наибольшее число раз, не выходя при этом за пределы треугольника. Как мы увидим, существует несчетно много и в то же время очень мало точек, гарантирующих выигрыш или ничью. («Очень мало» надлежит понимать в том смысле, что случайно выбранная точка имеет нулевую вероятность сколь угодно продолжительного «выживания» игрока при соблюдении правил игры).

О том, что это за точки, можно узнать, прочитав книгу

 | Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. - Ижевск: НИЦ «Регулярная и хаотическая динамика». 2001. - 528 с. Основная цель книги — помочь читателю глубже понять, что такое самоподобие — возможно, наиболее важную из встречающихся в природе симметрии, а также продемонстрировать широчайший диапазон применений масштабной инвариантности в физике, химии, биологии,музыке и, в особенности, в изобразительном искусстве. Материал изложен на доступном уровне и снабжен множеством иллюстраций. Книга будет полезна и интересна самому широкому кругу читателей. Скачать (djvu (rar), 3,1 mb) socifiles.com || ifolder |
И еще картинка про фракталы (математические печеньки). Ковер Серпинского там тоже присутствует )



-
-
16.03.2014 в 09:14Печеньки божественны...