Условие: читать дальше
Уже часа 4 над ним думаю,да вот ничего дельного не выходит.Скорее всего тут нужна подстановка Эйлера типа:t=sqrt(u^2+a^2)+u,но к сожалению,не могу понять как использовать её в данном примере.Заранее спасибо.Извиняюсь,что так поздно.
* a=const.
Уже часа 4 над ним думаю,да вот ничего дельного не выходит.Скорее всего тут нужна подстановка Эйлера типа:t=sqrt(u^2+a^2)+u,но к сожалению,не могу понять как использовать её в данном примере.Заранее спасибо.Извиняюсь,что так поздно.
* a=const.
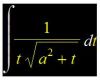
-
-
22.02.2010 в 02:20Пробовал?
-
-
22.02.2010 в 02:30Int(dx/x^2-a^2)=(1/2a)*ln|(x+a)/(x-a)|+C
-
-
22.02.2010 в 02:37А если самостоятельно и уникально, это всего лишь разложение в сумму двух дробей, ничего хитрого.
-
-
22.02.2010 в 02:41-
-
22.02.2010 в 02:45Ты просто разложи в сумму двух простейших дробей
1/(x^2-a^2)=1/2a(x-a)-1/2a(x+a)
-
-
22.02.2010 в 02:46-
-
22.02.2010 в 02:48-
-
22.02.2010 в 02:49у тебя тут числитель со знаменатель в логарифме перепутаны
Или я уж глюч,
Тротил, я пошла, уже не могу совсем.
-
-
22.02.2010 в 02:51-
-
22.02.2010 в 02:52Это типовая тема при изучении интегралов. Она позволяет брать интегралы от любых рациональных дробей (в теории
-
-
22.02.2010 в 02:56-
-
22.02.2010 в 08:08energy.bmstu.ru/gormath/mathan2s/undint/UnDefIn...
energy.bmstu.ru/gormath/mathan2s/undint/UnDefIn...
energy.bmstu.ru/gormath/mathan2s/undint/UnDefIn...
Будешь знать приемы - решишь в т.ч. и незнакомый для себя интеграл.
Особую сложность представляют собой радикалы - вот с ними лучше потренироваться дополнительно. А еще можно открыть Демимовича и посмотреть, какие интегралы к какой теме относятся. Сложные интегралы оттуда можно прорешать, легкие необязательно.
-
-
22.02.2010 в 11:38Но всё же тоже от уровня сложности зависит)
-
-
22.02.2010 в 12:38Как-то он их охарактеризовал..
не найдешь теперь..