Задача из контрольной для ВУЗа. Не срочно, но вам ведь не придется сильно много считать, поэтому расчитываю на оперативность. Пожалуйста.
Найти единичный вектор перпендикулярный векторам а=2i-j+k и b=-3i+4j+k и образующий с осью OZ тупой угол.
Решение. Найдем вектор перепендикулярный векторам а и b. Это есть их векторное произведение.
с=a*b
читать дальше
Так вот собственно вопрос: если я правильно понимаю +(-i-j+k) / √ 75 или -(-i-j+k) / √ 75 зависит от угла с осью OZ. Так вот если он тупой то какой знак получается ?
Найти единичный вектор перпендикулярный векторам а=2i-j+k и b=-3i+4j+k и образующий с осью OZ тупой угол.
Решение. Найдем вектор перепендикулярный векторам а и b. Это есть их векторное произведение.
с=a*b
читать дальше
Так вот собственно вопрос: если я правильно понимаю +(-i-j+k) / √ 75 или -(-i-j+k) / √ 75 зависит от угла с осью OZ. Так вот если он тупой то какой знак получается ?
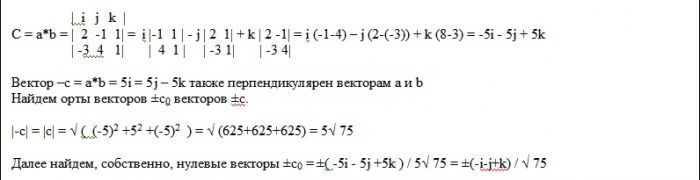
-
-
25.10.2009 в 16:05вот и посмотрите, какой из векторов образует с этим вектором тупой угол (по косинусу через скалярное произведение, например)
можно это сделать еще до ортов - отобрать нужный и лишь потом искать орт
-
-
25.10.2009 в 16:06У вас 5^2 почему 625?
-
-
25.10.2009 в 16:07А я даже и не заметила))
-
-
25.10.2009 в 16:16Ща буду исправлять...
-
-
25.10.2009 в 16:25Вот что-то мне подсказывает что координаты нужного вектора : 5(i+j-k) / √ 75
так как координата по оси z здесь отрицательна. Прально?
-
-
25.10.2009 в 16:34Через скалярное произведение найдите угол и всё.
-
-
25.10.2009 в 16:47Так чтоль ?
-
-
25.10.2009 в 16:48-
-
25.10.2009 в 16:56-
-
25.10.2009 в 17:36-
-
25.10.2009 в 17:48cos φ = (c*z) / |c|*|z|
|z| = √(0^2 + 0^2 + 1^2) = 1
cos φ1 = ( (-5)*0 + (-5)*0 + 5*1 ) / √ 75 * 1 = 5/ 5√5 = 1/√5 = 0.44721
cos φ2 = ( 5*0 + 5*0 - 5*1 ) / √ 75 * 1 = -5/ 5√5 = -1/√5 = -0,44721
величина cos φ1 =0,44721 соответствует углу ≈ 63 градуса - то есть он острый. Стало быть это не то что нам нужно.
Все-таки получается наш вектор - это вектор с (5, 5, -5)
Все правильно?
-
-
25.10.2009 в 18:03-
-
25.10.2009 в 18:14Так ?
-
-
25.10.2009 в 18:19-
-
25.10.2009 в 18:28А что, нельзя попроще объяснить что дескать так как нас интересует вектор составляющий тупой угол с осью OZ, то есть координата "k" которого отрицательна то решением является вектор с = (i/√5 + j/√5 - k/√5)
-
-
25.10.2009 в 18:31Это надо доказать. Здесь же всё сразу очевидно.
не думаю, что сложно потратить пол минуты на подсчёт косинуса
-
-
25.10.2009 в 18:33а откуда мы знаем, что это будет именно с отрицательной координатой
Если у вас там было что-то про направляющие косинусы и связь с координатами, то да. В противном случае лучше делать, как делали
-
-
25.10.2009 в 18:36cos φ2 = ( 5*0 + 5*0 - 5*1 ) / √ 75 * 1 = -5/ 5√5 = -1/√5 = -0,44721 - какому углу соответствует это значение ? В таблице брадиса отрицательных значений нет.... Я представляю какую глупость сейчас спрашиваю но все же....
-
-
25.10.2009 в 18:41в первой четверти (острый угол) косинус положительный
А во второй четверти (от90 до 180) косинус отрицательный
Школа - 9 , наверное, класс
Именно по знаку косинуса определяется тупой или острый угол
-
-
25.10.2009 в 18:43ищите в таблице брадиса для 0,44 и вычитайте этот угол из 180
-
-
25.10.2009 в 18:45На окружности посмотрите и убедитесь, что угол тупой. Сам угол никто не спрашивает
-
-
25.10.2009 в 18:49Но вообще-то я так и считал. Спасибо вам всем ОГРОМНОЕ за помощь.
Но обращаюсь к вам не последний раз - в этой работе еще одна задача плюс еще одна контрольная по производным....
Там вообще мрак...