извините,что снова обращаюсь к вам с мольбой о помощи. но сессия на носу, а с вышкой мне не совладать. если сможете, объясните что как ,зачем и почему, дабы понять все то о чем будут говорить на экзамене.
срок до пятницы. первый курс, заочное отделение. еще раз спасибо!
найти предел, пользуясь правилом Лопиталя.

исследовать функцию построить график.

найти неопределенный интеграл. результат проверить дифференцированием.

найти неопределенный интеграл используя формулу интегрирования по частям.

вычислить определенные интегралы используя подстановки,указанные в скобках

вычислить не собственный интеграл или доказать его расходимость

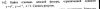

найти наибоьшее и наименьшее значение ф-и z(x,y) в указанной замкнутой области D/сделать рисунок.

найти в точке А полный дифференциал ф-и y(x) заданной неявно.

срок до пятницы. первый курс, заочное отделение. еще раз спасибо!
найти предел, пользуясь правилом Лопиталя.

исследовать функцию построить график.

найти неопределенный интеграл. результат проверить дифференцированием.

найти неопределенный интеграл используя формулу интегрирования по частям.

вычислить определенные интегралы используя подстановки,указанные в скобках

вычислить не собственный интеграл или доказать его расходимость

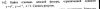

найти наибоьшее и наименьшее значение ф-и z(x,y) в указанной замкнутой области D/сделать рисунок.

найти в точке А полный дифференциал ф-и y(x) заданной неявно.











-
-
25.05.2009 в 22:41-
-
25.05.2009 в 23:22совладать. если сможете, объясните что как ,зачем и почему, дабы понять все то о чем будут говорить на экзамене.
Здесь объем теории страниц 100-150 нужен, чтобы понимать все задания и решения к ним.
-
-
25.05.2009 в 23:26-
-
25.05.2009 в 23:35Это и есть "издали" )))
Ну, минимум - страниц 70. Это если вы хорошо схватываете математические тексты.
Дело в том, что почти к каждому заданию совершенно новая теория страниц 5-15. А так 1 тема в учебнике реально занимает 20-50 страниц. Вот и считайте.
-
-
25.05.2009 в 23:38Так что надо было сначала все потихоньку учить а не оставлять на последний день.
-
-
25.05.2009 в 23:41Больше, чем семестр
Я сам слушал математику в Бауманке
-
-
25.05.2009 в 23:44-
-
26.05.2009 в 00:36Соболь Практикум по высшей математике
Рябушко часть 1, 2
Там определения, основные теоремы и образцы решения типовых задач.
Руководства по решению задач ("Решебники" по высшей математике)