УЧП

[Люцианна]

Уравнения в частных производных (они же уравнения матфизики - вот только физики там пока ни на грош).
Проблема следующая в обоих номерах:

2.3: пункты 6 и 7; 2.11: пункты 5 и 8.
Моя не понимать, как решать уравнения где присутствует сама функция u - там, где ее различные производные все решается понятными стандартными методами замены, а вот с самой функцией что делать?
И еще: когда после замены пересчитывают вторые производные, а в первых при этом присутствуют переменные x и y, я не понимаю, как находить вторые производные (которые получаются как сложные производные с этими самыми переменными) - буду безмерно благодарна, если кто-нибудь сможет мне объяснить, желательно на примере.
Сдавать - завтра.

@темы: Дифференциальные уравнения

Comments

[Robot]

Может быть вот это поможет?
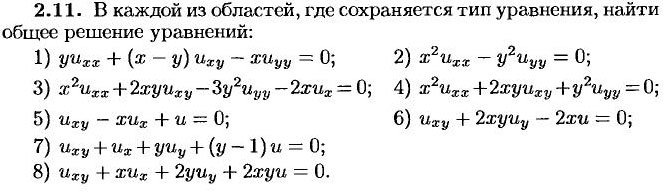
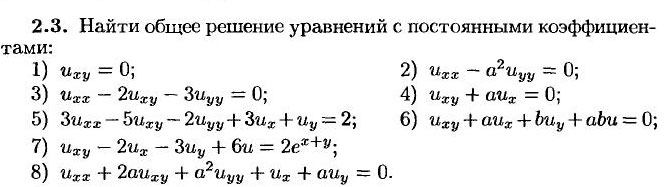
Решебник. Высшая математика. Специальные разделы/ Под ред.Кириллова. - М.: Физматлит, 2003. -400с.
Книга содержит примеры решения типовых задач по теории функций комплексной переменной, операционному исчислению, рядам Фурье, преобразованию Фурье, уравнениям математической физики, теории вероятностей и математической статистике. Каждой задаче отведен отдельный раздел, содержащий общую постановку задачи, план ее решения с необходимыми теоретическими пояснениями и решение конкретного примера. Кроме того, в раздел включены десять задач для cамостоятельного решения и ответы к ним.
Размер: 2.22 Мб
Ссылка для скачивания файла: ifolder.ru/6785774

[Люцианна]

Robot, спасибо большое. Насчет u я поняла. А вот как производную вычислять - там нет, там сразу вычисленные(

[Robot]

К сожалению, я вообще со всем этим дела не имела.
Пыталась разобраться, но там ведь сначала первого порядка, а потом уже это. Не осилила(((

[Люцианна]

Robot, да с первым порядком там все предельно просто... Со вторым, если в первом порядке не остается x и у - тоже все просто. А вот со вторым с переменными...

[mpl]

Владелец дневника видит IP-адреса пользователей, оставивших комментарии!