подскажите пож с решением вот этих примеров

[princeton_girl]

не могу разобраться вот с задачкой )нужно найти площадь по формуле ньютона лейбница..помогите разобратьс или я график не правильно построила или что ?((
1)
(дано указание)

2. вот ещё пример вроде делаю по шагам всё думаю правильно но в самом конце не могу проинтегрировать тангенс

(дано указание)

3, 4. и вот ещё два примера с ними я зашла в полный ступор (да перечитала столько литературы видно мозг у меня не воспринимает точные науки (совсем не могу тут решить ...в первом где по частям не могу интеграл найти от косинус в квадрате
а во втором примере думаю нужно подвести под диференциал но как там ведь корень ....вообщем помогите плз(((

Даны указания

@темы: Приложения определенного интеграла, Интегралы, Дифференциальные уравнения

Comments

[Trotil]

Там где 1/tg(x). На самом деле решается заменой y=sin(x).

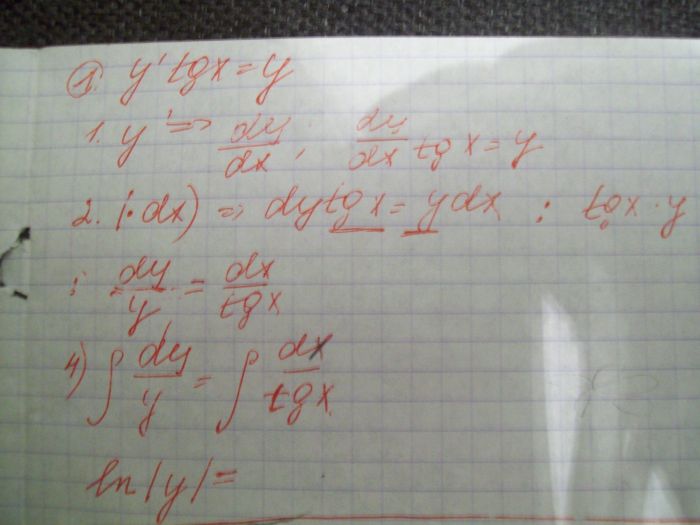
cos^2(x) - здесь нужно понижать степень.

> думаю нужно подвести под диференциал но как там ведь корень

Корень совсем не помеха. Будет типа dy/sqrt(y) = 2 * sqrt(y)

[Robot]

princeton_girl
Еще раз напоминаю, что рисунки надо скрывать под тегом more. В этот раз я сама это сделала, в с ледующий раз - сообщение будет игнорироваться , пока не будет приведено к правилам.
Не указаны сроки.
Задания надо выкладывать не в комментах, а в посте, поскольку поиск ведется среди записей, но не среди комментов.
Учтите это на будущее.
В задании с площадью фигуры неправильно построен график параболы
Далее если сверху график функции y=f1(x), а снизу y=f2(x), то площадь равна ∫(f1(x)-f2(x))dx с расставленными пределами

[Солнечная Клюква]

самый последний интеграл - табличный.
интеграл xdx/sqrt(a^2-x^2)= - sqrt(a^2-x^2)

[Robot]

Солнечная Клюква
Ну, он не совсем табличный. В таблицах низшего уровня его нет.
Но, действительно, если ввести замену a^2-x^2=y, то -2xdx=dy
xdx=-(1/2)dy
∫xdx/sqrt(a^2-x^2)=-(1/2)∫dy/sqrt(y)=-(1/2)∫y^(-1/2)dy=-y^(1/2)+C=- sqrt(a^2-x^2)+C
(Это я не для тебя пишу, а для princeton_girl )
Можно и внесением под знак дифференциала

[Robot]

princeton_girl
В зад. 3 Неправильно обозваны u и dv

Например, можно так
u=x
dv=dx/cos^2(x)

[Гость]

sqrt А что вот это обозначает?

[Солнечная Клюква]

Гость sqrt(y) - это корень из у