.sex on the beach.
1. Задачи с параметрами.
2. 10 класс, с/р
3. а) Найдите все значения a , при каждом из которых любое действительное число х является решением неравенства
х^2 + (2а + 1)х - а/4>0

б) Найдите все значения а, при каждом из которых уравнение х^2 + (а + 1)х + 9 = 0 имеет два различных корня, больших 2
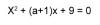
4. Буду очень благодарна за помощь, срок до вечера воскресенья. Вроде не оч сложное, но я торможу.
2. 10 класс, с/р
3. а) Найдите все значения a , при каждом из которых любое действительное число х является решением неравенства
х^2 + (2а + 1)х - а/4>0

б) Найдите все значения а, при каждом из которых уравнение х^2 + (а + 1)х + 9 = 0 имеет два различных корня, больших 2
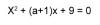
4. Буду очень благодарна за помощь, срок до вечера воскресенья. Вроде не оч сложное, но я торможу.


-
-
24.11.2007 в 16:05К примеру второе:
Чтобы было два корня нужно чтобы дискриминант был больше нуля.
Д = a^2 + 2a -35
Отсюда корни будут:
x1 = [-a - 1 - SQRT (a^2 + 2a -35)]/2
x2 = [-a - 1 + SQRT (a^2 + 2a -35)]/2
Ну и будет у вас система из трех уравнений
a^2 + 2a -35> 0
[-a - 1 - SQRT (a^2 + 2a -35)]/2 > 2
[-a - 1 + SQRT (a^2 + 2a -35)]/2 > 2
Отсюда а найти плевое дело.
-
-
24.11.2007 в 16:05Неравенство заведомо квадратное (внимание: если бы перед x^2 стоял параметр обязательно отдельно надо было бы рассматривать случай, когда он равен 0)
Коэффициент при x^2 положителен, следовательно, парабола, являющаяся графиком кв. трехчлена, направлена ветвями вверх.
Отсюда неравенство верно при любом действительном х , когда этот график ось ОХ не пересекает ("висит" над осью ОХ), а это будет, если дискриминант меньше 0
D=(2a+1)^2+4*(a/4)<0
(2a+1)^2+a<0
Остается решить это неравенство
-
-
24.11.2007 в 16:07Да уж, плевое )))
-
-
24.11.2007 в 16:11Я уже давала ссылки, но вот еще раз
pay.diary.ru/~eek/?comments&postid=37874967#156...
-
-
24.11.2007 в 16:16Рассмотрим уравнение x^2+px+q=0 (1`)
Здесь в условии задачи не сказано, что два различных корня, поэтому условие D=>0
У нас же имеет два различных корня, больших 2, поэтому D>0
-
-
24.11.2007 в 16:16-
-
24.11.2007 в 16:20Ок, спасибо большое.
А вот насчет второго, есть пример решия подобной задачи.
"Пример 1: Найдем все значения а, при каждом из которых ур-е х^2 + ax +9 = 0 имеет два различныз корня, меньших -1.
Решение: Т.к. ур-е должно иметь два различных корня, то должно выполняться нер-во D=a^2>0 //это понятно//. Так как коэф. при x^2 больше нуля, то для того, чтобы оба корня были меньше -1, должны выполняться два условия: абцисса Хо = - а/2 вершины параболы - графика f(x) = x^2 + ax + 9 должна быть меньше -1 //это тоже понятно// и значение ф-и в точке -1 должно быть положительным //туплю, но вот это не понятно//
Дальше решается системой))
-
-
24.11.2007 в 16:26Это решение как раз того типа, что приведено у меня выше
Посмотри - это все видно из графика.
Т.к. ур-е должно иметь два различных корня, то должно выполняться нер-во D=a^2 + 2a -35>0
Раз оба корня больше 2, то и абсцисса вершины параболы тоже больше двух
И посмотри на чертеже - видишь, значение функции в точке 2 положительно? Если ты будешь рассматривать другое расположение (когда, например, один корень больше 2 , а другой меньше, то значение функции в точке 2 будет отрицательным
-
-
24.11.2007 в 16:29Решать вот такие неравенства - это довольно громоздко
[-a - 1 - SQRT (a^2 + 2a -35)]/2 > 2
[-a - 1 + SQRT (a^2 + 2a -35)]/2 > 2
Не поняла насчет выражения из первого и подстановки во второе
.deleted
Я советую скачать вот это
www.rgrta.ryazan.ru/abitur/Mathdocs/menu31.htm
Там это разбирается поподробнее
А вот здесь есть примеры
www.rgrta.ryazan.ru/abitur/Mathdocs/zadach.htm
-
-
24.11.2007 в 16:34Кстати, спасибо, что оформила просьбу по всем правилам!
-
-
24.11.2007 в 16:38-
-
24.11.2007 в 16:40Пожалуйста.
Значит у меня получается f(2) = 2a +17>0 так?
И система тогда:
a^2 + 2a -35 > 0
- (a + 1)/2 > 2
2a +17>0
-
-
24.11.2007 в 16:57Кроме сокращения оч. я не вижу орфографических, грамматических и прочих ошибок))))
.deleted
Не обращай на него внимания))) Он такой... А дневник у него!...
У меня f(2)=2a+15
-
-
24.11.2007 в 17:002. 10 класс, с/р [нет точки вконце предложения.]
3. а) Найдите все значения a , при каждом из которых любое действительное число х является решением неравенства
х^2 + (2а + 1)х - а/4>0 [после "а" стоит лишнай пробел, оборот "при каждом из которых" несовсем правильно построен, после скобки (2а + 1) не стоит знак умножения, нет точки вконце предложения.]
б) Найдите все значения а, при каждом из которых уравнение х^2 + (а + 1)х + 9 = 0 имеет два различных корня, больших 2 [нет точки вконце предложения, нет знака умножить, оборот описанный выше.]
4. Буду очень благодарна за помощь, срок до вечера воскресенья. Вроде не оч сложное, но я торможу. [после сокращения "оч" не стоит точка]
Придраться можно к чему угодно, было бы желание
-
-
24.11.2007 в 17:07Точно, там f(2)=2a+15. Повторюсь, спасибо большое. И спасибо за ссылки, полезная вещь.
Паломник Оптимизма
О, ну подумаешь, не так много ошибок. Тем более "оборот "при каждом из которых" несовсем правильно построен" это не моя вина, а того, кто составлял задачу.
-
-
24.11.2007 в 17:08Прямо не знаю, что с тобой делать
Иди, дифуры решай))
-
-
24.11.2007 в 17:10Пожалуйста)
-
-
24.11.2007 в 17:18.deleted не обижайся, я это не в упрек тебе написал, а милая пикировка с роботом )
-
-
26.11.2007 в 04:50Это точно, например, можно придираться к придирающимся, ну, вот, скажем
a^2 + 2a -35> 0
зачем уж обязательно раскрывать удобненькую скобку: (а+1)^2>36 )))
Да и "несовсем" пишется раздельно ))) А еще "вконце" - точно раздельно пишется, ну и:
оборот описанный выше
Во-во, оборот - причастный оборот отделяется запятой от предшествующего определяемого слова )))
и т п. Придираться - это иногда бывает забавно )))
-
-
26.11.2007 в 08:34-
-
26.11.2007 в 13:23и у меня. А еще у меня по алгебре три и по геометрии три, и те с натяжкой (без шуток), и еще пять троек в аттестате )))))
-
-
26.11.2007 в 13:27-
-
01.03.2013 в 14:15