Step by step ... Informazioni sulle gare, come allenarsi, chi corrompere.
Этап проводился дистанционно. На ввод ответов отводилось 120 минут.
9 класс
читать дальше1. Найдите наибольшее пятизначное число, произведение цифр которого равно 120.
2. В течение первого полугодия лентяй Паша заставлял себя решать задачи по математике. Каждый день он решал не более 10 задач, а если в какой-нибудь день он решал больше 7 задач, то следующие два дня он решал не более 5 задач в день. Какое наибольшее количество задач Паша мог решить за 7 подряд идущих дней?
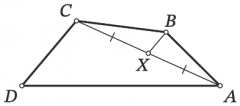
3. Дан выпуклый четырёхугольник $ABCD,$ $X$ --- середина диагонали $AC.$ Оказалось, что $CD\parallel BX.$ Найдите $AD,$ если известно, что $BX=3,$ $BC=7,$ $CD=6.$

4. Про положительные числа $a, b, c$ известно, что \[ \frac {a+b+c}{a+b-c} = 7,\quad \frac {a+b+c}{a+c-b} = 1{,}75. \]
Чему равняется $\dfrac {a+b+c}{b+c-a}?$
5. Точка $M$ --- середина стороны $BC$ треугольника $ABC,$ в котором $AB=17,$ $AC=30,$ $BC=19.$ На стороне $AB$ как на диаметре построена окружность. На этой окружности выбирается произвольная точка $X.$ Какое минимальное значение может принимать длина отрезка $MX?$


6. Дана белая клетчатая таблица $8\times8.$ В ней 20 клеток покрасили в чёрный цвет. Какое наименьшее количество пар соседних по стороне белых клеток могло остаться?
7. Стороны квадрата $ABCD$ параллельны осям координат, причём $AB$ лежит на оси ординат, а сам квадрат расположен так, как показано на рисунке. Парабола, задаваемая уравнением \[ y = \frac {1}{5}x^2 + ax + b,\] проходит через точки $B$ и $C.$ Кроме этого, вершина этой параболы (точка $E$) лежит на отрезке $AD.$ Найдите сумму корней квадратного трёхчлена, графиком которого является парабола.


8. По кругу стоят 73 ребёнка. Злой Дед Мороз обходит круг по часовой стрелке и раздаёт конфеты. Вначале он выдал первому ребёнку одну конфету, затем 1 ребёнка пропустил, следующему ребёнку выдал одну конфету, затем 2 детей пропустил, следующему ребёнку выдал одну конфету, затем 3 детей пропустил и так далее. Раздав 2020 конфет, он ушёл. Сколько детей так и не получили конфеты?
10 класс
читать дальше1. На какое наименьшее число клетчатых прямоугольников можно разрезать фигуру на рисунке? (Каждый прямоугольник должен состоять из одной или нескольких клеток фигуры.)


2. Сколько корней имеет уравнение \[ \overbrace{f(f(...f}^{10\text{ раз }f}(x)...)) + \frac {1}{2} = 0, \] где $f(x) = |x|-1?$
3. Антон выписал на доску три натуральных числа: $a,$ $b$ и $c.$ А Ира нарисовала на доске три прямоугольника: $a\times b,$ $a\times c$ и $b\times c.$ Оказалось, что разность площадей какой-то пары прямоугольников равна $1,$ а разность площадей другой пары прямоугольников равна 49. Чему может быть равно $a+b+c?$ Укажите все возможные варианты.
4. Равнобедренная трапеция $ABCD$ с основаниями $BC$ и $AD$ такова, что $\angle ADC = 2\angle CAD = 82^\circ.$ Внутри трапеции выбрана точка $T$ так, что $CT=CD,$ $AT=TD.$ Найдите $\angle TCD.$


5. Целые числа $a$ и $b$ таковы, что у квадратных трёхчленов $x^2+ax+b$ и $x^2+bx+1100$ есть общий корень, являющийся простым числом. Найдите $a.$ Укажите все возможные варианты.
6. На острове живут два племени: рыцари и лжецы. Рыцари всегда говорят правду, а лжецы всегда лгут. Однажды 80 человек сели за круглый стол, и каждый из них заявил: «Среди 11 человек, сидящих следом за мной по часовой стрелке, есть хотя бы 9 лжецов». Сколько рыцарей сидит за круглым столом? Укажите все возможные варианты.
7. Дан прямоугольный треугольник $ABC$ с катетами $AB=42$ и $BC=56.$ Окружность, проходящая через точку $B,$ пересекает сторону $AB$ в точке $P,$ сторону $BC$ --- в точке $Q,$ а сторону $AC$ --- в точках $K$ и $L.$ Известно, что $PK=KQ$ и $QL:PL=3:4.$ Найдите $PQ^2.$


8. Два разбойника украли 300 золотых монет. Они решили поделить их следующим образом: первый разбойник кладёт в мешочек несколько монет (возможно, все), а второй разбойник выбирает, кому этот мешочек достанется; затем это действие повторяется ещё несколько раз. Делёж заканчивается, когда
либо все деньги кончились,
либо кому-нибудь досталось 11 мешочков, в этом случае все остальные деньги сразу же достаются другому разбойнику.
Какое наибольшее количество монет может гарантированно получить первый разбойник?
11 класс
читать дальше1. Учитель написал на доске двузначное число. Каждый из троих ребят сказал по два утверждения.
Андрей: «это число заканчивается на цифру 6» и «это число делится на 7».
Боря: «это число больше 26» и «это число заканчивается на цифру 8».
Саша: «это число делится на 13» и «это число меньше 27».
Известно, что каждый из мальчиков один раз сказал правду и один раз ошибся. Какое число могло быть написано на доске? Укажите все возможные варианты.
2. У Веры есть набор различных по массе гирь, каждая из которых весит целое число грамм. Известно, что самая лёгкая гиря набора весит в 71 раз меньше, чем все остальные гири вместе взятые. Также известно, что две самые лёгкие гири набора вместе весят в 34 раза меньше, чем все остальные гири вместе взятые. Какое наименьшее число грамм может весить самая лёгкая гиря?
3. На координатной плоскости отметили все точки $(x, y)$ такие, что $x$ и $y$ --- целые числа, удовлетворяющие неравенствам $0\le x\le 2$ и $0\le y\le 26.$ Сколько существует прямых, проходящих ровно через 3 отмеченные точки?
4. На стороне $AC$ треугольника $ABC$ отмечены точки $M$ и $N$ ($M$ лежит на отрезке $AN$). Известно, что $AB=AN,$ $BC=MC.$ Описанные окружности треугольников $ABM$ и $CBN$ пересекаются в точках $B$ и $K.$ Сколько градусов составляет угол $AKC,$ если $\angle ABC = 68^\circ?$


5. В шахматном турнире соревнуются друг с другом команда школьников и команда студентов, в каждой из которых по 15 человек. В течение турнира каждый школьник должен сыграть с каждым студентом ровно один раз, причём каждый день каждый человек должен играть не более одного раза. В некоторый момент турнира организатор заметил, что может составить расписание на следующий день из 15 игр ровно 1 способом, а из 1 игры --- $N$ способами (порядок игр в расписании не важен, важно лишь кто с кем играет). Найдите наибольшее возможное значение $N.$
6. Дан выпуклый четырёхугольник $ABCD.$ Известно, что $\angle C 57^\circ,$ $\sin \angle A + \sin \angle B = \sqrt{2}$ и $\cos \angle A + \cos \angle B = 2 - sqrt{2}.$ Сколько градусов составляет угол $D?$
7. Натуральные числа $a$ и $b$ таковы, что $a^a$ делится на $b^b,$ однако $a$ не делится на $b.$ Найдите наименьшее возможное значение числа $a+b,$ если известно, что число взаимно просто с 210.
8. Внутри тетраэдра $ABCD$ даны точки $X$ и $Y.$ Расстояния от точки $X$ до граней $ABC,$ $ABD,$ $ACD,$ $BCD$ равны 14, 11, 29, 8 соответственно. А расстояния от $Y$ точки до граней $ABC,$ $ABD,$ $ACD,$ $BCD$ равны 15, 13, 25, 11 соответственно. Найдите радиус вписанной сферы тетраэдра $ABCD.$


vos.olimpiada.ru/main/table/tasks/#table
9 класс
читать дальше1. Найдите наибольшее пятизначное число, произведение цифр которого равно 120.
2. В течение первого полугодия лентяй Паша заставлял себя решать задачи по математике. Каждый день он решал не более 10 задач, а если в какой-нибудь день он решал больше 7 задач, то следующие два дня он решал не более 5 задач в день. Какое наибольшее количество задач Паша мог решить за 7 подряд идущих дней?
3. Дан выпуклый четырёхугольник $ABCD,$ $X$ --- середина диагонали $AC.$ Оказалось, что $CD\parallel BX.$ Найдите $AD,$ если известно, что $BX=3,$ $BC=7,$ $CD=6.$


4. Про положительные числа $a, b, c$ известно, что \[ \frac {a+b+c}{a+b-c} = 7,\quad \frac {a+b+c}{a+c-b} = 1{,}75. \]
Чему равняется $\dfrac {a+b+c}{b+c-a}?$
5. Точка $M$ --- середина стороны $BC$ треугольника $ABC,$ в котором $AB=17,$ $AC=30,$ $BC=19.$ На стороне $AB$ как на диаметре построена окружность. На этой окружности выбирается произвольная точка $X.$ Какое минимальное значение может принимать длина отрезка $MX?$


6. Дана белая клетчатая таблица $8\times8.$ В ней 20 клеток покрасили в чёрный цвет. Какое наименьшее количество пар соседних по стороне белых клеток могло остаться?
7. Стороны квадрата $ABCD$ параллельны осям координат, причём $AB$ лежит на оси ординат, а сам квадрат расположен так, как показано на рисунке. Парабола, задаваемая уравнением \[ y = \frac {1}{5}x^2 + ax + b,\] проходит через точки $B$ и $C.$ Кроме этого, вершина этой параболы (точка $E$) лежит на отрезке $AD.$ Найдите сумму корней квадратного трёхчлена, графиком которого является парабола.


8. По кругу стоят 73 ребёнка. Злой Дед Мороз обходит круг по часовой стрелке и раздаёт конфеты. Вначале он выдал первому ребёнку одну конфету, затем 1 ребёнка пропустил, следующему ребёнку выдал одну конфету, затем 2 детей пропустил, следующему ребёнку выдал одну конфету, затем 3 детей пропустил и так далее. Раздав 2020 конфет, он ушёл. Сколько детей так и не получили конфеты?
10 класс
читать дальше1. На какое наименьшее число клетчатых прямоугольников можно разрезать фигуру на рисунке? (Каждый прямоугольник должен состоять из одной или нескольких клеток фигуры.)


2. Сколько корней имеет уравнение \[ \overbrace{f(f(...f}^{10\text{ раз }f}(x)...)) + \frac {1}{2} = 0, \] где $f(x) = |x|-1?$
3. Антон выписал на доску три натуральных числа: $a,$ $b$ и $c.$ А Ира нарисовала на доске три прямоугольника: $a\times b,$ $a\times c$ и $b\times c.$ Оказалось, что разность площадей какой-то пары прямоугольников равна $1,$ а разность площадей другой пары прямоугольников равна 49. Чему может быть равно $a+b+c?$ Укажите все возможные варианты.
4. Равнобедренная трапеция $ABCD$ с основаниями $BC$ и $AD$ такова, что $\angle ADC = 2\angle CAD = 82^\circ.$ Внутри трапеции выбрана точка $T$ так, что $CT=CD,$ $AT=TD.$ Найдите $\angle TCD.$


5. Целые числа $a$ и $b$ таковы, что у квадратных трёхчленов $x^2+ax+b$ и $x^2+bx+1100$ есть общий корень, являющийся простым числом. Найдите $a.$ Укажите все возможные варианты.
6. На острове живут два племени: рыцари и лжецы. Рыцари всегда говорят правду, а лжецы всегда лгут. Однажды 80 человек сели за круглый стол, и каждый из них заявил: «Среди 11 человек, сидящих следом за мной по часовой стрелке, есть хотя бы 9 лжецов». Сколько рыцарей сидит за круглым столом? Укажите все возможные варианты.
7. Дан прямоугольный треугольник $ABC$ с катетами $AB=42$ и $BC=56.$ Окружность, проходящая через точку $B,$ пересекает сторону $AB$ в точке $P,$ сторону $BC$ --- в точке $Q,$ а сторону $AC$ --- в точках $K$ и $L.$ Известно, что $PK=KQ$ и $QL:PL=3:4.$ Найдите $PQ^2.$


8. Два разбойника украли 300 золотых монет. Они решили поделить их следующим образом: первый разбойник кладёт в мешочек несколько монет (возможно, все), а второй разбойник выбирает, кому этот мешочек достанется; затем это действие повторяется ещё несколько раз. Делёж заканчивается, когда
либо все деньги кончились,
либо кому-нибудь досталось 11 мешочков, в этом случае все остальные деньги сразу же достаются другому разбойнику.
Какое наибольшее количество монет может гарантированно получить первый разбойник?
11 класс
читать дальше1. Учитель написал на доске двузначное число. Каждый из троих ребят сказал по два утверждения.
Андрей: «это число заканчивается на цифру 6» и «это число делится на 7».
Боря: «это число больше 26» и «это число заканчивается на цифру 8».
Саша: «это число делится на 13» и «это число меньше 27».
Известно, что каждый из мальчиков один раз сказал правду и один раз ошибся. Какое число могло быть написано на доске? Укажите все возможные варианты.
2. У Веры есть набор различных по массе гирь, каждая из которых весит целое число грамм. Известно, что самая лёгкая гиря набора весит в 71 раз меньше, чем все остальные гири вместе взятые. Также известно, что две самые лёгкие гири набора вместе весят в 34 раза меньше, чем все остальные гири вместе взятые. Какое наименьшее число грамм может весить самая лёгкая гиря?
3. На координатной плоскости отметили все точки $(x, y)$ такие, что $x$ и $y$ --- целые числа, удовлетворяющие неравенствам $0\le x\le 2$ и $0\le y\le 26.$ Сколько существует прямых, проходящих ровно через 3 отмеченные точки?
4. На стороне $AC$ треугольника $ABC$ отмечены точки $M$ и $N$ ($M$ лежит на отрезке $AN$). Известно, что $AB=AN,$ $BC=MC.$ Описанные окружности треугольников $ABM$ и $CBN$ пересекаются в точках $B$ и $K.$ Сколько градусов составляет угол $AKC,$ если $\angle ABC = 68^\circ?$


5. В шахматном турнире соревнуются друг с другом команда школьников и команда студентов, в каждой из которых по 15 человек. В течение турнира каждый школьник должен сыграть с каждым студентом ровно один раз, причём каждый день каждый человек должен играть не более одного раза. В некоторый момент турнира организатор заметил, что может составить расписание на следующий день из 15 игр ровно 1 способом, а из 1 игры --- $N$ способами (порядок игр в расписании не важен, важно лишь кто с кем играет). Найдите наибольшее возможное значение $N.$
6. Дан выпуклый четырёхугольник $ABCD.$ Известно, что $\angle C 57^\circ,$ $\sin \angle A + \sin \angle B = \sqrt{2}$ и $\cos \angle A + \cos \angle B = 2 - sqrt{2}.$ Сколько градусов составляет угол $D?$
7. Натуральные числа $a$ и $b$ таковы, что $a^a$ делится на $b^b,$ однако $a$ не делится на $b.$ Найдите наименьшее возможное значение числа $a+b,$ если известно, что число взаимно просто с 210.
8. Внутри тетраэдра $ABCD$ даны точки $X$ и $Y.$ Расстояния от точки $X$ до граней $ABC,$ $ABD,$ $ACD,$ $BCD$ равны 14, 11, 29, 8 соответственно. А расстояния от $Y$ точки до граней $ABC,$ $ABD,$ $ACD,$ $BCD$ равны 15, 13, 25, 11 соответственно. Найдите радиус вписанной сферы тетраэдра $ABCD.$


vos.olimpiada.ru/main/table/tasks/#table
@темы: Олимпиадные задачи
-
-
14.12.2020 в 11:36