| |
Я утверждаю, что приведенные цитаты лишь доказывают тот факт, что ни один из тех математиков так и не удосужился тщательно рассмотреть аккуратно построенную кривую Пеано. Кто-нибудь менее добродушный мог бы сказать, что эти цитаты демонстрируют полное отсутствие геометрического воображения.
Бенуа Мандельброт. Фрактальная геометрия природы |
27 августа исполнилось
155 лет со дня рождения Джузеппе Пеано.

Википедия
Джузеппе Пеано (итал. Giuseppe Peano; 1858—1932) — итальянский математик. Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино-сине-флексионе. Более всего известен как автор стандартной аксиоматизации натуральной арифметики — арифметики Пеано.
(Вот и всё, что сказано о нем в Википедии).
Конечно, первое, о чем нужно написать, это арифметика Пеано.
Аксиомы Пеано Аксиомы Пеано в свое время сделали огромный прорыв в математике. Бертран Рассел писал, какое огромное впечатление произвела эта аксиоматика на него и на Уайтхеда.
Аксиомы Пеано — одна из систем аксиом для натуральных чисел.
Аксиомы Пеано позволили формализовать арифметику. После введения аксиом стали возможны доказательства многих свойств натуральных и целых чисел, а также использование целых чисел для построения формальных теорий рациональных и вещественных чисел.
О неполнотеКак следует из теоремы Гёделя о неполноте, существуют утверждения о натуральных числах, которые нельзя ни доказать, ни опровергнуть, исходя из аксиом Пеано. Некоторые такие утверждения имеют достаточно простую формулировку, например теорема Гудстейна.
Словесная формулировка- 1 является натуральным числом;
- Число, следующее за натуральным, тоже является натуральным;
- 1 не следует ни за каким натуральным числом;
- Если натуральное число `a` непосредственно следует как за числом `b`, так и за числом `c`, то `b` и `c` тождественны;
- (Аксиома индукции.) Если какое-либо предложение доказано для 1 (база индукции) и если из допущения, что оно верно для натурального числа `n`, вытекает, что оно верно для следующего за `n` натурального числа (индукционное предположение), то это предложение верно для всех натуральных чисел.
(Математическую формулировку я приводить, с вашего позволения, не буду)
Латино-сине-флексионечитать дальшеЛатино-сине-флексионе (Latino sine flexione — латынь без словоизменения) — международный искусственный язык на основе латинского языка, созданный итальянским математиком Джузеппе Пеано в 1903 году. После доработки в 1908 году стал называться интерлингва (не следует путать с другим искусственным языком с аналогичным названием — см. Интерлингва  ).
).
В Википедии дано очень развернутое описание этого языка.
Для всех желающих прошу!Кривая ПеаноВикипедияНа этой теме остановлюсь более подробно.
Кривая Пеано — общее название для параметрических кривых, образ которых содержит квадрат (или, в более общем смысле, открытые области пространства).
Звучит, может быть, устрашающе, и на самом деле, так и есть. )
Не буду останавливаться на аналитических свойствах кривых Пеано, хотя там масса всего интересного.
Для начала займемся геометрическим построением.
Геометрическое построение. Рассмотрим единичный отрезок и единичный квадрат. На 1-м шаге построения разделим квадрат средними линиями на 4 равных квадратика, а отрезок - на 4 равные части. Получим квадратики и отрезочки 1-го уровня. На каждом последующем шаге делим квадратики и отрезочки предыдущего уровня на 4 части - получаем квадратики и отрезочки следующего уровня. Имеем 4 квадратика 1-го уровня, 16 квадратиков 2-го уровня и т.д.; аналогично с отрезочками. Зададим порядок обхода квадратиков каждого уровня. Для 1-го, 2-го, ..., 6-го уровня порядок обхода показан на рисунке. Порядок обхода определяет взаимно-однозначное соответствие между множеством квадратиков n-го уровня и множеством отрезочков n-го уровня.
Пусть теперь x - произвольная точка исходного единичного отрезка. Пусть k1 - номер отрезочка 1-го уровня, которому принадлежит точка x, k2 - номер отрезочка 2-го уровня, которому принадлежит точка x и т.д. Рассмотрим квадратики Q1, Q2, ... с теми же номерами k1, k2, .... Порядок обхода квадратиков устроен таким образом, что (внимание!) квадратики Q1, Q2, ... образуют вложенную систему. По теореме о вложенной (стягивающейся) системе отрезков, квадратики Q1, Q2, ... имеют единственную общую точку y.
Если x принадлежит одновременно 2-м отрезочкам, то эти отрезочки соответствуют 2-м квадратикам с общей стороной - так устроен порядок обхода. Назовем такие квадратики смежными. В этом случае вместо квадратиков Q1, Q2, ... рассмотрим прямоугольники - объединения смежных квадратиков. И тогда y - единственная общая точка вложенной системы указанных прямоугольников.
Аналогичное рассуждение показывает, что каждая точка y квадрата будет соответствовать некоторой точке x единичного отрезка.
Построенное отображение x → y определяет искомую кривую Пеано. Непрерывность отображения следует из того, что близким отрезочкам соответствуют близкие квадратики. Каждая точка y имеет:
- 1 прообраз x (если y не принадлежит границам 2-х несмежных квадратиков никакого уровня),
- 2 прообраза (если y принадлежит границам не более 2-х несмежных квадратиков некоторого уровня),
- 3 прообраза (если y принадлежит границам 4-х квадратиков некоторого уровня, одна пара которых - смежные),
- 4 прообраза (если y принадлежит границам 4-х попарно несмежных квадратиков некоторого уровня).


Пример кривой Пеано, построенный Гильбертом. Здесь показан порядок обхода квадратиков 1-6 уровня.Математическая энциклопедия

Построение кривой Пеано для треугольника
Известный интерес представляют т. н. правильные замкнутые кривые типа Пеано - пределы последовательностей симметричных замкнутых кривых, соответствующих последовательностям триангуляции произвольного правильного многоугольника, каждая из К-рых является правильным (т. е. полученным делением на Две равные части) подразделением предыдущей (пример - на рис. 2). При этом последовательность кривых можно выбрать так, чтобы предел площадей областей, ими ограниченных, был равен заданной величине (даже нулю или площади всей подразделяемой фигуры) (рис. 3). Кажется вероятным, что подобные картинки могут быть полезны при исследовании роста кристаллич. структур. Аналогично с помощью последовательностей триангуляции можно строить отображения прямой в плоскость, в частности "периодические" кривые типа Пеано.
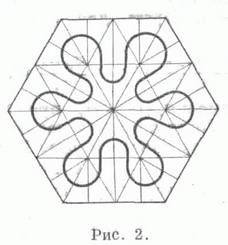

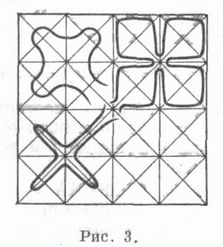

Эти картинки и их описание взяты из математической энциклопедииИ напоследок еще одна картинка
(с)



 ).
).




-
-
31.08.2013 в 22:56читать дальше
-
-
31.08.2013 в 23:05UPD читать дальше
-
-
31.08.2013 в 23:19-
-
31.08.2013 в 23:28-
-
31.08.2013 в 23:32-
-
01.09.2013 в 00:33-
-
01.09.2013 в 00:35читать дальше
-
-
01.09.2013 в 14:01-
-
01.09.2013 в 16:56