воскресенье, 09 июня 2013
| |
Я поступал совершенно иначе, что позволило мне все более и более расширять условия, которыми я себя ограничивал, пока я не заметил, что принципиальная трудность вопроса может быть, с помощью одного искусственного приема, обойдена в самом общем случае.
Таким образом, мне удалось получить очень общий результат, доказывающий справедливость теоремы при условиях, значительно более общих, чем дополненные Марковым условия теоремы Чебышева, причем он получен мною с помощью анализа, не зависящего от какой-либо специальной теории, и основан только на самых элементарных соображениях.
А.М. Ляпунов. Об одной теореме теории вероятностей
|
6 июня исполнилось
156 лет со дня рождения
Александра Михайловича Ляпунова.

Википедия
Александр Михайлович Ляпунов (25 мая (6 июня) 1857, Ярославль — 3 ноября 1918, Одесса) — русский математик и механик, академик Петербургской Академии наук с 1901 г., член-корреспондент Парижской академии наук, член Национальной академии деи Линчеи (Италия) и ряда других академий наук и научных обществ.
Биографиячитать дальшеВ Википедии довольно подробная статья о биографии Александра Михайловича — от детских лет и до трагической гибели...
Не буду ее сюда переписывать.
Лучше немного расскажу о его научных результатах.Научные результатыНу, в первую очередь, с именем Ляпунова (по крайней мере у меня) связана
устойчивость по Ляпунову. С нее и начну.
Устойчивостьчитать дальшеВ математике, решение дифференциального уравнения (или, шире, траектория динамической системы) называется устойчивым, если поведение решений с близким начальным условием «не сильно отличается» от поведения исходного решения. Слова «не сильно отличается» при этом можно формализовать по-разному, получая разные формальные определения устойчивости: устойчивость по Ляпунову, асимптотическую устойчивость и т.д. Обычно рассматривается задача об устойчивости тривиального решения в особой точке, поскольку задача об устойчивости произвольной траектории сводится к данной путем замены неизвестной функции.
Лучшая иллюстрация устойчивого и неустойчивого равновесия вот такая.
(Чтобы меня не привлекли за нарушение авторских прав, нарисую сама)
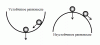
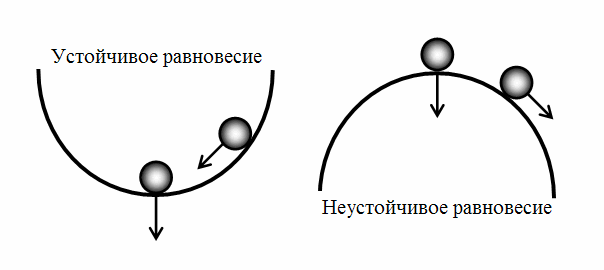
Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия при малых возмущениях. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.
Что касается формального определения устойчивости по Ляпунову — в нем ничего сложного нет, но я, пожалуй, ограничусь ссылкой на ту же Википедию. ВотВремя Ляпуновачитать дальшеВремя Ляпунова — время, за которое система приводится к полному хаосу. Оно определено как время, за которое расстояние между соседними траекториями системы возрастает в `e` раз. Время Ляпунова отражает пределы предсказуемости системы.Ну и та-дамм!
Фрактал Ляпуновачитать дальшеФракталы Ляпунова (также известные как фракталы Маркуса-Ляпунова) — бифуркационные фракталы, порождённые расширением логистического отображения, в которых степень роста совокупности `r` периодически меняет значение с `A` на `B` и наоборот.
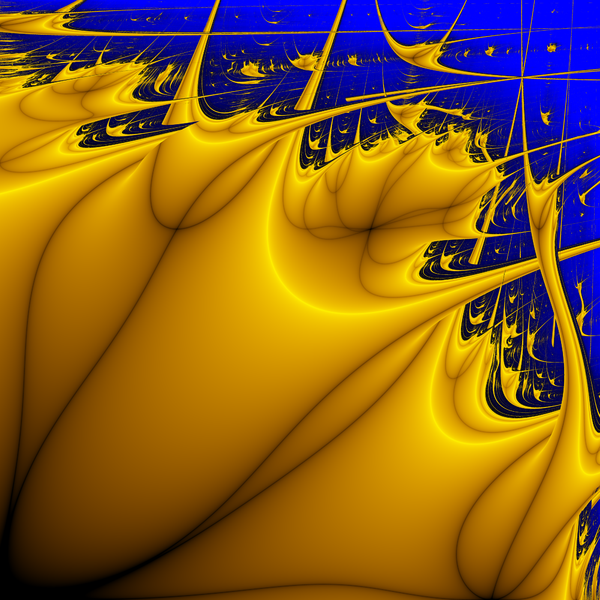
Фракталы Ляпунова строятся отображением областей стабильного и хаотического поведения, измеряемых экспонентой Ляпунова `\lambda`, в плоскости `a-b` для данной периодической последовательности `a` и `b`. На рисунках жёлтый цвет соответствует стабильности (`\lambda < 0`), а синий - хаосу (`\lambda > 0`).
Стандартный логистический фрактал Ляпунова с итерационной последовательностью AB в области [2, 4] x [2, 4]:


Обобщённый логистический фрактал Ляпунова с итерационной последовательностью BBBBBBAAAAAA; зона роста параметра -- в области [3.4, 4.0] x [2.5, 3.4]. Также известен как Zircon City:


Обобщённый логистический фрактал Ляпунова с итерационной последовательностью AABAB в области [2, 4] x [2, 4]:

Свойства
Фракталы Ляпунова обычно строятся для значений `A` и `B` в интервале `[0,4]`. Для бо́льших значений интервал `[0,1]` уже не стабилен, и последовательность вероятнее всего стремится к бесконечности, хотя для некоторых параметров всё ещё существуют сходящиеся циклы конечных значений. У всех итерационных последовательностей диагональ `a = b` такая же, как у стандартной логистической функции с одним параметром.
Последовательность обычно начинается со значения 0,5, которое является критической точкой итеративной функции. Другие (обычно комплекснозначные) критические точки итеративной функции одного полного цикла - это те, которые проходят через значение 0,5 в первом цикле. Сходящийся цикл должен содержать по меньшей мере одну критическую точку, поэтому все сходящиеся циклы могут быть получены всего лишь сдвигом итерационной последовательности с сохранением начального значения 0,5. На практике сдвиг этой последовательности приводит к изменениям фрактала, поскольку некоторые ветви перекрываются другими. Например, обратите внимание, что фрактал Ляпунова для итерационной последовательности `AB` не идеально симметричен относительно `a` и `b`.
Алгоритм генерации фракталов Ляпунова
- Выбрать строку из символов `A`, `B`, `C` и `D` любой нетривиальной длины (например, AABABCCAADDCD).
- Построить последовательность `S` последовательных символов строки, повторённых необходимое число раз.
- Выбрать точку `(a,b) \in [0,4] \times [0,4]`.
- Выбрать точку `(c,d) \in [4,0] \times [4,0]`.
- Определить функцию `r_n = {(a, S_n = A),( b, S_n = B), (c, S_n = C), (d, S_n = D):}`.
- Принять `x_0 = 0,5` и выполнить итерации `x_{n+1}=r_nx_n(1 - x_n)`.
- Вычислить экспоненту Ляпунова:
`\lambda = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{n = 1}^N \log | dx_{n + 1} /(dx_n) | = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{n = 1}^N \log |r_n(1 - 2x_n)|` - Раскрасить точку `(a,b) + (c,d)` согласно полученному значению `\lambda`.
- Повторить шаги 3-7 для каждой точки плоскости изображения.
На практике `\lambda` аппроксимируется подбором достаточно великого N. Этот алгоритм подходит для таких языков, как Mathematica, но не для языков низкого уровня.Ссылки на сайты с фракталами Ляпунова. (Очень красиво!))1.
EFG's Fractals and Chaos - Lyapunov Exponents2.
Elert, Glenn Lyapunov Space3.
Element90 Fractals Книги
 |
Александр Михайлович Ляпунов Шибанов А. С. Жизнь замечательных людей. Молодая гвардия. 1985
Книга посвящена жизни и деятельности выдающегося русского математика и механика, академика А.М. Ляпунова (1857-1918), разработавшего ряд научных направлений, не потерявших своей значимости и сегодня. Созданная им строгая и общая теория устойчивости признана во всем мире, а разработанные Ляпуновым методы лежат в основе большинства современных исследований устойчивости. Используя архивные материалы, автор воссоздает жизненный и творческий путь А. М. Ляпунова на фоне научной жизни России конца XIX - начала XX века, тесно переплетавшийся с судьбами его братьев - композитора С.М. Ляпунова и академика-слависта Б.М. Ляпунова.
Скачать (djvu, 32 Мб) libgen.org |
 |
Избранные труды Ляпунов Александр Михайлович, Редакция В.И.Смирнова. Комментарии С.Н.Бернштейна, Л.Н.Сретенского и Н.Г.Четаева. Издательство Академии Наук СССР. 1948.
Скачать (djvu, 6 Мб) libgen.org
ОГЛАВЛЕНИЕОГЛАВЛЕНИЕ: Общая задача об устойчивости движения (7). Предисловие (9). Глава I. Предварительный анализ (17). Постановка вопроса (17). О некоторых системах линейных дифференциальных уравнений (37). О некотором общем случае дифференциальных уравнений возмущенного движения (63). Некоторые общие предложения (79). О некоторых вопросах, связанных с задачей Дирихле (97). Предисловие (99). Глава I. Вспомогательные предложения и допущения (102). Глава II. Основная задача электростатики (131). Глава III. Задача Дирихле (146). Об одной теореме теории вероятностей (179). Новая форма теоремы о пределе вероятности (239). Исследования в теории фигуры небесных тел (251). О форме небесных тел (303). ПРИЛОЖЕНИЯ: Биография А.М.Ляпунова. Академик В.И.Смирнов (325). Очерк научных трудов А.М.Ляпунова. Академик В.И.Смирнов (341). I. Устойчивость равновесия и движения механических систем с конечным числом степеней свободы (344). II. Фигуры равновесия равномерно вращающейся жидкости (395). III. Работы по устойчивости фигур равновесия вращающейся жидкости (423). IV. Различные работы (444). Комментарий к главе I работы «Общая задача об устойчивости движения». Член-корреспондент АН СССР Н.Г.Четаев (451). Комментарий к работе «О некоторых вопросах, связанных с задачей Дирихле» Член-корреспондент АН СССР Л.Н.Сретейский (457). Комментарий к работам по теории вероятностей. Академик С.Н.Бернштейн (477). Комментарий к работе «Исследования в теории фигуры небесных тел». Член-корреспондент АН СССР Л.Н.Сретенский (484). Примечание к лекции А.М.Ляпунова. «О форме небесных тел». Академик А.Я.Крылов (493). Библиографический указатель печатных трудов и материалов о жизни и деятельности А.М.Ляпунова. А.М.Лукомская (495). I. Работы А.М.Ляпунова, опубликованные в печати (495). II. Материалы о жизни и деятельности А.М.Ляпунова (511). III. Основная научная литература, относящаяся к работам А.М.Ляпунова (521).
|
@темы:
История математики,
Люди







-
-
09.06.2013 в 20:02-
-
09.06.2013 в 21:40-
-
10.06.2013 в 01:06читать дальше
-
-
11.06.2013 в 11:38Она есть в сети libgen.net/view.php?id=140910
Меня всегда интересовала деревенька, откуда они все родом