С2

[yonkis]

В правильной шестиугольной пирамиде SABCDEF,‍ стороны основания ABCDEF‍ которой равны 1, а боковые рёбра равны 2, найдите угол между прямыми SF‍ и BM,‍ где M -середина ребра SC.‍

рисунок

Решение:
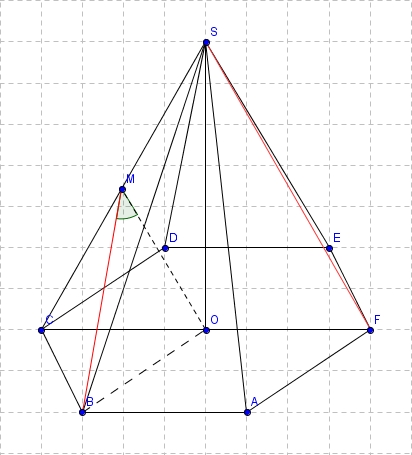
Проведем OM - средняя линия тр-ка CSF, OM||FS, тогда угол BMO - искомый

как решать дальше?

@темы: Стереометрия, ЕГЭ

Comments

[VEk]

как решать дальше?

Теорема косинусов Вам в помощь.

[yonkis]

OB=R впис окр
OM найдем из прямоуг тр-ка CMO
а как BM найти?

[VEk]

Формулу длины медианы знаете? `m_c=1/2*sqrt(2a^2+2b^2-c^2)`

[yonkis]

не изучали, но теперь буду знать
а как по-другому можно?

[VEk]

По-другому? Например, через векторы или координаты.
А формула эта является следствием теоремы: "Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон". Ее обычно дают в виде задачи на применение теорему косинусов.

[yonkis]

а может какие дополнительные построения? или никак не решить, не применив формулу?

[VEk]

Длину BM можно найти еще из треугольника BCM по теореме косинусов.

[yonkis]

а как тогда угол MCB найти?

[VEk]

Провести высоту боковой грани.