Всё должно быть сделано настолько простым, насколько это возможно, но не проще. А. Энштейн
Итоги студенческой олимпиады
Итак, наконец-то собравшись с силами и со временем, спешу поделиться с вами результатами олимпиады, проводившейся не так давно.
В целом, участники порадовали, не порадовало одно - многие из записавшихся не участвовали - так ни по одной задаче и не выложили. Но, это их право.
Представлю вам оргкомитет олимпиады:
VEK, Alidoro, Heor, _ТошА_
К вышеперечисленным можно обращаться по всем вопросам оценивая и проч. в комментариях записи.
Конечно нельзя забыть Robot, которая хоть формально и не числится в оргкомитете из-за лишней скромности, но очень-очень нам помогала, без неё ничего бы не вышло.
Ну и, собственно, результаты:
1 место - Alisa_Selezneva
2 место - vyv2
3 место - Mist*, nvse
Так же участвовал школьник, абсолютно верно решивший одну задачу: Rus-Kira
Поздравляем их с очень хорошим выступлением! У всех были очень интересные решения, спасибо!
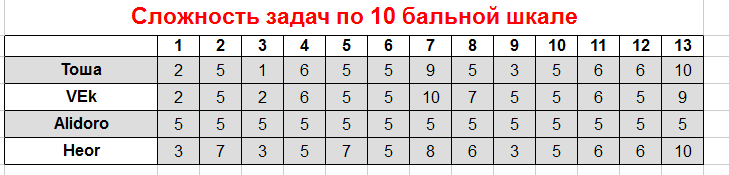
Теперь немного про оценивание. Сначала о таком параметре, как сложность задач.
Каждый проверяющий выставил свой балл каждой задаче - от 0 до 10 в порядке увеличения сложности (10 - очень сложная, 0 - элементарная).
Вот таблица, показывающая распределившиеся баллы сложности по задачам:
читать дальше
За задачу каждый участник получал от 0 до 1 балла. Затем бралась средняя оценка из выставленных. Не все проверяющие поставили баллы по всем задачам: причины различны. Таблицы выставленных оргкомитетом баллов:
Alisa_Selezneva
Mist*
vyv2
nvse
Собственно, баллы пересчитывались вот по какой формуле:
Расчёт коэффициента сложности k = (среднее арифметическое сложностей, выставленных оргкомитетом)*(количество участников)/(5*(количество решивших))
Количество баллов по i-ой задаче, выставленных участнику:
n = (среднее арифметическое из оценок, выставленных оргкомитетом)*`k_i`
И сама таблица баллов:
читать дальше
А теперь решения от составителей:
1) Решить в `ZZ`: `3x^2 - 7xy +2y^2 + 19x - 18y = -35`
Решение:
читать дальше
2) Найти сумму:
`cos(x) + C_n^1cos(2x) + ... + C_n^ncos((n+1)x)`
Решение:
читать дальше
3) Найти функцию `f(x)` `x in (0, 1)`, если `f'(sin^2(x)) = cos(2x) + tg^2(x)`
Решение:
читать дальше
4) Пусть `t` - дифференцируема на `[a, b]` функция, `t(a) = t(b) = 0`. Доказать, что существует `c in (a, b): t(c) = t '(c)`
Решение:
читать дальше
5) Пусть `f` - бесконечно дифференцируемая функция. Решить функциональное уравнение: `f(x+y) = f(x) + f(y) +xy(x^2/3 + xy/2 + y^2/3)`, зная что `f(2) = -2`
Решение:
читать дальше
6) Решить функциональное уравнение: `2xf(x) + f(1/(1-x)) = 2x`
Решение:
читать дальше
7) `x_1 in (0, 1)` `x_(n+1) = ln(1 + x_n)` Найти `lim_(n->oo) n*x_n`
Решение:
читать дальше
8) Вычислить: `lim_(n->oo) ((n+1)ln(n!) - 2ln(2!3!...n!))/(n^2)`
Решение:
читать дальше
9) Вычислить: `int_(-1)^1 (ln(1+x^2))/(1+e^x)dx`
Решение:
читать дальше
10) Найти общее решение диф. уравнения: `(x^2 + 1)((y')^2 - yy'')= xyy'`
Решение:
читать дальше
11) Найти общее решение диф. уравнения: `y' = y/(y^2 + 1)(1/x + ye^x - y^2/x)`
Решение:
читать дальше
12) Параметры `a` и `b` меняются так, что система
`{(y = ax + 1), (x^2 + y^2 = 2bx):}`
имеет единственное решение `(x_0, y_0)`. Какую кривую при этом описывает точка `M_0(x_0, y_0)`?
Решение:
читать дальше
13) Пусть `a_1 < a_2 < ... < a_k <= n`, - такой конечный набор натуральных чисел, наименьшее кратное любых двух из которых больше `n`. Доказать, что `sum_(i=1)^k 1/a_i < 2`
Решение:
читать дальше
Итак, наконец-то собравшись с силами и со временем, спешу поделиться с вами результатами олимпиады, проводившейся не так давно.
В целом, участники порадовали, не порадовало одно - многие из записавшихся не участвовали - так ни по одной задаче и не выложили. Но, это их право.
Представлю вам оргкомитет олимпиады:
VEK, Alidoro, Heor, _ТошА_
К вышеперечисленным можно обращаться по всем вопросам оценивая и проч. в комментариях записи.
Конечно нельзя забыть Robot, которая хоть формально и не числится в оргкомитете из-за лишней скромности, но очень-очень нам помогала, без неё ничего бы не вышло.
Ну и, собственно, результаты:
1 место - Alisa_Selezneva
2 место - vyv2
3 место - Mist*, nvse
Так же участвовал школьник, абсолютно верно решивший одну задачу: Rus-Kira
Поздравляем их с очень хорошим выступлением! У всех были очень интересные решения, спасибо!
Теперь немного про оценивание. Сначала о таком параметре, как сложность задач.
Каждый проверяющий выставил свой балл каждой задаче - от 0 до 10 в порядке увеличения сложности (10 - очень сложная, 0 - элементарная).
Вот таблица, показывающая распределившиеся баллы сложности по задачам:
читать дальше
За задачу каждый участник получал от 0 до 1 балла. Затем бралась средняя оценка из выставленных. Не все проверяющие поставили баллы по всем задачам: причины различны. Таблицы выставленных оргкомитетом баллов:
Alisa_Selezneva
Mist*
vyv2
nvse
Собственно, баллы пересчитывались вот по какой формуле:
Расчёт коэффициента сложности k = (среднее арифметическое сложностей, выставленных оргкомитетом)*(количество участников)/(5*(количество решивших))
Количество баллов по i-ой задаче, выставленных участнику:
n = (среднее арифметическое из оценок, выставленных оргкомитетом)*`k_i`
И сама таблица баллов:
читать дальше
А теперь решения от составителей:
1) Решить в `ZZ`: `3x^2 - 7xy +2y^2 + 19x - 18y = -35`
Решение:
читать дальше
2) Найти сумму:
`cos(x) + C_n^1cos(2x) + ... + C_n^ncos((n+1)x)`
Решение:
читать дальше
3) Найти функцию `f(x)` `x in (0, 1)`, если `f'(sin^2(x)) = cos(2x) + tg^2(x)`
Решение:
читать дальше
4) Пусть `t` - дифференцируема на `[a, b]` функция, `t(a) = t(b) = 0`. Доказать, что существует `c in (a, b): t(c) = t '(c)`
Решение:
читать дальше
5) Пусть `f` - бесконечно дифференцируемая функция. Решить функциональное уравнение: `f(x+y) = f(x) + f(y) +xy(x^2/3 + xy/2 + y^2/3)`, зная что `f(2) = -2`
Решение:
читать дальше
6) Решить функциональное уравнение: `2xf(x) + f(1/(1-x)) = 2x`
Решение:
читать дальше
7) `x_1 in (0, 1)` `x_(n+1) = ln(1 + x_n)` Найти `lim_(n->oo) n*x_n`
Решение:
читать дальше
8) Вычислить: `lim_(n->oo) ((n+1)ln(n!) - 2ln(2!3!...n!))/(n^2)`
Решение:
читать дальше
9) Вычислить: `int_(-1)^1 (ln(1+x^2))/(1+e^x)dx`
Решение:
читать дальше
10) Найти общее решение диф. уравнения: `(x^2 + 1)((y')^2 - yy'')= xyy'`
Решение:
читать дальше
11) Найти общее решение диф. уравнения: `y' = y/(y^2 + 1)(1/x + ye^x - y^2/x)`
Решение:
читать дальше
12) Параметры `a` и `b` меняются так, что система
`{(y = ax + 1), (x^2 + y^2 = 2bx):}`
имеет единственное решение `(x_0, y_0)`. Какую кривую при этом описывает точка `M_0(x_0, y_0)`?
Решение:
читать дальше
13) Пусть `a_1 < a_2 < ... < a_k <= n`, - такой конечный набор натуральных чисел, наименьшее кратное любых двух из которых больше `n`. Доказать, что `sum_(i=1)^k 1/a_i < 2`
Решение:
читать дальше





-
-
27.03.2011 в 13:40Действительно, решения были очень интересные.
Например, решение Alisa_Selezneva второй задачи (более простоe, чем официальное)
2) Найти сумму:
`cos(x) + C_n^1cos(2x) + ... + C_n^ncos((n+1)x)`.
Решение.
Пусть `S=cos(x) + C_n^1cos(2x) + ... + C_n^ncos((n+1)x)` искомая сумма.
Рассмотрим сумму
`S_1=C_n^0*(cos(x)+i*sin(x))+ C_n^1*(cos(2x)+i*sin(2x))+ ... +C_n^n*(cos((n+1)x)+i*sin((n+1)x))` и заметим, что `S=R e(S_1)`.
Преобразуем выражение для `S_1`, используя первую формулу Муавра, формулу бинома Ньютона и правило умножения комплексных чисел, записанных в тригонометрической форме.
`S_1=C_n^0*(cos(x)+i*sin(x)) + C_n^1*(cos(x)+i*sin(x))^2+… C_n^n*(cos(x)+i*sin(x))^ (n+1)=`[Замена: `z=cos(x)+i*sin(x)`]`= C_n^0*z + C_n^1*z^2+… C_n^n*z^(n+1)=z*( C_n^0 + C_n^1*z+… C_n^n*z^n)=z*(1+z)^n=(cos(x)+i*sin(x))*(1+cos(x)+i*sin(x))^n=(cos(x)+i*sin(x))*(2cos^2(x/2)+i*2sin(x/2)cos(x/2))^n=2^n*cos^n(x/2)*(cos(x)+i*sin(x))*(cos(x/2)+i*sin(x/2))^n=2^n*cos^n(x/2)*(cos(x)+i*sin(x))*(cos((nx)/2)+i*sin((nx)/2))= 2^n*cos^n(x/2)*(cos((n+2)/2*x)+i*sin((n+2)/2*x))= 2^n*cos^n(x/2)*cos((n+2)/2*x)+i*2^n*cos^n(x/2)* sin((n+2)/2*x).
Следовательно, `S=R e(S_1)= 2^n*cos^n(x/2)*cos((n+2)/2*x)`.
Ответ: `2^n*cos^n(x/2)*cos((n+2)/2*x)`.
-
-
27.03.2011 в 14:43-
-
27.03.2011 в 16:14Я считаю, что для нашего сообщества это очень хороший опыт, который будет способствовать выявлению и развитию математических способностей участников сообщества, раскрытию их творческого потенциала.
Лично для меня подготовка к самой олимпиаде оказалась очень продуктивной: я узнала много новых и интересных методов решения математических задач. А подготовиться я смогла благодаря очень богатому материалу, который хранится на полках нашего математического сообщества, там есть и специальные разделы:
Литература по подготовке к математическим олимпиадам (часть I)
Литература по подготовке к математическим олимпиадам (часть II)
Участие в олимпиаде - это всегда волнительно и ответственно. Каждая решённая задача, это маленькая победа, это маленькое открытие, которое приносит ни с чем несравнимую радость, много положительных эмоций и творческий подъём.
Я очень рада, что мне удалось занять первое место, но если бы я решила всего лишь одну задачу из предложенных, я бы об этом ничуть не пожалела.
Я надеюсь, что эта не последняя математическая олимпиада, и что в будущем ряды желающих участвовать в новых олимпиадах пополнятся.
-
-
27.03.2011 в 16:18-
-
27.03.2011 в 16:21От себя хочу сказать, что просто восхищаюсь и Вашими решениями, и оформлением этих решений.
Прямо жалко, что их увидели только мы.
-
-
27.03.2011 в 16:31Alisa_Selezneva
-
-
27.03.2011 в 16:42А насчёт решений, так это не проблема!
Вот архив: www.onlinedisk.ru/file/634332/
-
-
27.03.2011 в 16:44Нет слов прямо!
Спасибо!
-
-
27.03.2011 в 16:50-
-
27.03.2011 в 18:08?
-
-
27.03.2011 в 20:17Alisa_Selezneva Вы выступили великолепно, получил удовольствие!
-
-
28.03.2011 в 06:42-
-
28.03.2011 в 07:01По 3 задаче никак не предполагал, что производная функции в условии берется по синус в квадрате, а не по х. Если не указано по какой переменной, то надо было бы рассмотреть два варианта.
Поймите меня правильно, это всего лишь маленькие замечания.
-
-
28.03.2011 в 08:02-
-
28.03.2011 в 09:40-
-
28.03.2011 в 09:54Вообще-то следует
-
-
28.03.2011 в 10:10-
-
28.03.2011 в 10:15-
-
28.03.2011 в 10:26-
-
28.03.2011 в 10:39Из-за концов отрезка?
-
-
28.03.2011 в 10:47Они подойдут попозже и все объяснят
-
-
28.03.2011 в 10:50Пусть функция непрерывна на [a, b] и дифференцируема на (a, b). f(a) = f(b), тогда бла-бла-бла.
Так удобнее формулировать
-
-
28.03.2011 в 11:51Остался вопрос по задаче 3 : по какой переменной берется производная в условии задачи, если справа стоит функция от х.
-
-
28.03.2011 в 11:54ну естественно. Я и подчёркивал, что говорится об отрезке и интервале.
по какой переменной берется производная в условии задачи, если справа стоит функция от х.
по иксу
-
-
28.03.2011 в 12:00Остался вопрос по задаче 3 : по какой переменной берется производная в условии задачи, если справа стоит функция от х.
Есть функция `f(x)` мы берем производную по `x` и получаем `f'(x)`.
А потом предоставляем Вам значение производной только, подставив в нее `sin^2(x)` вместо `x`.
Вот и получается `f'(sin^2 x)`.
Например.
`f(x) = x^2; f'(x) = 2*x; f'(sin^2 x) = 2*sin^2(x)`.
-
-
28.03.2011 в 12:27-
-
28.03.2011 в 12:33Нет. Таким образом понять нельзя. Таким образом можно было бы понять, если бы мы записали так: `[f(sin^2(x))]'`.
-
-
28.03.2011 в 12:43Вот здесь Вы ошибаетесь.
`f'(+0)=lim_(x->+0) (f(x)-f(0))/x=lim_(x->+0)(k(x+0.5)-0)/x=k+lim_(x->+0) k/(2x)`. Вы считаете что этот предел существует?
-
-
28.03.2011 в 12:51-
-
28.03.2011 в 12:53