Параметры.

[Afu-Ra]

Здравствуйте, помогите разобраться в задаче.

17. При каких значениях параметра `p` неравентсво

`(x+3p-5)/(x+p)>0`

справедливо для всех `x` таких, что `1<=x<=4`

Решение

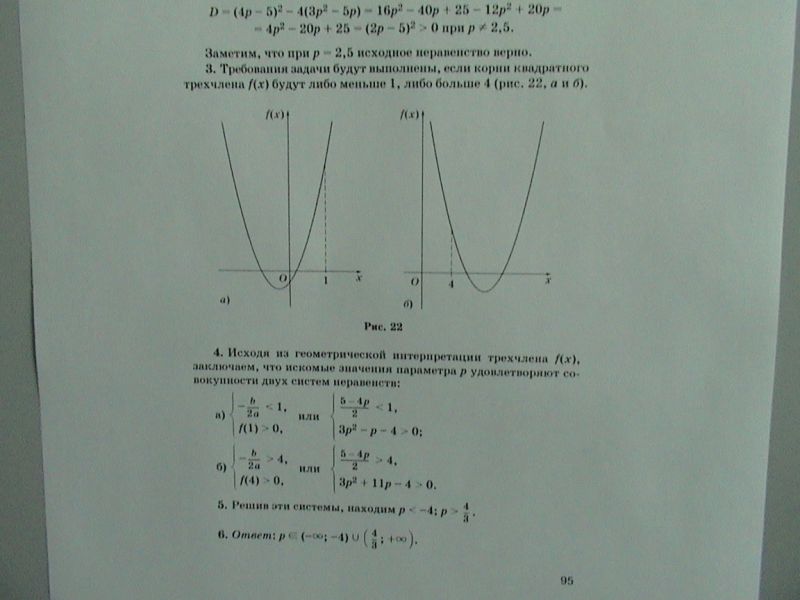
Это решение из книги.

Вопросы.

Вот они из неравенства `(x+3p-5)/(x+p)>0` переходят к равносильному неравенству `(x+3p-5)(x+p)>0`.
У меня вопрос: вот типо подобных неравенств всегда можно переходить к равносильному неравенству, как они сделали?

Дальше я вот понял до того, как они `D` нашли. Но почему он должен быть строго `>0` и, что при `p!=2,5` исходное неравенство верно?

С 3 пункта я уже стал совсем не догонять. Почему корни трехчлена `f(x)` будут меньше 1, либо больше 4? И как они прикинули такой график.

Подскажите пожалуйста.Спасибо.
Конечно, мои вопросы покажутся глупыми кому-то, но я просто хочу разобраться.

@темы: Задачи с параметром

Comments

[Robot]

Да, так как неравенство строгое. неравенство`(P(x))/(Q(x)) > 0` равносильно ` P(x)*Q(x) >0`
Здесь необязательно было переходить к квадратному трехчлену
Можно было просто исследовать с помощью метода интервалов
1)`-p=-3p+5` Исследовать подстановкой `p=5/2`
2)`-p <-3p+5`
Тогда решением неравенства является `(-oo;-p)uu(-3p+5;+oo)
Промежуток [1;4] является решением в случае, если `4 < -p` или `1 > -3p+5`
3)`-p > -3p+5`
...

У меня вопрос: вот типо подобных неравенств всегда можно переходить к равносильному неравенству, как они сделали?

Так как неравенство строгое, то произведение не может быть равно нулю и, следовательно, можно не рассматривать множество допустимых значений знаменателя. Знаки произведения и частного совпадают.

Дальше я вот понял до того, как они `D` нашли. Но почему он должен быть строго `>0` и, что при `p!=2,5` исходное неравенство верно?

После утверждения о том, при `p=2,5` неравенство верно, рассматривают что происходит при `p!=2,5`.

С 3 пункта я уже стал совсем не догонять. Почему корни трехчлена `f(x)` будут меньше 1, либо больше 4?

Если оба корня находятся с одной стороны от отрезка 1;4 и, так как, ветви параболы направлены вверх, то на отрезке 1;4 график фукции будет расположен выше оси ОХ.

[Robot]

В решении на скане рассматривается способ , связанный с расположением квадратного трехчлена относительно промежутка (или относительно конкретного числа)
В ряде пособий это есть
Сначала рассматривается случай, когда график квадратного трехчлена касается оси ОХ (D=0). Вычленяется контрольное значение параметра ипросто проверяется подстановкой
`p=5/2` записывается и решается неравенство, проверяется, содержит ли множество решений промежуток [1;4]
Затем рассматривается случай наличия двух различных корней
Ветви параболы направлены вверх, два корня
А поскольку мн-во решений нер-ва выглядит вот так (выделено красным), как на картинке ниже, то отсюда и следуют дальнейшие рассуждения

Случай отсутствия корней, при котором график распологался бы выше оси ОХ, не рассматривается из-за неотрицательности дискриминанта.

[Afu-Ra]

Щас я прочитаю, осмыслю и если что задам вопросы.

[Afu-Ra]

Вроде стало доходить. Методом интервалов я не очень понял как можно решить, не могли бы вы расписать все поподробнее.
Спасибо за помощь.

[Robot]

Для второго случая

[Afu-Ra]

Честно говоря я понял только то, что надо сначала корни найти `-p` и `-3p+5`.

Если `-p=-3p+5` , то `p=2.5`. Если `p=2.5` подставить в исходное неравенство, то все подходит.

А дальше я непонимаю, как рассуждать.

[Yri]

Решайте это неравенство как Вам советовала Robot методом интервалов.
Как решаете неравенство методом интервалов:
1. Находим нули знаменателя и числителя.
2. Отмечаем их на оси ОX.
3. Находим знаки
Пишем ответ.
В этой задаче то же самое, только корни зависят от параметра, поэтому Вы не знаете, какой из них будет правее, какой левее. Приходится рассматривать 3 случая. Для каждого случая проставляете знаки интервалов, смотрите, куда может попасть отрезок [1; 4], и пишите условие этого (типа `1 > -3p+5` или `4 < -p`.)

А метод, которым разобрана задача в пособии, надо конечно знать. Применяется он довольно часто, обычно в более сложных задачах.

Удачи!

[Afu-Ra]

Вот, например 2 случай, когда `-p<-3p+5`

`p<2.5`

На оси отмечаю точки `-p` и `-3p+5` (слева направо), а дальше как знаки проверять?
Я не могу понять какие вообще значения брать для проверки и подставлять в `(x+3p-5)/(x+p)>0` ?
подскажите, я что-то не могу понять

[Robot]

Никакие знаки не надо проверять
Если вы решаете неравенство (x-3)(x-5) >0 , то решением будет объединение (-oo,3)U(5,+oo)
Это уже должно в крови к 11 классу быть
Неужели вы до сих пор в таком неравенстве точки берете и подставляете?
Если а < b, то решением `(x-a)(x-b) > 0`является (-oo;a)U(b;+00) (в конце концов это один раз продумайте как следует, докажите или же посмотрите по поведению квадратного трехчлена)
Поэтому если `-p <-3p+5`, то решение неравенства заштриховано ниже на рисунке

[Afu-Ra]

В крови бы было если бы школа хорошая была, а то там учат решать то что на 3 . И приходится все самому учиться .

Я понял смысл, что если

Если а < b, то решением `(x-a)(x-b)>0` является (-oo;a)U(b;+00). Я понимаю это.

Ну вот решением неравенства `-p<-3p+5` яв-ся `(-infty;-p)` `uuu` `(-3p+5;+infty)`

`[1;4]` находится в этих промежутках, а дальше как?

[Robot]

Мы ТРЕБУЕМ, чтобы [1;4] в них находился
Это можт быть, если [1;4] находится целиком в левом промежутке. Тогда 4 должно быть меньше -р
Или же он должен целиком находится в правом промежутке
Тогда 1 должно быть больше -3p+5
Вот и получаем что мы должны решить
`{(p <5/2),([(4 <-p),(1> -3p+5):}):}`

[Afu-Ra]

Все я понял, спасибо за помощь.

когда `p<2.5` то `(-infty;-4)

когда `p>2.5` , то `(4/3;+infty)`

[Robot]

Нет
Если вы решаете первую систему (случай p < 5/2), то решением системы будет `(-oo, -4)uu(4/3;5/2)`
Если решаете вторую, то получается (5/2,+оо)
Еще из первого случая р=5/2
И теперь все это объединяем

[Afu-Ra]

А ну да спасибо.