Помогите пожалуйста!!! найти ошибку!

[angel.hall]

Определите множество истинности предиката С(x) ⇒ D(х), заданного на множестве Х={2,5,7,9,11,13,15}, если ТC – простые числа из Х, ТD – простые числа из Х, длящиеся на 5.
решение.

Дано:
С(x) ->D(х)
Х={2,5,7,9,11,13,15}
ТC = {х|х- простые числа } = {2; 5; 7,11,13}
ТD = { ТC ⋮5 } = {5}
Найти: TС(x)->D(х)
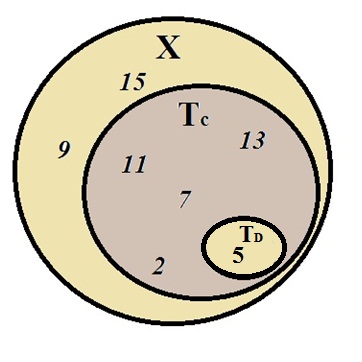
Изобразим данные множества на кругах Эйлера-Венна:

Импликацией предикатов P(x) и Q(x) называется новый предикат , который является ложным при тех и только тех значениях , при которых одновременно P(x) принимает значение “истина”, а Q(x) – значение “ложь”, и принимает значение “истина” во всех остальных случаях.
Поскольку при каждом фиксированном справедлива равносильность

Множество истинности предикатов (неС(х)) это дополнение
ТС(х) до X, полученное удалением из X элементов множества ТС(х) = {2; 5; 7,11,13}. Тогда ТнеС(х)={9; 15}.
Ответ: TС(x)->D(х)= ТнеС U ТD = {9; 15} U{5}={5; 9; 15}.

@темы: Математическая логика, Дискретная математика

Comments

[Robot]

У меня ряд символов не отображается
Но ответ такой же

А есть ошибка?

[angel.hall]

Исправила. А по кругам эйлера, тогда в ответе выбираем {9,15,5}

[Robot]

что по кругам Эйлера, что так — в ответе {9,15,5}={15,5,9}={5,9,15} (это все одно и то же мн-во)
можно просто подставлять значения х
C(2) = > D(2)
2 простое число => 2 делится на 5
и =>л

C(2) = > D(2) - ложное высказывание
и т.д.