Стереометрия

[kiddick]

`TZ` В основании пирамиды лежит равнобедренный треугольник, две стороны которого равны `b`, а угол между ними `alpha`. Одна из боковых граней перпендикулярна плоскости основания, а две другие образуют с основанием двугранные углы, равные `beta` и содержащие данную пирамиду. Какие значения может принимать высота пирамиды? [[/TZ]]

Ну, очевидно, что случая может быть два, в зависимости от выбора равных сторон в треугольнике основания.
Итак, первый случай.
Перпендикулярная грань проходит через основание равнобедренного треугольника.

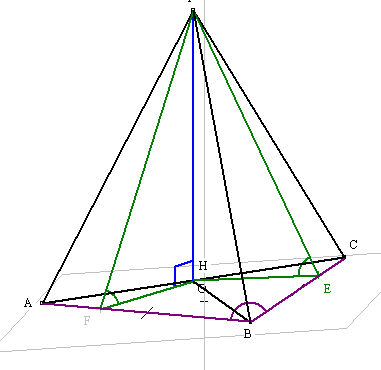
чертеж

зелёным отмечены линейные углы двугранных углов, равные `beta`.
но как доказать, что если провести перпендикуляр к AB в грани ABC и перпендикуляр к AB в грани APB, то они пересекутся в одной точке, а именно в точке F?
а ну да разумеется если две смежные боковые грани пирамиды равнонаклонены к основанию, то вершина пирамиды проецируется на биссектрису угла в основании между этими гранями. вот и жду толчка для окончательного решения. спасибо.
в ответе получается набор из тригонометрических функций. но пока загвоздка в доказательстве.

@темы: Стереометрия

Comments

[Heor]

Теорема о трех перпендикулярах. Как Вариант.

[kiddick]

да слышал о такой, но понимаете в чём дело не выполняется её необходимое и достаточное условие.

[Heor]

kiddick
Не понял. У Вас HF - проекция PF - по условию. AB перпендикулярно к HF. Чего Вам еще не хватает?

[к.черный]

kiddick
я вот тоже не поняла.
Проводите PF _|_ AB, соединяете F и Н,

AB перпендикулярно к HF

по ТТП

[kiddick]

"У Вас HF - проекция PF - по условию" неа, такого у меня в условии нет.
я строил так: в плоскости ABC провёл перпендикуляр к AB через точку H.
в плоскости ABC провёл перпендикуляр к AB через точку H.
в плоскости APB провёл перпендикуляр к AB через точку P. P - вершина пирамиды(вверху там обрезалось)
и так случилось что эти препендикуляры пересеклись в одной точке F.

[к.черный]

"У Вас HF - проекция PF - по условию" неа, такого у меня в условии нет.

отрезок, соединяющий основания перпендикуляра к плоскости и наклонной ЯВЛЯЕТСЯ проекцией наклонной

[kiddick]

ой, видимо я уже переучился, мудрю)

[Heor]

kiddick

и так случилось что эти препендикуляры пересеклись в одной точке F.

Правильно получилось. Вам же уже даже доказали почему.

Я так и не понял чего же Вам не хватает.

[Heor]

"У Вас HF - проекция PF - по условию" неа, такого у меня в условии нет.

Ну если нету, то докажите)

[kiddick]

спасибо, у меня получилась высота `(tg(beta)*sin(alpha))/(2b)`

[kiddick]

пойду думать над вторым случаем.

[к.черный]

у меня получилась высота

b в числителе

[Heor]

kiddick
Такая высота быть не может. Размерность не та...

[kiddick]

во втором случае получилось `tg(beta)sin(alpha)b`
первый пересчитаю сейчас)

[kiddick]

да, в первом я нашёл ошибку, `b` в одном месте в сомножителях потерял) спасибо!

[kiddick]

если не сложно, проверьте второй случай)

[kiddick]

[Heor]

kiddick
Второй не верен.

[kiddick]

как же так?
вот треугольник в основании, нашёл LH, получилось `sin(alpha)b`

[Heor]

kiddick
А с чего Вы взяли, что BH равно `b`?

[kiddick]

машинально как то так получилось

[kiddick]

[Heor]

kiddick
Ну и? Теперь рисунок правильный. А ответ будете исправлять?

[kiddick]

хм, так сложнее, для того чтобы найти LH мне надо найти BH. чтото я не представляю пока как это сделать.

[к.черный]

я сделала через площади.
Биссектриса СН разделила тр-к АВС на два тр-ка с площадями S1 и S2
S1/S2=BH/HA=CB/CA
S1+S2=S(ABC)

[kiddick]

`BH=b/(1+sqrt(2(1-cosa)))

[Heor]

kiddick
Через уравнение, например. Пусть `BH=x`, тогда `HL = ...` и `HS = ` и т.к. обе плоскости составляют угол `beta` с основанием, то ...

Или докажите, что `CH` - биссектриса. И воспользуйтесь одним из свойств биссектрисы.

[kiddick]

`b/(2 sin(a/2)+1)` как моё выражение привести к такому виу?

[kiddick]

а всё нашёл формулу)

[к.черный]

это что? И что за

моё выражение

?