Задачи по геометрии

[Dante<3]

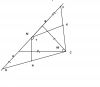
1) `TZ`В треугольнике ABC угол при вершине C равен 60. На продолжении стороны AB за точку A отмечена точка D такая, что AD=BC, а на продолжении AB за точку B отмечена точка F такая, что BF=AC. Точки N, M, K – середины отрезков CD, AB, CF соответственно. Найдите величину угла NMK.[[/TZ]]

2)`TZ`На сторонах AB и CD квадрата ABCD отмечены точки M и N соответственно. Отрезки CM и BN пересекаются в точке P, а отрезки AN и MD – в точке Q. Докажите, что |PQ|>=1\2|AB|.[[/TZ]]


Решал вторую задачу, смогу доказать, что если M середина AB, то |PQ|=1\2|AB|, пробовал доказывать, что при других случаях |PQ|>1\2|AB| через вектора, но не получается.

@темы: Планиметрия

Comments

[Heor]

Dante<3
Начните с рисунков.

[Dante<3]

А как же еще решать задачи по геометрии не рисуя? Рисунки есть.

[Robot]

Dante<3По правилам рекомендуется выкладывать их, чтобы они и у нас были перед глазами

[Heor]

Рисунки есть.

Я, наверное, ослеп. Не вижу, к сожалению.

[Dante<3]

Первая

Вторая

[Robot]

следующим комментом дам подсказку

[Robot]

Угол, который надо найти, разбивается на три угла отрезками МЕ и МG
1)Подумайте, чем для треугольника АВС является EG
2) что можно сказать про длины NE и EM, МG и GK
3)из этого будет следовать равенство нескольких углов
4)чем является MEСG и какое свойство этого чет-ка тогда можно использовать
5) в конце я использовала, что угол АМВ развернутый

[Dante<3]

1) Средней линией что-ли? Если это она то, как доказать, что это она?

[Heor]

Dante<3
1. Верно. А чем является NK для DCF? И каким свойством обладает?

[Dante<3]

Тоже средняя линия, параллельна основанию и 1\2 основания вроде, ну и CNK ~ DCF

[Heor]

Dante<3
Это все верно, вот только это еще не все. Подумайте над тем, как делит NK любой отрезок CQ, если `Q in DF` (Q лежит на отрезке DF).
Впрочем, это можно доказать (вывести) и из подобия треугольников.

[Robot]

Я так понимаю, что мы над первым пунктом сидим?
NK||DF(DA) и N -середина CD, значит, Е - середина АС (то что NE - средняя линия в треугольнике DCA нам тоже пригодится)

[Dante<3]

Теперь тоже самое с ABC? Ну тогда ясно.
2) NE=EM, MG=GK,(только опять же, почему они равны?) тогда эти треугольники равнобедренные и <N=

[Robot]

Dante<3
Отделяйте < и > пробелами

2) NE=EM, MG=GK,(только опять же, почему они равны?)

Мы не предоставляем полных решений
основные идеи я высказала
обозначьте стороны треугольника АВС a,b,c, найдите равные им отрезки
Точки E, G, М середины сторон треугольника АВС - используйте и эти факты
Там куча средних линий

[Dante<3]

Спасибо и на этом, а вторую вы не пробовали осилить?

[Robot]

Dante<3
И на этом? хм-м..
Нет, вы еще не решили первую
А вопросов в сообществе слишком много