Осталось решить всего 2 предела
В номере 19-ть скорее всего надо свести к 2-му замечательному (предположительно там ответ е/3)
В 20-м вообще не понимаю как подступиться(
Посоветуйте что-нибудь!
Заранее спасибо!
воскресенье, 11 апреля 2010
Осталось решить всего 2 предела
В номере 19-ть скорее всего надо свести к 2-му замечательному (предположительно там ответ е/3)
В 20-м вообще не понимаю как подступиться(
Посоветуйте что-нибудь!
Заранее спасибо!
В угол , равный arccos (-1/9), вписана окружность радиуса 3. Параллельно хорде, соединяющей точки касания , проведены две касательные к окружности , в результате чего получилась трапеция. Найдите площадь этой трапеции.
Я решение прикрепил, скажите ка кделать прально или где у меня переделать
суббота, 10 апреля 2010
1)Вычислить площадь фигур, ограниченной прямыми и кривыми: х=0, у=2^х, х=2, н=2х-х^2
2)Найти объёмы тел, образованных вращением элипса вокруг осей Ох и Оу х^2/а^2 + у^2/b^2=1
3) найти координаты центратяжести фигуры, ограниченной дугой элипса х=а соst , y=b sint располож. в первой четверти , и осями координат
Не могу решить!! Заранее спасибо)))
2)Найти объёмы тел, образованных вращением элипса вокруг осей Ох и Оу х^2/а^2 + у^2/b^2=1
3) найти координаты центратяжести фигуры, ограниченной дугой элипса х=а соst , y=b sint располож. в первой четверти , и осями координат
Не могу решить!! Заранее спасибо)))
Вот предел:
Не знаю, как подступиться.. Пробовал заменой - ни к чему не привело( Пробовал привести к формулам приведения, опять же ни к чему считаемому не привело..
Подскажите, пожалуйста, каким способом его решать?
Не знаю, как подступиться.. Пробовал заменой - ни к чему не привело( Пробовал привести к формулам приведения, опять же ни к чему считаемому не привело..
Подскажите, пожалуйста, каким способом его решать?
Прошу посоветовать мне книгу с примерами типовых задач на Преобразование Лапласа. Спасибо.
Не трать впустую (с)
Даже не знаю, к какому разделу отнести эти вопросы... Буду очень признательна, если посоветуете какую-нибудь литературу на эту тему или подскажете:
1) Существует ли признак Абеля для повторных рядов? Или что-то вроде аналога признака Абеля.
2) Что значит термин "кусочно-непрерывная функция на торе"? Т.е., конечно, на торе такого понятия нет, но есть ли аналог с такими же свойствами, или какая-нибудь специальная формулировка для этих функций:
3) Какие необходимые условия для разложения таких функций в ряд Фурье? Для обычных кусочно-непрерывных есть теоремка для разложение в ряд Фурье, а для "кусочно непрерывных на торе"?
1) Существует ли признак Абеля для повторных рядов? Или что-то вроде аналога признака Абеля.
2) Что значит термин "кусочно-непрерывная функция на торе"? Т.е., конечно, на торе такого понятия нет, но есть ли аналог с такими же свойствами, или какая-нибудь специальная формулировка для этих функций:
3) Какие необходимые условия для разложения таких функций в ряд Фурье? Для обычных кусочно-непрерывных есть теоремка для разложение в ряд Фурье, а для "кусочно непрерывных на торе"?
помогите пожалуйста, не знаю с чего начать....
Я поджарю врага. А ты пока поджарь мне рыбки. К завтраку я вернусь. (с)
У кого-нибудь есть русский хелп по маткаду?
Помогите решить ,это задача В9.12. В основании прямой призмы лежит прямоугольный треугольник с катетами 7 и 8. Боковые ребра равна 8/п.Найдите объем цилиндра, описанного около этой призмы.
я нашла решение на сайте profmeter.com.ua/communication/learning/course/...
Решение.
Найдем диагональ основания призмы, исходя из информации о размере ребер ее основания.
По теореме Пифагора, найдем квадрат гипотенузы треугольника, лежащего в основании.
72 + 82 = 113
Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
Таким образом, цилиндр, описанный около заданной призмы, будет иметь диаметр, равный гипотенузе прямоугольного треугольника, лежащего в основании призмы и высоту, равную высоте призмы. Таким образом, объем цилиндра составит:
V= пr^2h, гдепr
п - число пи
r - радиус основания цилиндра
h - высота цилиндра
Поскольку гипотенуза прямоугольного треугольника, лежащего в основании призмы одновременно является диаметром цилиндра, описанного вокруг призмы, то радиус цилиндра будет равен половине гипотенузы, то есть квадратный корень из 113 деленный пополам, а квадрат радиуса, соответственно равен r^2=113/4.
По условию задачи высота ребра призмы равна 8/п .
Таким образом:
V=п*113/4*8/п
V=226
Ответ: 226
я нашла решение на сайте profmeter.com.ua/communication/learning/course/...
Решение.
Найдем диагональ основания призмы, исходя из информации о размере ребер ее основания.
По теореме Пифагора, найдем квадрат гипотенузы треугольника, лежащего в основании.
72 + 82 = 113
Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
Таким образом, цилиндр, описанный около заданной призмы, будет иметь диаметр, равный гипотенузе прямоугольного треугольника, лежащего в основании призмы и высоту, равную высоте призмы. Таким образом, объем цилиндра составит:
V= пr^2h, гдепr
п - число пи
r - радиус основания цилиндра
h - высота цилиндра
Поскольку гипотенуза прямоугольного треугольника, лежащего в основании призмы одновременно является диаметром цилиндра, описанного вокруг призмы, то радиус цилиндра будет равен половине гипотенузы, то есть квадратный корень из 113 деленный пополам, а квадрат радиуса, соответственно равен r^2=113/4.
По условию задачи высота ребра призмы равна 8/п .
Таким образом:
V=п*113/4*8/п
V=226
Ответ: 226
Здесь мне помогут с вычислениями в программе Maple?
Найдите все такие значения параметра a, для которых уравнение 2х-|2x-|x+a||=3|x-2| имеет ровно два корня.
Подскажите пожалуйста...
Подскажите пожалуйста...
Подскажите, как действовать в данном пределе:
Заранее спасибо!
Заранее спасибо!
Keep us all dumbed down and hope that we will never see the truth around(Muse is <3)
Добрый день!
Пожалуйста, помогите разобраться с заданием.
Алгебра, 9ый класс, домашняя самостоятельная работа(сказали, что по сути олимпиадные задания).
Найдите четыре числа, из которых первые три составляют геометрическую прогрессию, а последние три - арифметическую, если сумма крайних чисел равна 32, а сумма средних чисел равна 24.
Ходят слухи, что решается через системы уравнений. Пожалуйста, подскажите хоть идею, как это начать, придумать.
Крайний срок - вечер воскресенья, в понедельник сдавать.
Заранее спасибо,
Ася.
Пробовал свести к пределу ln(1+x)/x, но ни к чему это не привело..
Не подскажите, как действовать в данном случае?
Основанием пирамиды служит квадрат, две боковые грани этой пирамиды перпендикулярны к плоскости ее основания , две другие ее боковые грани образуют с плоскостью основания равные двугранные углы , каждый из которых равен 30. Высота пирамиды равна sqrt(2). Найдите площадь боковой поверхности пирамиды.
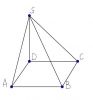
Помогите разобраться....
Помогите разобраться....
Здравствуйте. помогите пожалуйста решить задачу. Задание : В трапеции, боковые стороны которой равны 5 и 8, вписана окружность радиуса 2. Найти площадь трапеции.
Добрый день!
Помогите, пожалуйста, решить задачку.
Если вектор |a|= sqrt(5), |b|=2, |a+b|= sqrt(11), то скалярное произведение (2a-b)(a+3b) равно: 1)-3 2)-2 3)2 4)3 5)6
Помогите, пожалуйста, решить задачку.
Если вектор |a|= sqrt(5), |b|=2, |a+b|= sqrt(11), то скалярное произведение (2a-b)(a+3b) равно: 1)-3 2)-2 3)2 4)3 5)6
Если у вас установлена Java, то смотрите модель. к задаче.
10.04.2010 в 12:17
Пишет Trotil:Место одно и тоже.
Место одно и тоже.
Сначала на нём стоял путник с посохом (именуемый также «вечным студентом», а в шутку, за похожесть под определенным углом зрения, — «Раздавленным Жуком»), у подножия которого была начертана фраза «Дорогу осилит идущий». Эта фраза многими считалась девизом МИФИ. Теперь там крест. Памятник, как считается, поставили к приезду патриарха. Неофициальное название "Крест на российской науке". Остальное написано здесь.
URL записиМесто одно и тоже.
Сначала на нём стоял путник с посохом (именуемый также «вечным студентом», а в шутку, за похожесть под определенным углом зрения, — «Раздавленным Жуком»), у подножия которого была начертана фраза «Дорогу осилит идущий». Эта фраза многими считалась девизом МИФИ. Теперь там крест. Памятник, как считается, поставили к приезду патриарха. Неофициальное название "Крест на российской науке". Остальное написано здесь.
Помогите
1)В буфете составляется всевозможные наборы по 3 пироженных 12 разных сортов(сорты могут и повторяться). Сколько наборов придется составить??
2)Пространство U содержить 19 элементарных исходов.Известно что благоприятно для :
A-3
B-7
C-4
A*B-1
B*C-3
A*C-Не сущ
Найти A+A*B+(A) где (A)-это A с верхней чертой тоесть противоположно A
3)Решить с помощью геометрической вероятности
Коэффициенты p и q квадратного уравнения x^2+p*x+q=0 заключены между [-1;3].Найти вероятность того,что корни уравнения со случайно выбранными коэффициентами p и q положительны.
4)Использовать сложение вероятностей
Двое поочередно бросают монету до первого выпадания.Найти вероятность того что в первый раз герб появиться у первого.
5)Применить локальную или интегральную теорему Муавро-Лапласа или Теорему Пуассона
Найти вероятность того что при 100 бросании монеты герб выпадет 50 раз
6)Ряд распределения дискретной случайной величины
Бросают две кости.Построить ряд распределения суммы чисел выпавших очков
Заранее благодарен!!
у меня получилось решить первою
Выборка с возвращение , не упорядочная
С =12!/(3!*9!)=220
Вторую там как я понял т.к A и (A) то события охватывает все 19.
Пятая там по формуле Муавра-Лапласа получилось 0.0798
Проверьте правильно или нет
А вот что делать с геометрической вероятностью я не знаю. Помоги плз
1)В буфете составляется всевозможные наборы по 3 пироженных 12 разных сортов(сорты могут и повторяться). Сколько наборов придется составить??
2)Пространство U содержить 19 элементарных исходов.Известно что благоприятно для :
A-3
B-7
C-4
A*B-1
B*C-3
A*C-Не сущ
Найти A+A*B+(A) где (A)-это A с верхней чертой тоесть противоположно A
3)Решить с помощью геометрической вероятности
Коэффициенты p и q квадратного уравнения x^2+p*x+q=0 заключены между [-1;3].Найти вероятность того,что корни уравнения со случайно выбранными коэффициентами p и q положительны.
4)Использовать сложение вероятностей
Двое поочередно бросают монету до первого выпадания.Найти вероятность того что в первый раз герб появиться у первого.
5)Применить локальную или интегральную теорему Муавро-Лапласа или Теорему Пуассона
Найти вероятность того что при 100 бросании монеты герб выпадет 50 раз
6)Ряд распределения дискретной случайной величины
Бросают две кости.Построить ряд распределения суммы чисел выпавших очков
Заранее благодарен!!
у меня получилось решить первою
Выборка с возвращение , не упорядочная
С =12!/(3!*9!)=220
Вторую там как я понял т.к A и (A) то события охватывает все 19.
Пятая там по формуле Муавра-Лапласа получилось 0.0798
Проверьте правильно или нет
А вот что делать с геометрической вероятностью я не знаю. Помоги плз