Я одна, но всё же я есть. Я не могу сделать всё, но всё же могу сделать что-то. И я не откажусь сделать то немногое, что могу (c)
Ященко И. В., Шестаков С. А., Захаров П. И. Подготовка к ЕГЭ по математике в 2010 году. Методические указания. -М., МЦНМО, 2009. - 128 с.
ДР № 5 С2
С2. Ребро AD пирамиды DABC перпендикулярно плоскости основания ABC. Найдите расстояние от вершины А до плоскости, проходящей через середины ребер АВ, АС и AD, если AD = 2√5, АВ = АС =10, ВС = 4√5
Решение.
Построение сечения трудностей не вызывает
 ">
">
Задачу можно решать двумя способами
1 способ. Расстояние от А до плоскости сечения равно высоте пирамиды АEFG с вершиной А и основанием EFG, а потому можно найти двумя способами объем этой пирамиды как ЕАFG и как АEFG;
2 способ. Очевидно, что AF=AG, а в силу равенства прямоугольных треугольников AEF и AEG имеем GE=GF. Путь Н - середина GF. ЕН - высота и медиана в равнобедренном треугольнике GEF и АН - высота и медиана в равнобедренном треугольнике AFG. Значит, FG перпендикулярна двум пересекающимся прямым ЕН и АН плоскости ЕНА, то есть FG перпендикулярна и самой этой плоскости а следовательно, и любой прямой в этой плоскости.
Проведем в плоскости ЕАН АК⊥ЕН. Тогда по вышесказанному АК⊥FG и АК⊥ЕН. то есть АК -перпендикуляр к плоскости сечения. Найдем его длину
С помощью теоремы Пифагора находим АН=2√5, EG=√30, EH = 5. Используя далее метод площадей, получаем АК*ЕН=АЕ*АН, отсюда АК=2
Ответ: 2
ДР № 6 С2
В пирамиде DABC известны длины ребер: АВ = АС = DB = DC= 10, BC = DA= 12. Найдите расстояние между прямыми DA и ВС.
Решение.

Расстояние между скрещивающимися пряыми можно найти, как длину их общего перпендикуляра.
Пусть Е - середина AD, Н середина ВС. Соединим Е и Н.
Так как АВ=АС, то треугольник АВС равнобедренный и медиана АН одновременно является и высотой. Аналогично и с треугольником DBC - DH является в нем медианой и высотой. А потому ВС⊥АН и ВС⊥DH, а значит, ВС перпендикулярен плоскости ADH, следовательно и любой прямой в этой пл-ти.Таким образом , ЕН⊥ВС.
Так как треугольники АВС и DBC равны, то равны и АН и DH, а поэтому ЕН - медиана и высота в равнобедренном треугольнике АHD, а потому ЕН⊥AD.
Поэтому ЕН - общий перпендикуляр к скрещивающимся прямым. Используя теорему Пифагора, получаем, что ЕН=2√7
ДР № 7 С2
С2. Основанием прямой треугольной призмы АВСА1В1С1 является равнобедренный треугольник ABC, в котором АВ = ВС = 10, АС = 16. Боковое ребро призмы равно 24. Точка Р — середина ребра ВВ1. Найдите тангенс угла между плоскостями А1В1С1 и АСР.
Решение

Так как плоскости АВС и А1В1С1 параллельны, то найдем угол между плоскостью АСР и плоскостью АВС. Пусть D - середина АС. Так как треугольники АВМ и АСР равнобедренные, то РD и ВD перпендикуляры к АС (линии пересечения плоскостей АСР и АСВ). Тогда угол РDВ - искомый. Его тангенс равен ВР/ВD, где ВD находится по теореме Пифагора ВD=6. Отсюда tgРDВ=12/6=2
ДР № 8 С2
Дан куб АВСDA1B1C1D1. найдите угол между плоскостями АВ1С1 и А1В1С
Решение

Будем искать угол между плоскостями через угол между перпендикулярными им прямыми.
Для плоскости АВ1С1 такой прямой является D1C. Действительно, так как диагнали квадрата перпендикулярны, то D1С⊥C1D. Кроме того по теореме о трех перпендикулярах D1С⊥AD. Значит, D1C перпендикуляр к плоскости АВ1С1.
Аналогично AD1 - перпендикуляр к плоскости А1В1С.
Найдем угол между прямыми D1C и AD1
Рассмотрим треугольник AD1C - он правильный, так как его сторонами являются диагонали граней куба. Поэтому искомый угол равен П/3
Ответ: П/3
ДР № 9 С2
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины ребер: АА1= 5, АВ = 12, AD = 8. Найдите тангенс угла между плоскостью ABC и плоскостью, проходящей через точку В перпендикулярно прямой АК, если К — середина ребра C1D1.
Решение

Как и выше, будем искать угол между плоскостями, как угол между перпендикулярными им прямыми. Для плоскости АВС такой прямой является прямая КЕ||DD1. Для второй плоскости по условию такой прямой является АК. Искомый угол - угол АКЕ.
Рассмотрим треугольник АКЕ. КЕ=5, АЕ находится легко с помощью теоремы Пифагора из треугольника ADE АЕ=10.
Тогда tg∠АКЕ=2
ДР № 5 С2
С2. Ребро AD пирамиды DABC перпендикулярно плоскости основания ABC. Найдите расстояние от вершины А до плоскости, проходящей через середины ребер АВ, АС и AD, если AD = 2√5, АВ = АС =10, ВС = 4√5
Решение.
Построение сечения трудностей не вызывает
 ">
">Задачу можно решать двумя способами
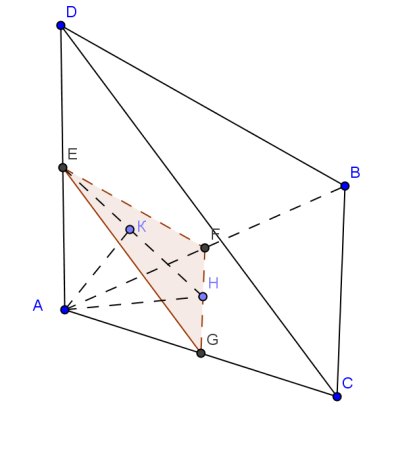
1 способ. Расстояние от А до плоскости сечения равно высоте пирамиды АEFG с вершиной А и основанием EFG, а потому можно найти двумя способами объем этой пирамиды как ЕАFG и как АEFG;
2 способ. Очевидно, что AF=AG, а в силу равенства прямоугольных треугольников AEF и AEG имеем GE=GF. Путь Н - середина GF. ЕН - высота и медиана в равнобедренном треугольнике GEF и АН - высота и медиана в равнобедренном треугольнике AFG. Значит, FG перпендикулярна двум пересекающимся прямым ЕН и АН плоскости ЕНА, то есть FG перпендикулярна и самой этой плоскости а следовательно, и любой прямой в этой плоскости.
Проведем в плоскости ЕАН АК⊥ЕН. Тогда по вышесказанному АК⊥FG и АК⊥ЕН. то есть АК -перпендикуляр к плоскости сечения. Найдем его длину
С помощью теоремы Пифагора находим АН=2√5, EG=√30, EH = 5. Используя далее метод площадей, получаем АК*ЕН=АЕ*АН, отсюда АК=2
Ответ: 2
ДР № 6 С2
В пирамиде DABC известны длины ребер: АВ = АС = DB = DC= 10, BC = DA= 12. Найдите расстояние между прямыми DA и ВС.
Решение.

Расстояние между скрещивающимися пряыми можно найти, как длину их общего перпендикуляра.
Пусть Е - середина AD, Н середина ВС. Соединим Е и Н.
Так как АВ=АС, то треугольник АВС равнобедренный и медиана АН одновременно является и высотой. Аналогично и с треугольником DBC - DH является в нем медианой и высотой. А потому ВС⊥АН и ВС⊥DH, а значит, ВС перпендикулярен плоскости ADH, следовательно и любой прямой в этой пл-ти.Таким образом , ЕН⊥ВС.
Так как треугольники АВС и DBC равны, то равны и АН и DH, а поэтому ЕН - медиана и высота в равнобедренном треугольнике АHD, а потому ЕН⊥AD.
Поэтому ЕН - общий перпендикуляр к скрещивающимся прямым. Используя теорему Пифагора, получаем, что ЕН=2√7
ДР № 7 С2
С2. Основанием прямой треугольной призмы АВСА1В1С1 является равнобедренный треугольник ABC, в котором АВ = ВС = 10, АС = 16. Боковое ребро призмы равно 24. Точка Р — середина ребра ВВ1. Найдите тангенс угла между плоскостями А1В1С1 и АСР.
Решение

Так как плоскости АВС и А1В1С1 параллельны, то найдем угол между плоскостью АСР и плоскостью АВС. Пусть D - середина АС. Так как треугольники АВМ и АСР равнобедренные, то РD и ВD перпендикуляры к АС (линии пересечения плоскостей АСР и АСВ). Тогда угол РDВ - искомый. Его тангенс равен ВР/ВD, где ВD находится по теореме Пифагора ВD=6. Отсюда tgРDВ=12/6=2
ДР № 8 С2
Дан куб АВСDA1B1C1D1. найдите угол между плоскостями АВ1С1 и А1В1С
Решение

Будем искать угол между плоскостями через угол между перпендикулярными им прямыми.
Для плоскости АВ1С1 такой прямой является D1C. Действительно, так как диагнали квадрата перпендикулярны, то D1С⊥C1D. Кроме того по теореме о трех перпендикулярах D1С⊥AD. Значит, D1C перпендикуляр к плоскости АВ1С1.
Аналогично AD1 - перпендикуляр к плоскости А1В1С.
Найдем угол между прямыми D1C и AD1
Рассмотрим треугольник AD1C - он правильный, так как его сторонами являются диагонали граней куба. Поэтому искомый угол равен П/3
Ответ: П/3
ДР № 9 С2
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины ребер: АА1= 5, АВ = 12, AD = 8. Найдите тангенс угла между плоскостью ABC и плоскостью, проходящей через точку В перпендикулярно прямой АК, если К — середина ребра C1D1.
Решение

Как и выше, будем искать угол между плоскостями, как угол между перпендикулярными им прямыми. Для плоскости АВС такой прямой является прямая КЕ||DD1. Для второй плоскости по условию такой прямой является АК. Искомый угол - угол АКЕ.
Рассмотрим треугольник АКЕ. КЕ=5, АЕ находится легко с помощью теоремы Пифагора из треугольника ADE АЕ=10.
Тогда tg∠АКЕ=2




-
-
06.11.2009 в 00:30Кстати - как красиво получается искать углы между перпендикулярами
Распространенный в С2 прикол
-
-
06.11.2009 в 00:34Это я просто валялась в постели и решала, а как немножко температура спала, оформила. Сейчас опять завалюсь.
Боюсь ошибок/опечаток там много, надо смотреть
-
-
06.11.2009 в 00:35Ага))
чУдный способ!
-
-
06.11.2009 в 03:54Robot Выздоравливайте скорее
-
-
06.11.2009 в 16:20-
-
23.11.2009 в 20:17-
-
23.11.2009 в 20:38-
-
25.01.2010 в 18:39-
-
26.01.2010 в 22:21-
-
26.01.2010 в 23:07Метод площадей заключается в том, что мы площадь треугольника АЕН находим 2 способами и приравниваем
(1/2)АК*ЕН=(1/2)АЕ*АН
-
-
31.01.2010 в 22:34-
-
31.01.2010 в 22:36-
-
16.02.2010 в 20:17-
-
19.02.2010 в 18:09-
-
19.02.2010 в 18:13Этот топик посвящен С2, С3 можно скачать отсюда www.alexlarin.narod.ru/ege.html
Если останутся вопросы, то в левом столбце Написать в сообщество и эти вопросы задайте
-
-
11.03.2010 в 08:26-
-
11.03.2010 в 08:55-
-
04.05.2010 в 23:59-
-
22.03.2012 в 21:57-
-
22.03.2013 в 18:20-
-
15.05.2013 в 17:26-
-
15.05.2013 в 17:27По какому учебнику обучаетесь?
-
-
22.05.2013 в 00:22-
-
22.02.2014 в 10:58-
-
22.02.2014 в 11:33Создайте новый топик с этой задачей
-
-
26.04.2014 в 16:52-
-
20.04.2015 в 17:56