[Amicus Plato]

На мой взгляд, математику, в той степени, в которой он математик, нет нужды заниматься философией — более того, этого мнения придерживаются и многие философы. Анри Лебег. Scientific American 211 (September 1964)

Сегодня, 28 июня, день рождения у выдающегося французского математика Анри Леона Лебега. В этом году ему исполнилось 140 лет.

Анри Леон Лебег (фр. Henri Léon Lebesgue; 28 июня 1875, Бове, департамент Уаза — 26 июля 1941, Париж) — французский математик, член Парижской АН (1922), член-корреспондент АН СССР (1929). Профессор Парижского университета (с 1910).

Биография
Биографию я цитирую не по Википедии. Я ее взяла с этого сайта, но на самом деле она во многих местах встречается ровно такая. Поэтому авторства не знаю...
Анри Лебег родился 28 июня 1875 г. в семье рабочего типографии города Бове, расположенного вблизи Парижа. Отец его был человеком просвещенным. Мать работала преподавателем начальной школы. У них была строго подобоанная домашняя библиотека, которая сыграла не последнюю роль в приобщении мальчика к миру точных наук. Отец рано умер, и только предоставление Анри Леону стипендии муниципалитетом Бове позволило ему, по завершению начального образования, учится в городском колледже. Девятнадцати лет Анри Лебег поступил в Начальную школу. По окончании в 1897 г. института Лебег получил квалификацию преподавателя средней школы по математическим предметам. Он, однако, остался в Нормальной школе еще на два года помощником библиотекаря, чтобы иметь свободный доступ к интересующей его научной литературе и время для ее глубокого изучения. Он действительно овладел многими вопросами старых и новых разделов классического анализа по первоисточникам. Особое внимание Лебег уделял началам теории спрямления кривых и квадратуры поверхностей и уже возникшим в них коренных проблемам и противоречиям из-за несоответствия примитивных функций неопределенным интегралам. Проблемы кратного интегрирования и теоретико-множественный подход к ним, тригонометрические ряды и невозможность безоговорочного интегрирования рядов с ограниченными в совокупности членами, специальное изучение интегралов Дарбу и представление непрерывных функций неопределенными интегралами — все оказалось в поле зрения исследователя. С 1899 г. Лебег в течение трех лет работал преподавателем математики в Центральном лицее г. Нанси.
Сразу после защиты докторской диссертации, в 1902 г. он прибыл на работу в университет г. Рена. Там он читает лекции на медицинском факультете. В это же время его приглашают прочитать лекции в Колледж де Франс, что явилось начало признаний его научных заслуг. В 1906 г. Лебег прошел по конкурсу университета г. Пуатье на должность доцента. В этом же году он становиться профессором университета. В 1903 - 1910 гг.— наиболее плодотворный период в жизни Лебега. За эти годы опубликована почти треть всех его научных трудов. В 1910 г. Лебег был приглашен в Парижский университет. До 1919 г. он работает там лектором на естественном факультете Сорбонны, а в 1920 г. был избран профессором этого факультета. 1912 г. явился годом официального признания научных заслуг Лебега Французской академией наук. Во время первой мировой войны, являясь председателем математической комиссии Службы изобретений, образования и научного эксперимента, Лебег решил проблему определения и уточнения траекторий снарядов. Под его руководством был составлен сборник траекторий. За все это он был награжден орденом Почетного легиона.
В 1921 г. Лебег покидает Сорбонну. Он был избран профессором Колледж де Франс. Здесь он принял меры к модернизации классических учебных курсов по математике, к их обновлению в свете новейших теорий. С 1922 г. начинается академическая деятельность Лебега. В этом году он удостоился чести быть выбранным в Парижскую Академию наук вместо умершего К. Жордана. Анри Лебег был прекрасным отцом и хорошим мужем. У него было двое детей — дочь Сюзанна и сын Жак. В 1940 г. во время второй мировой войны родной дом Лебега в г. Бове был разрушен. Еще более ощутимым ударом, от которого математик уже не смог оправиться, явилась фашистская оккупация Франции, что глубоко уязвило чувство национальной гордости Лебега; он замкнулся в себе. Мрачная действительность способствовала обострению его болезни. 26 июля 1941 г. его не стало.

Достижения в математике
Первые исследования Лебега касались рядов Фурье. Позже он заинтересовался теорией интегрирования. Лебег считается одним из основателей современной теории функций действительной переменной. Создал теорию меры, внедрил понятие измеримой функции, ввел новое определение интеграла (интеграл Лебега), благодаря чему стало возможным интегрирование чрезвычайного широкого класса функций. Исследовал возможность аналитического изображения функций. Написал работы по теории размерности; доказал существование функций всех классов классификации Бэра; получил важные результаты геометрического и топологического характера; занимался исследованиями по вопросам теории функций, множеств и теории дифференцирования. В теории функций и в функциональном анализе широко известны такие понятия, как мера Лебега, интеграл Лебега, интеграл Лебега-Стилтьеса, лебеговские множества.

Интеграл Лебега
Интеграл Лебега — это обобщение интеграла Римана на более широкий класс функций.
Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла равны. Однако существует большой класс функций, определённых на отрезке и интегрируемых по Лебегу, но неинтегрируемых по Риману. Также интеграл Лебега может иметь смысл для функций, заданных на произвольных множествах (интеграл Фреше).
Идея построения интеграла Лебега состоит в том, что вместо разбиения области определения подынтегральной функции на части и составления потом интегральной суммы из значений функции на этих частях, на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.

Сверху интегрирование по Риману, снизу по Лебегу

А вот еще в качестве бонуса картинка из некоей Энциклобогии:

Интеграл Лебега, застигнутый на месте интегрирования. Трофей: сборник задач Демидовича

Задача Лебега
Задача Лебега состоит в отыскании плоской фигуры наименьшей площади, которая способна накрыть собой любую плоскую фигуру диаметра 1.
Замечание
Любая фигура диаметра 1 может быть накрыта фигурой постоянной ширины 1 (каждая фигура диаметра 1 — своей фигурой постоянной ширины, то есть фигура постоянной ширины зависит от фигуры диаметра 1). Для фигур постоянной ширины, диаметр совпадает с шириной. Поэтому задача Лебега сводится к нахождению плоской фигуры наименьшей площади, которая способна накрыть собой фигуру постоянной ширины 1.

Замечание в замечании
Кривая постоянной ширины `a` — плоская выпуклая кривая, длина ортогональной проекции которой на любую прямую равна a.
Иными словами, кривой постоянной ширины называется плоская выпуклая кривая, расстояние между любыми двумя параллельными опорными прямыми которой постоянно и равно `a` — «ширине» кривой.

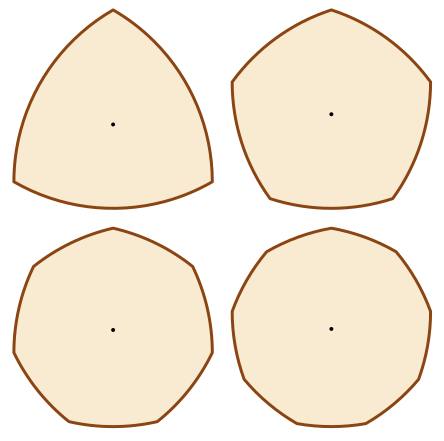
Примеры

Треугольник Рёло - кривая постоянной ширины. Стороны квадрата - опорные прямые: каждая сторона касается треугольника, но не пересекает его. Треугольник Рёло можно вращать, и при этом он всегда будет касаться каждой стороны квадрата; таким образом ширина треугольника (расстояние между двумя опорными прямыми) постоянна.

Известно, что фигура Лебега существует, но она, возможно, не единственна. Если `L` её площадь, то известно, что
`0,826 < L < 0,845`.

Ссылки
1. Снова интересная статья на сайте, который я уже неоднократно рекомендовала math4school.ru.
2. Лебег А.Л. Об измерении величин. [Djv-ZIP] Перевод под редакцией А.Н.Колмогорова. (Москва: Учпедгиз, 1938). Книга
3. Тумаков И.М. Анри Леон Лебег. 1875-1941 [Djvu] М.: Наука, 1975. — 120 с. Книга

@темы: История математики, Люди

Comments

[All_ex]

Amicus Plato, Спасибо ...

Вспомнилась ещё такая картинка ... была в задаче ЧГК ...