Простыми словами
25 января исполнилось 145 лет со дня рождения Нильса Фабиана Хельге фон Коха.

Википедия
Нильс Фабиан Хельге фон Кох (швед. Niels Fabian Helge von Koch, 25 января 1870 — 11 марта 1924) — шведский математик, брат композитора Сигурда фон Коха.
Родился в 1870 г. в Стокгольме. В 1887-1892 гг. учился в Стокгольмском институте, по завершении которого стал доктором философии и доцентом. В 1905 г. получил звание профессора математики при Технологическом институте, а в 1910 г. стал членом Шведской Академии наук.
Специалист преимущественно по теории чисел.
В статье «Об одной непрерывной кривой, не имеющей касательных...» (фр. Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire; 1904) впервые описал кривую Коха — один из самых ранних и самых известных примеров фрактала.
Кривая Коха и Снежинка Коха
Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом.
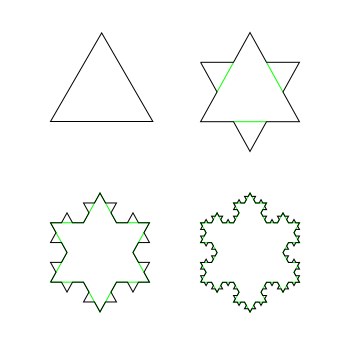
Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую бесконечной длины, называемую снежинкой Коха.
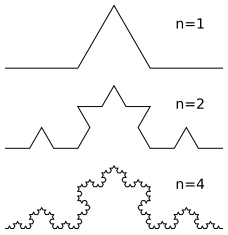
Кривая Коха
Построение
Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.
Свойства
Вариации и обобщения
Возможны обобщения кривой Коха, также использующие при построении подстановку ломаной из четырёх равных отрезков, но имеющей иную геометрию. Они имеют хаусдорфову размерность от 1 до 2. В частности, если вместо деления отрезка 1:1:1 использовать золотое сечение (φ:1:φ ), то получившаяся кривая имеет отношение к мозаикам Пенроуза.
Также можно построить кривую «Крест Коха» на сторонах квадрата, при этом проводя построение «внутрь» квадрата.
Также можно построить «Снежинку Коха» на сторонах равностороннего треугольника.
Вслед за подходом Коха были разработаны варианты с прямыми углами (квадратичная), других углов (Césaro) или кругов и их расширения на высшие размерности (сферическая снежинка).
Я покажу здесь только некоторые вариации. Посмотреть на остальные приглашаю в статью Википедии.

Фрактал Cesaro («Koch Curve 85degrees» участника Alexis Monnerot-Dumaine - Author. Под лицензией CC BY-SA 3.0 с сайта Викисклада)
Фрактал Cesaro — вариант кривой Коха с углом между 60° и 90 ° (здесь 85°).

Поверхность Коха («Koch surface 3» участника Robert Dickau - собственная работа. Под лицензией CC BY-SA 3.0 с сайта Викисклада)
Анимации
читать дальше
Ссылки и картинки
читать дальше

Википедия
Нильс Фабиан Хельге фон Кох (швед. Niels Fabian Helge von Koch, 25 января 1870 — 11 марта 1924) — шведский математик, брат композитора Сигурда фон Коха.
Родился в 1870 г. в Стокгольме. В 1887-1892 гг. учился в Стокгольмском институте, по завершении которого стал доктором философии и доцентом. В 1905 г. получил звание профессора математики при Технологическом институте, а в 1910 г. стал членом Шведской Академии наук.
Специалист преимущественно по теории чисел.
В статье «Об одной непрерывной кривой, не имеющей касательных...» (фр. Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire; 1904) впервые описал кривую Коха — один из самых ранних и самых известных примеров фрактала.
Кривая Коха и Снежинка Коха
Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом.
Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую бесконечной длины, называемую снежинкой Коха.

Кривая Коха
Построение
Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.
Свойства
- Кривая Коха нигде не дифференцируема и не спрямляема.
- Кривая Коха не имеет самопересечений.
- Кривая Коха имеет промежуточную (то есть не целую) хаусдорфову размерность, которая равна `ln4/ln3 approx 1,26` поскольку она состоит из четырёх равных частей, каждая из которых подобна всей кривой с коэффициентом подобия 1/3.
Вариации и обобщения
Возможны обобщения кривой Коха, также использующие при построении подстановку ломаной из четырёх равных отрезков, но имеющей иную геометрию. Они имеют хаусдорфову размерность от 1 до 2. В частности, если вместо деления отрезка 1:1:1 использовать золотое сечение (φ:1:φ ), то получившаяся кривая имеет отношение к мозаикам Пенроуза.
Также можно построить кривую «Крест Коха» на сторонах квадрата, при этом проводя построение «внутрь» квадрата.
Также можно построить «Снежинку Коха» на сторонах равностороннего треугольника.
Вслед за подходом Коха были разработаны варианты с прямыми углами (квадратичная), других углов (Césaro) или кругов и их расширения на высшие размерности (сферическая снежинка).
Я покажу здесь только некоторые вариации. Посмотреть на остальные приглашаю в статью Википедии.

Фрактал Cesaro («Koch Curve 85degrees» участника Alexis Monnerot-Dumaine - Author. Под лицензией CC BY-SA 3.0 с сайта Викисклада)
Фрактал Cesaro — вариант кривой Коха с углом между 60° и 90 ° (здесь 85°).

Поверхность Коха («Koch surface 3» участника Robert Dickau - собственная работа. Под лицензией CC BY-SA 3.0 с сайта Викисклада)
Анимации
читать дальше
Ссылки и картинки
читать дальше







-
-
03.02.2015 в 11:46-
-
03.02.2015 в 18:00