| |
на ... вопрос о том, можно ли по способу Бельтрами осуществить в евклидовом пространстве на некоторой регулярной аналитической поверхности всю плоскость Лобачевского, надо ответить отрицательно
Давид Гильберт. Основания геометрии |
Сегодня отмечается день просветителя. То есть, в некотором роде, и меня )
По этому случаю оглашу сегодняшнего именинника.
Сегодня,
16 ноября, исполнилось
178 лет со дня рождения итальянского математика
Эудженио Бельтрами.

Википедия
Эудженио Бельтрами (итал. Eugenio Beltrami; 16 ноября 1835, Кремона — 18 февраля 1900, Рим) — итальянский математик, известный своими работами по дифференциальной геометрии и математической физике. Сыграл значительную роль в признании неевклидовой геометрии.
1862 — профессор университета в Болонье, преподавал также в Пизе.
1873 — член Национальной Академии деи Линчеи в Риме, с 1898 года — президент Академии.
1873 — профессор университета в Риме.
Основные труды относятся к дифференциальной геометрии, в частности, показал, что геометрия Лобачевского на плоскости локально реализуется на некоторой поверхности в трёхмерном пространстве, называемой псевдосферой или поверхностью Бельтрами, а также установил факт, что любую линейчатую поверхность можно единственным образом изогнуть так, что произвольная линия на ней станет асимптотической (это утверждение известно как теорема Бельтрами). С его именем также связано доказательство свойства асимптотических линий поверхностей отрицательной кривизны, известного как теорема Бельтрами — Эннепера.
Кроме ссылок, это всё, что написано в Википедии. Но мы двинемся чуть дальше.
Сначала разберемся с линейчатыми поверхностями.
Линейчатая поверхностьчитать дальшеВ дифференциальной геометрии, линейчатая поверхность ― поверхность, образованная движением прямой линии. Прямые, принадлежащие этой поверхности, называются прямолинейными образующими, а каждая кривая, пересекающая все прямолинейные образующие, направляющей кривой. Если p(u) ― радиус-вектор направляющей, a m=m(v) ― единичный вектор образующей, проходящей через p(u), то радиус-вектор линейчатой поверхности есть
r=p(u)+vm(u),
где v ― координата точки на образующей.
Свойства
- Линейчатая поверхность характеризуется тем, что ее асимптотическая сеть ― полугеодезическая.
- Гауссова кривизна линейчатой поверхности `K <= 0`.
- Теорема Бельтрами. Линейчатую поверхность всегда можно и притом единственным образом изогнуть так, что произвольная линия на ней станет асимптотической.
- Теорема Бонне. Кроме того, если линейчатая поверхность F, не являющаяся развертывающейся, изгибается в линейчатую поверхность F', то либо их образующие соответствуют друг другу, либо обе они изгибаются в квадрику, на которой сеть, соответствующая семействам образующих, ― асимптотическая.
- Единственная минимальная линейчатая поверхность ― геликоид.

Линейчатый геликоид
- Линейчатая поверхность вращения ― однополостный гиперболоид, быть может вырождающийся в цилиндр, конус или плоскость.


Линейчатый гиперболоид
- Если все прямолинейные образующие линейчатой поверхности параллельны одной плоскости, то она представляет собой поверхность Каталана.
Еще картинки. Гиперболический параболоид
Поверхность Бельтрами (псевдосфера)читать дальшеПсевдосфера (поверхность Бельтрами) — поверхность постоянной отрицательной кривизны, образуемая вращением трактрисы около её асимптоты. Название подчёркивает сходство и различие со сферой, которая является примером поверхности с кривизной, также постоянной, но положительной.


Псевдосфера
Трактриса (линия влечения или линия погони) — (от лат. trahere — тащить) — плоская трансцендентная кривая, для которой длина отрезка касательной от точки касания до точки пересечения с фиксированной прямой является постоянной величиной.
Такую линию описывает предмет, волочащийся на верёвке длины a за точкой, движущейся по оси абсцисс. Трактриса также является кривой погони.

Трактриса
Псевдосфера впервые исследована Миндингом в 1839 — 1840 гг. В частности, им было показано, что понятия группы движений и конгруэнтных фигур имеют смысл лишь на поверхностях постоянной кривизны. Название «псевдосфера» поверхности дал Бельтрами. Он же обратил внимание на то, что псевдосфера реализует локальную модель геометрии Лобачевского, наряду с моделью Пуaнкаре и моделью Клейна.
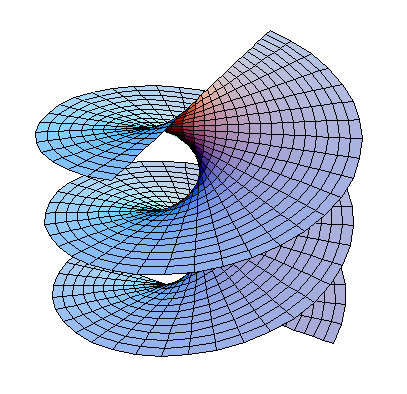
Нашла ссылку на статью "Тороподобные поверхности" П.В. Путенихина. Полистайте! Любопытно.
Тороподобные поверхности







-
-
16.11.2013 в 18:23-
-
16.11.2013 в 18:36Очень красиво.
Немножко не поняла про трактрису.
Такую линию описывает предмет, волочащийся на верёвке длины `a` за точкой, движущейся по оси абсцисс.
Если она уже построена, то да, тогда понятно. Предмет волочится по трактрисе, а другой конец веревки как по рельсу едет по оси абсцисс.
Но если трактрисы нет, как этот предмет будет волочиться, чтобы ее описать? И то не очень понятно. Почему веревка будет касательной?
-
-
16.11.2013 в 18:46-
-
16.11.2013 в 18:54-
-
16.11.2013 в 20:07-
-
16.11.2013 в 20:11..
-
-
16.11.2013 в 20:18-
-
16.11.2013 в 20:25-
-
16.11.2013 в 20:33-
-
16.11.2013 в 20:39-
-
16.11.2013 в 20:48-
-
16.11.2013 в 21:03-
-
16.11.2013 в 21:06-
-
16.11.2013 в 22:28Расположите экран ПК горизонтально
-
-
16.11.2013 в 22:35Гость, вертикально?
Или я не понимаю? Ось Ох вверх?
Всё равно не получится. Его придется сначала быстро, а потом мееедленно вращать. Иначе сначала это груз поедет по горизонтальной оси, а потом по вертикальной...
-
-
16.11.2013 в 22:38-
-
16.11.2013 в 22:38-
-
16.11.2013 в 22:39Гость, вертикально?Или я не понимаю? Ось Ох вверх?
Всё равно не получится. Его придется сначала быстро, а потом мееедленно вращать. Иначе сначала это груз поедет по горизонтальной оси, а потом по вертикальной...
All_ex, спасибо!
Как я вовремя не перелогинилась )) Хоть можно краснеть не от того лица ))
-
-
16.11.2013 в 22:41Если положить монитор и выйти из плоскости, я поняла. А если просто поменять оси, оставшись на плоскости, как я думала, то там резинки не надо - хватит и веревки.
-
-
16.11.2013 в 22:42-
-
16.11.2013 в 22:43