[Amicus Plato]

Каждый знает, что такое кривая, пока не изучит математику настолько, чтобы запутаться в бесчисленном количество всевозможных исключений. Феликс Клейн

Сегодня исполняется 164 года со дня рождения выдающегося немецкого математика и педагога Феликса Клейна.

Википедия.
Феликс Христиан Клейн (нем. Felix Christian Klein; 1849—1925) — немецкий математик и педагог. Член Берлинской академии наук (1913), иностранный член-корреспондент Петербургской академии наук (1895).

Биография
Феликс Клейн родился в Дюссельдорфе, в семье чиновника. Закончил гимназию в Дюссельдорфе, потом учился математике и физике в Боннском университете. Вначале планировал стать физиком. В это время Юлиус Плюккер заведовал отделением математики и экспериментальной физики в Бонне, и Клейн стал его ассистентом. Однако главным интересом Плюккера была геометрия. Под его руководством Клейн стал доктором в 1868 году.
1868: Плюккер умер. Клейн совершает поездку по Германии, знакомится с Клебшем и другими крупными математиками. Особенное влияние на него оказал Софус Ли.
1870: в самое неудачное время (назревает франко-прусская война) вместе с Ли приезжает в Париж, где знакомится с Дарбу и Жорданом. После начала войны возвращается в Германию, где чуть не становится жертвой спутника войны — эпидемии тифа.
1872: профессор Эрлангенского университета, по рекомендации Клебша. Публикует знаменитую «Эрлангенскую программу» и сразу приобретает общеевропейскую известность.
1875: профессор Высшей технической школы в Мюнхене. Женится на Анне Гегель, внучке знаменитого философа.
1876: совместно с Адольфом Майером становится главным редактором журнала «Mathematische Annalen».
1880: переходит в Лейпцигский университет.
1882—1884: серьёзная болезнь по причине переутомления. Клейн переориентирует свою гигантскую энергию на педагогическую и общественную работу.
1888: профессор Гёттингенского университета. Ведёт яркие, глубокие и содержательные факультативные курсы по самым разнообразным предметам, от теории чисел до технической механики. Слушатели его курсов приезжали со всех концов мира.
В начале XX века Клейн принял активное участие в реформе школьного образования, автор и инициатор ряда исследований состояния дел с преподаванием математики в разных странах.
Клейн способствовал созданию при Гёттингенском университете системы научно-исследовательских институтов для прикладных исследований в самых разных технических областях. Участвовал в издании полного собрания сочинений Гаусса и первой Математической энциклопедии. Представлял Гёттингенский университет в парламенте. Надо отметить, что с началом Первой мировой войны Клейн не участвовал в многочисленных тогда шовинистических акциях.
1924: широко отмечается 75-летие Клейна. В следующем году те же газеты опубликовали его некролог.

Раздел про его научную деятельность публиковать не буду. Вместо этого чуть-чуть расскажу про бутылку Клейна и приведу список литературы.

Бутылка Клейна
Бутылка Клейна — это определённая неориентируемая поверхность (то есть двумерное многообразие). Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиуса и проективной плоскостью. Название, по-видимому, происходит от неправильного перевода немецкого слова Fläche (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка); затем это название вернулось в таком виде в немецкий.
Чтобы построить модель бутылки Клейна, понадобится бутылка с двумя дополнительными отверстиями: в донышке и в стенке. Горлышко бутылки нужно вытянуть, изогнуть вниз, и продев его через отверстие в стенке, присоединить к отверстию на дне бутылки. Для настоящей бутылки Клейна в четырёхмерном пространстве отверстие в стенке не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве.

В отличие от обыкновенного стакана у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу не пересекая поверхность (то есть на самом деле у этого объекта нет «внутри» и нет «снаружи»).
Бутылка Клейна, погруженная в трехмерное пространство:

Свойства

• Подобно ленте Мёбиуса, бутылка Клейна является двумерным дифференцируемым неориентируемым многообразием. В отличие от ленты Мёбиуса, бутылка Клейна является замкнутым многообразием, то есть компактным многообразием без края.
• Бутылка Клейна не может быть вложена (только погружена) в трёхмерное евклидово пространство `RR^3`, но вкладывается в `RR^4`.
• Бутылка Клейна может быть получена склеиванием двух лент Мёбиуса по краю. Однако в обычном трехмерном евклидовом пространстве `RR^3` сделать это, не создав самопересечения, невозможно.
• Хроматическое число поверхности равно 6.

Рассечения
При рассечении бутылки Клейна получается лента Мёбиуса.
Если разрезать бутылку Клейна пополам вдоль её оси симметрии, то результатом будет лента Мёбиуса, изображенная внизу (необходимо помнить, что изображенного пересечения на самом деле нет).

Реализация бутылки Клейна в виде восьмерки:

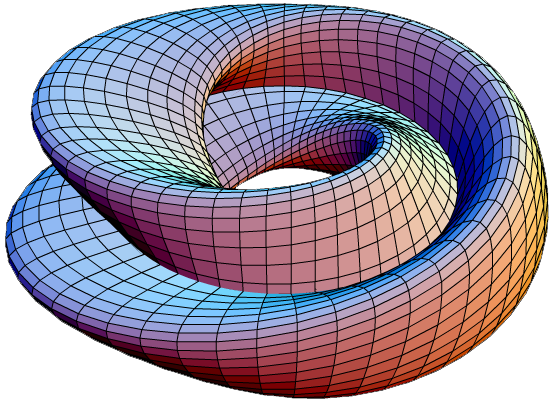
Стеклянная бутылка Клейна:

Больше картинок (и все очень хороши!) в английской Википедии: en.wikipedia.org/wiki/Klein_bottle

Ссылки на литературу.
1. Яглом И.М. Феликс Клейн и Софус Ли. 1977 libgen.info
2. Книги Ф. Клейна libgen.info:
Клейн Ф. Элементарная математика с точки зрения высшей том 1 1987
Клейн Ф. Элементарная математика с точки зрения высшей том 2 1987
Клейн Ф. Лекции об икосаэдре и решении уравнений пятой степени 1989
Клейн Ф. Высшая геометрия 2004
Клейн Ф. Неевклидова геометрия 1936
Клейн Ф. Лекции о развитии математики в XIX столетии часть 1 1937
Клейн Ф. Вопросы элементарной и высшей математики. Арифметика, алгебра и анализ Часть 1 1912

@темы: История математики, Люди

Comments

[All_ex]

Amicus Plato и снова, спасибо!...
Больше картинок (и все очень хороши!) в английской Википедии: - вторя стеклянная бутылка очень смахивает на самогонный аппарат...

[Груша Вильямс]

Спасибо!
Я бы купил такую, кувшин для воды, компота

[Amicus Plato]

All_ex,

вторя стеклянная бутылка очень смахивает на самогонный аппарат...

Ага! Но мне там кроме самогонного аппарата понравился наглядный принцип ее построения. Помню, как мучился наш лектор, рисуя это на доске ))

Груша Вильямс,

Я бы купил такую, кувшин для воды, компота

Боюсь, это безнадежная затея иметь в качестве емкости для жидкости неориентируемую поверхность))

[Amicus Plato]

Вот еще по части картинок:
en.wikipedia.org/wiki/Orientability

[~ghost]

Amicus Plato, Спасибо !
бутылки "симпатичные"..=) и интересные..

[VEk]

Спасибо!