Простыми словами
Сегодня исполняется 160 лет со дня рождения выдающегося итальянского математика, создателя тензорного исчисления Грегорио Риччи-Курбастро.

Википедия
Грегорио Риччи-Курбастро (итал. Gregorio Ricci-Curbastro; 12 января 1853, Луго — 6 августа 1925, Болонья) — итальянский математик.
С 1880 г. — профессор в университете в Падуе. Его важная научная заслуга заключается в создании «абсолютного дифференциального исчисления» (тензорного исчисления), широко используемого в общей теории относительности, дифференциальной геометрии, теории многообразий и т. д.
Наряду с Риччи в этом признается фундаментальный вклад Римана, Кристоффеля и ученика Риччи Леви-Чивиты.
Тензор Риччи
Тензор Риччи, названный в честь Риччи-Курбастро, задаёт один из способов измерения кривизны многообразия, то есть степени отличия геометрии многообразия от геометрии плоского евклидова пространства. Тензор Риччи, точно так же как метрический тензор, есть симметричная билинейная форма на касательном пространстве риманова многообразия. Грубо говоря, тензор Риччи измеряет деформацию объёма, то есть степень отличия n-мерных областей n-мерного многообразия от аналогичных областей евклидова пространства.
Геометрический смысл тензора Риччи
В окрестности любой точки `p` риманова многообразия `(M, g)` можно всегда определить специальные локальные координаты, так называемые нормальные геодезические координаты, в которых геодезические из точки p совпадают с прямыми, проходящими через начало координат. Кроме того, в самой точке `p` метрический тензор равен метрике евклидова пространства `delta_(ij)` (или метрике Минковского `eta_(ij)` в случае псевдориманова многообразия).
В этих специальных координатах форма объема раскладывается в ряд Тейлора вокруг `p`:
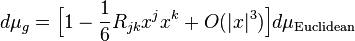
Таким образом, если кривизна Риччи `Ric(xi,xi)` положительна в направлении вектора `xi`, то узкий конус геодезических, исходящих из точки `p` в направлении `xi`, будет иметь меньший объем, чем такой же конус в евклидовом пространстве. Аналогично, если кривизна Риччи отрицательна, то узкий конус геодезических в направлении вектора `xi` будет иметь объем, больший по сравнению с евклидовым.
А вот пространство Калаби — Яу, имеющее нулевой тензор Риччи
Пространство Калаби — Яу и теория струн

Википедия
Грегорио Риччи-Курбастро (итал. Gregorio Ricci-Curbastro; 12 января 1853, Луго — 6 августа 1925, Болонья) — итальянский математик.
С 1880 г. — профессор в университете в Падуе. Его важная научная заслуга заключается в создании «абсолютного дифференциального исчисления» (тензорного исчисления), широко используемого в общей теории относительности, дифференциальной геометрии, теории многообразий и т. д.
Наряду с Риччи в этом признается фундаментальный вклад Римана, Кристоффеля и ученика Риччи Леви-Чивиты.
Тензор Риччи
Тензор Риччи, названный в честь Риччи-Курбастро, задаёт один из способов измерения кривизны многообразия, то есть степени отличия геометрии многообразия от геометрии плоского евклидова пространства. Тензор Риччи, точно так же как метрический тензор, есть симметричная билинейная форма на касательном пространстве риманова многообразия. Грубо говоря, тензор Риччи измеряет деформацию объёма, то есть степень отличия n-мерных областей n-мерного многообразия от аналогичных областей евклидова пространства.
Геометрический смысл тензора Риччи
В окрестности любой точки `p` риманова многообразия `(M, g)` можно всегда определить специальные локальные координаты, так называемые нормальные геодезические координаты, в которых геодезические из точки p совпадают с прямыми, проходящими через начало координат. Кроме того, в самой точке `p` метрический тензор равен метрике евклидова пространства `delta_(ij)` (или метрике Минковского `eta_(ij)` в случае псевдориманова многообразия).
В этих специальных координатах форма объема раскладывается в ряд Тейлора вокруг `p`:
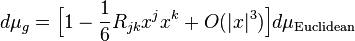
Таким образом, если кривизна Риччи `Ric(xi,xi)` положительна в направлении вектора `xi`, то узкий конус геодезических, исходящих из точки `p` в направлении `xi`, будет иметь меньший объем, чем такой же конус в евклидовом пространстве. Аналогично, если кривизна Риччи отрицательна, то узкий конус геодезических в направлении вектора `xi` будет иметь объем, больший по сравнению с евклидовым.
А вот пространство Калаби — Яу, имеющее нулевой тензор Риччи
Пространство Калаби — Яу и теория струн


-
-
12.01.2013 в 23:45