[Amicus Plato]

Нельзя быть настоящим математиком, не будучи немного поэтом. К. Вейерштрасс

Сегодня исполняется 197 лет со дня рождения Карла Вейерштрасса.
Наверное, представлять его никому не нужно! (Особенно актуально это имя сейчас, я думаю, для первокурсников.)


Википедия пишет о нем вот что.
Карл Теодор Вильгельм Вейерштрасс (нем. Karl Theodor Wilhelm Weierstraß; 31 октября 1815 — 19 февраля 1897) — выдающийся немецкий математик, «отец современного анализа».

Вообще, почему-то сведения о нем в интернете довольно скудны. Не могу сказать, что нет совсем уж ничего, но с учетом того, какой вклад он внес в развитие математики, а также того, какие у него были ученики, могло бы быть и больше.
Так, например, для эпиграфа я предпочла бы другую цитату, но другой не нашлось. Везде только эта!
Но уж что есть...

Под руками у меня книга Д.Я. Стройка "Краткий очерк истории математики". Возьму цитату оттуда.
"В основном это заслуга найчной деятельности Вейерштрасса, что теперь в анализе существуют полное согласие и уверенность относительно таких способов рассуждения, которые основаны на понятии иррационального числа и предела вообще, и ему мы обязаны тем, что существует единодушие относительно всех результатов, даже в наиболее сложных вопросах, касающихся теории дифференциальных и интегральных уравнений, — несмотря на самые дерзновенные и разнообразные сочетания при применении наложения, комбинации и перестановки пределов".
Давид Гильберт

Несколько фактов биографии.

1854: публикует статью по абелевым функциям, за которую Кёнигсбергский университет сразу присуждает ему степень доктора honoris causa (почётного доктора без защиты диссертации). Дирихле присылает восторженный отзыв, благодаря которому Вейерштрасс получает звание старшего учителя и давно просимый годичный отпуск.
Отдых он использовал для подготовки ещё одной блестящей статьи (1856). Александр фон Гумбольдт и Куммер помогли Вейерштрассу устроиться профессором сначала Промышленного Института в Берлине, а через пару месяцев — экстраординарным профессором Берлинского университета. Одновременно он избран членом Берлинской Академии наук. Берлинскому университету он отдал 40 лет жизни.
С конца 1850-х годов международная известность Вейерштрасса быстро растёт. Этим он обязан великолепному качеству своих лекций. Вот список тематики его курсов:

• Введение в теорию аналитических функций, включающее теорию действительных чисел.
• Теория эллиптических функций, приложения эллиптических функций к задачам геометрии и механики.
• Теория абелевых интегралов и функций.
• Вариационное исчисление.

Здоровье Вейерштрасса оставляет желать лучшего — сказывается постоянное переутомление в молодые годы. В 1861 году во время выступления у него начался сильный приступ головокружения. и пришлось прервать лекцию. Больше Вейерштрасс никогда не читал лекции стоя — он неизменно сидел, а один из лучших студентов писал за него на доске.

Факты биографии и не только

А вот, что пишет Википедия, а затем тиражируют все биографические сайты.

1.
В 1870 Вейерштрасс знакомится с двадцатилетней Софьей Ковалевской, приехавшей в Берлин для подготовки диссертации. Нежное чувство к своей Sonja Вейерштрасс пронёс сквозь всю жизнь (он так и не женился). Вейерштрасс помогает Ковалевской выбрать тему диссертации и метод подхода к решению, в дальнейшем регулярно консультирует её по сложным вопросам анализа, содействует в получении научного признания.
После защиты диссертации Ковалевская уехала, на письма учителя отвечала редко и неохотно, за исключением ситуаций, когда ей срочно требовалась консультация.

2.
В 1883-м после самоубийства мужа Ковалевская, оставшаяся без средств с пятилетней дочерью, приезжает в Берлин и останавливается у Вейерштрасса. Ценой огромных усилий, используя весь свой авторитет и связи, Вейерштрассу удаётся выхлопотать ей место профессора в Стокгольмском университете.

Как-то стыдновато за Софью Васильевну, хоть жизнь у нее, понятно, тоже была не сахар.

Еще один примечательный факт. Везде пишут, что Вейерштрасс обладал незаурядным педагогическим даром, и в числе его учеников множество замечательных ученых. Неполный перечень таков: Э. Гуссерль, Ф. Л. Зейдель, Г. Кантор, С. В. Ковалевская, М. Г. Миттаг-Леффлер, Ф. Г. Фробениус, К. Г. А. Шварц.
Хочу остановиться на Миттаг-Леффлере. Посмотрите, какой красавец.

Сразу по нескольким версиям именно из-за него Нобель отказался учреждать премию по математике. Вроде бы Миттаг-Леффлер был его счастливым соперником. Хотя некоторые утверждают обратное или даже нечто третье...

Но вернемся к Вейерштрассу.

Научная деятельность

Научная деятельность (Материал из Википедии)
Исследования Вейерштрасса существенно обогатили математический анализ, теорию специальных функций, вариационное исчисление, дифференциальную геометрию и линейную алгебру. В математике Вейерштрасс стремился к ясности и строгости. Пуанкаре писал о нём: «Вейерштрасс отказывается пользоваться интуицией или по крайней мере оставляет ей только ту часть, которую не может у нее отнять».
До Вейерштрасса оснований анализа фактически не существовало. Даже Коши, который впервые ввёл стандарты строгости, многое молчаливо подразумевал. Не было теории вещественных чисел — превосходная статья Больцано (1817) осталась незамеченной. Важнейшее понятие непрерывности использовалось без какого-либо определения. Отсутствовала полная теория сходимости. Как следствие, немало теорем содержали ошибки, нечёткие или чрезмерно широкие формулировки.

Вейерштрасс завершил построение фундамента математического анализа, прояснил тёмные места, построил ряд доказательных контрпримеров (аномальных функций), например, всюду непрерывную, но нигде не дифференцируемую функцию.
Он сформулировал логическое обоснование анализа на основе построенной им теории действительных (вещественных) чисел и так называемого ε-δ-языка.

Непрерывная нигде не дифференцируемая функция

вот:

вот:

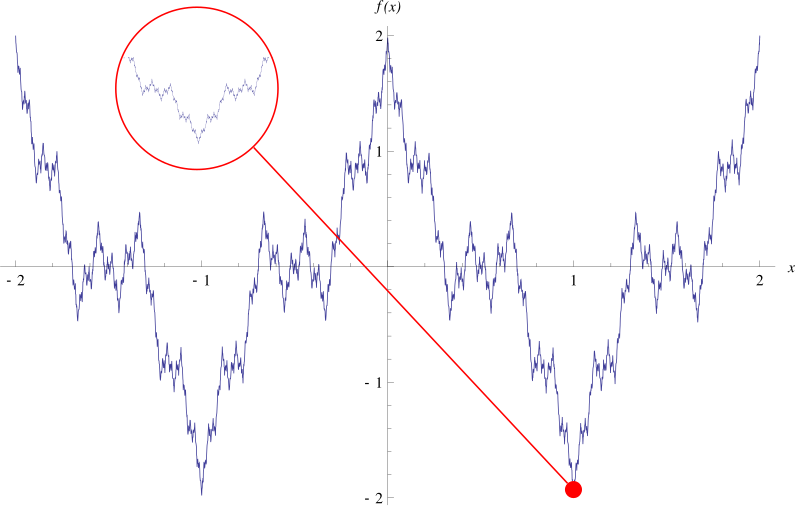
График функции Вейерштрасса на интервале [−2, 2]. Этот график имеет фрактальный характер, демонстрируя самоподобие: увеличиваемая область (в красном круге) подобна всему графику.

Одновременно он дал строгое доказательство основных свойств непрерывных функций. Приведенное определение, а также его определения предела, сходимости ряда и равномерной сходимости функций воспроизводятся без всяких изменений в современных учебниках.
Вейерштрасс систематически использовал понятия верхней и нижней грани и предельной точки числовых множеств.
Вейерштрасс доказал, что любая непрерывная функция допускает представление равномерно сходящимся рядом многочленов. Он далеко продвинул теорию эллиптических и абелевых функций, заложил основы теории целых функций и функций нескольких комплексных переменных. Создал теорию делимости степенных рядов.
Вариационное исчисление Вейерштрасс также преобразовал, придав его основаниям современный вид. Он открыл условия сильного экстремума и достаточные условия экстремума, исследовал разрывные решения классических уравнений.
В геометрии он создал теорию минимальных поверхностей, внёс вклад в теорию геодезических линий.
В линейной алгебре им разработана теория элементарных делителей.
Вейерштрасс доказал, что поле комплексных чисел — единственное коммутативное расширение поля действительных чисел без делителей нуля (1872).

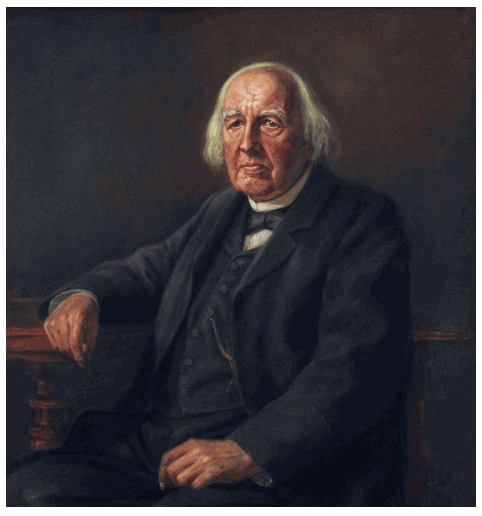
О публикациях своих выдающихся лекций сам Вейерштрасс не заботился. Однако ещё при жизни начало выходить собрание его трудов; всего вышло 7 томов (последний — в 1927 г.).

Ну и как всегда в завершении бонус.
Правда, в этот раз он получился несколько... эээ... Судите сами

Бонус

Азбука для самых маленьких "Учим алфавит с Демидовичем", буква "А" - Аппроксимационная теорема Вейерштрасса

отсюда

И еще один портрет.

Украинский Вейерштрасс. Хотя страничка, откуда я это взяла, называется Mathematicians_rus: вот.

@темы: История математики, Люди

Comments

[к.черный]

Как-то стыдновато за Софью Васильевну

за непоследовательность?

Ой, спасибо, конечно, за материал. Как всегда, кругозорорасширяюще

[All_ex]

Amicus Plato, спасибо....
Если брать бонус, то понятно, что вопрос уже не к Вам... Что на картинке с "Аппроксимационной теоремой Вейерштрасса" означает запись `lim_{k=0} ...`? Может там должно быть `k to 0`?... Вот так и учат с младых ногтей ...

[Amicus Plato]

за непоследовательность?

к.черный,
За черную неблагодарность! ((
Ну а потом уже и за непоследовательность, конечно. )

Стыдно скорее не за нее, а вместо нее.

All_ex, я и сказала, что картинка сомнительна (( Но идея хороша! Надо будет перерисовать при случае.
Правда, как я поняла, на букве А у них алфавит и закончился.

С Днем Рождения такого замечательного товарища!

[Amicus Plato]

И вообще, там должны быть многочлены `p(x)`...

===
UPD. Нашла! Это в Википедии такой предел написан
ru.wikipedia.org/wiki/%D0%90%D0%BF%D0%BF%D1%80%...

[Amicus Plato]

Avis Alba, и вас также! )

[All_ex]

UPD. Нашла! Это в Википедии такой предел написан - Ну, в Вики есть кнопка "править"... а тут нема...

Правда, как я поняла, на букве А у них алфавит и закончился. - Так можно продолжить...
"Б" - булева функция...
"В" - всюду плотное множество..
...

[Amicus Plato]

All_ex,

"Б" - булева функция...
"В" - всюду плотное множество..
...

Можно взяться небольшим авторским коллективом )
С картинками )
"Г" - гауссово распределение
"Д" - Дзета-функция Римана
...

[~ghost]

Amicus Plato, спасибо! )

[All_ex]

Так, например, для эпиграфа я предпочла бы другую цитату, но другой не нашлось. Везде только эта! ...

"Конечная цель, которую всегда нужно иметь в виду, состоит в том, чтобы достичь правильной точки зрения на основания... Но чтобы добиться какого-нибудь прогресса в науках, безусловно, необходимо заниматься отдельными проблемами"
К. Вейерштрасс

"На вопрос... можно ли действительно получить что-либо непосредственно применимое из тех абстрактных теорий, которыми предпочтительно занимаются теперешние математики, я могу ответить, что греческие математики изучили свойства конических сечений чисто умозрительным путем задолго до того, как кто-либо мог предугадать, что эти кривые представляют собой пути, по которым движутся планеты, и я верю, что будет найдено еще много функций с такими свойствами, как, например, знаменитые тэта-функции Якоби, с помощью которых можно, с одной стороны, узнать, на сколько квадратов разлагается любое заданное число, что позволяет спрямить дугу эллипса, и, с другой стороны, как я здесь добавлю, дает возможность найти истинный закон колебаний маятника"
К. Вейерштрасс

И вторя приведённому эпиграфу...
Тот, кто изучал труды таких ученых, как Эйлер, Лагранж, Коши, Риман, Софус Ли и Вейерштрасс, может ли сомневаться, что великий математик - это и великий художник? Одаренность этих людей, характер и степень которой столь отличны у каждого из них, аналогична способностям, необходимым в творческом искусстве. Не каждый математик обладает надлежащим образом развитым критическим талантом, выражающимся в безупречности формы, в согласовании с идеалом логической завершенности; по каждый великий математик обладает редким талантом творческого воображения
Э. У. Гобсон

[All_ex]

Что-то я сидел и тормозил... не мог не как вспомнить что-нибудь простенького для детского алфавита на букву "Е"...

"Е" - евклидово пространство...
"Ж" - жорданова форма матрицы...
"З" - закон больших чисел...
"И" - интегральная формула Коши...
"Й" - йо-моё... (это такая средне статистическая реакция на этот букварь...)

[Amicus Plato]

"Й" - йо-моё...

Это было на "Ё", которое Вы пропустили)))
А на Й есть вполне себе Йота-оператор Россера-Тюркетта ))

[v-sofie]

У меня любимые математики (в смысле личности и человечности, а не в клада в науку) - Эйлер и Келдыш, но Вейерштрасс тоже очень удивил, раньше не попадала на его биографию. Очень крутой, и очень интересная вскользь описанная биография Софьи.